Comment générer une distribution normale en Python (avec exemples)

Vous pouvez générer rapidement unedistribution normale en Python en utilisant la fonction numpy.random.normal() , qui utilise la syntaxe suivante :

numpy.random.normal(loc=0.0, scale=1.0, size=None)

où:

• loc : Moyenne de la distribution. La valeur par défaut est 0.
• échelle : Écart type de la distribution. La valeur par défaut est 1.
• taille : taille de l’échantillon.

Ce didacticiel montre un exemple d’utilisation de cette fonction pour générer une distribution normale en Python.

Connexe :Comment créer une courbe en cloche en Python

Exemple : générer une distribution normale en Python

Le code suivant montre comment générer une distribution normale en Python :

from numpy.random import seed
from numpy.random import normal

#make this example reproducible
seed(1)

#generate sample of 200 values that follow a normal distribution 
data = normal(loc=0, scale=1, size=200)

#view first six values
data[0:5]

array([ 1.62434536, -0.61175641, -0.52817175, -1.07296862,  0.86540763])

On peut trouver rapidement la moyenne et l’écart type de cette distribution :

import numpy as np

#find mean of sample
np.mean(data)

0.1066888148479486

#find standard deviation of sample
np.std(data, ddof=1)

0.9123296653173484

Nous pouvons également créer un histogramme rapide pour visualiser la distribution des valeurs des données :

import matplotlib.pyplot as plt
count, bins, ignored = plt.hist(data, 30)
plt.show()

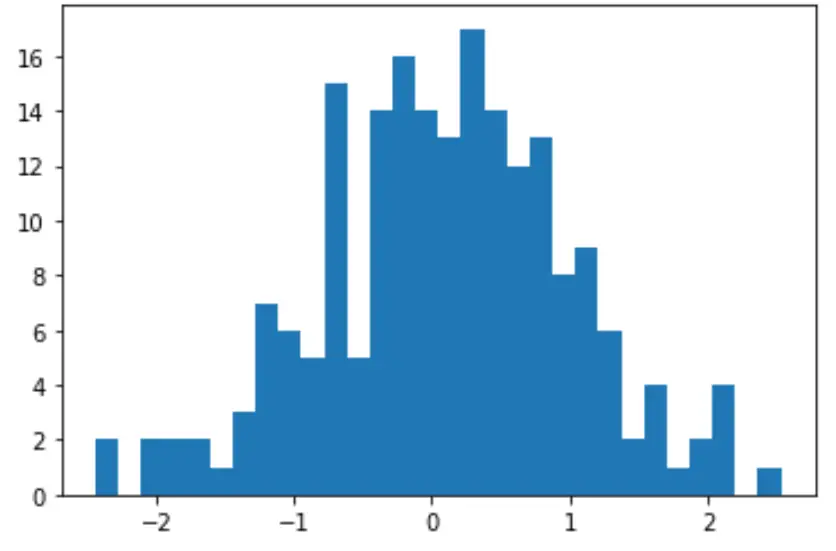
Nous pouvons même effectuer un test de Shapiro-Wilk pour voir si l’ensemble de données provient d’une population normale :

from scipy.stats import shapiro

#perform Shapiro-Wilk test
shapiro(data)

ShapiroResult(statistic=0.9958659410, pvalue=0.8669294714)

La valeur p du test s’avère être de 0,8669 . Puisque cette valeur n’est pas inférieure à 0,05, nous pouvons supposer que les données de l’échantillon proviennent d’une population normalement distribuée.

Ce résultat ne devrait pas être surprenant puisque nous avons généré les données à l’aide de la fonction numpy.random.normal() , qui génère un échantillon aléatoire de données provenant d’une distribution normale.