Graphique en aires

Cet article montre ce que sont les graphiques en aires et des exemples de ce type de diagrammes statistiques. Vous y découvrirez les différents types de graphiques en aires et quels sont leurs avantages et inconvénients.

Qu’est-ce qu’un graphique à aires ?

Un graphique en aires est un type de diagramme statistique dans lequel les données sont représentées par des points reliés par des lignes droites et la zone sous le graphique est colorée.

En d’autres termes, un graphique en aires est comme un polygone de fréquence mais, en plus, la zone située en dessous est peinte.

En statistiques, ces types de graphiques sont principalement utilisés pour montrer l’évolution d’une série temporelle.

Types de graphiques en aires

Il existe trois types de graphiques en aires, qui sont les suivants :

• Tracé de zone simple – Un seul ensemble de données est représenté.
• Graphique à zones multiples – Plusieurs séries de données sont tracées.
• Tracé de zone empilée – Le tracé est composé de plusieurs séries chronologiques, mais elles sont empilées les unes sur les autres.

Chaque type de parcelle de zone est expliqué plus en détail ci-dessous.

Graphique en aires simples

Pour représenter un ensemble de données dans un graphique à aires, les étapes suivantes doivent être effectuées :

1. Dessinez l’axe horizontal et l’axe vertical du diagramme pour pouvoir ensuite représenter les données sur le graphique.
2. Représentez les paires de données sous forme de points sur le graphique.
3. Joignez les points consécutifs sur le graphique avec une ligne.
4. Colorez la zone entre la ligne du graphique et l’axe horizontal.

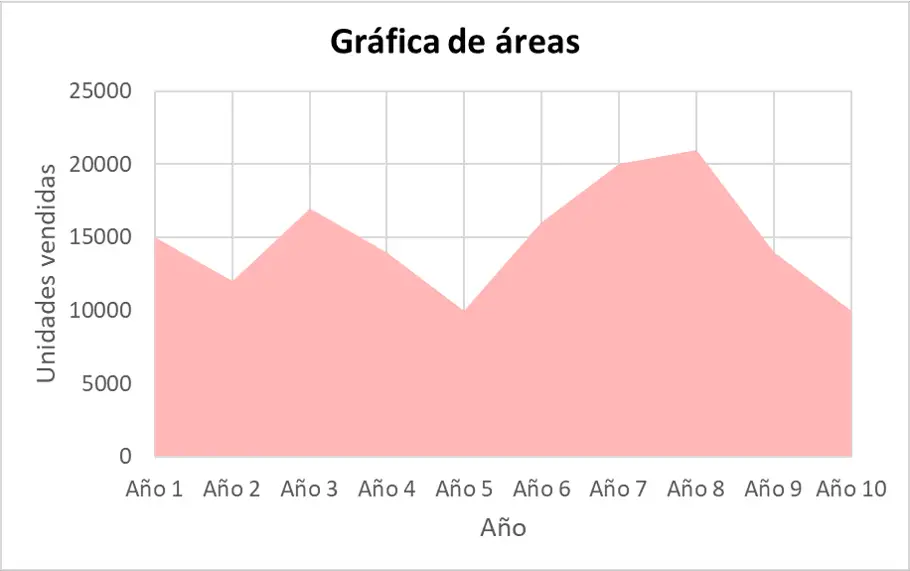
Graphique à zones multiples

Le graphique à zones multiples consiste à représenter deux ou plusieurs ensembles de données différents sur un seul diagramme. De cette manière, les valeurs des séries de données peuvent être comparées.

Le processus de création d’un graphique à aires multiples est le même que pour un graphique à aires uniques, mais le processus doit être effectué plusieurs fois, une fois pour chaque série de données.

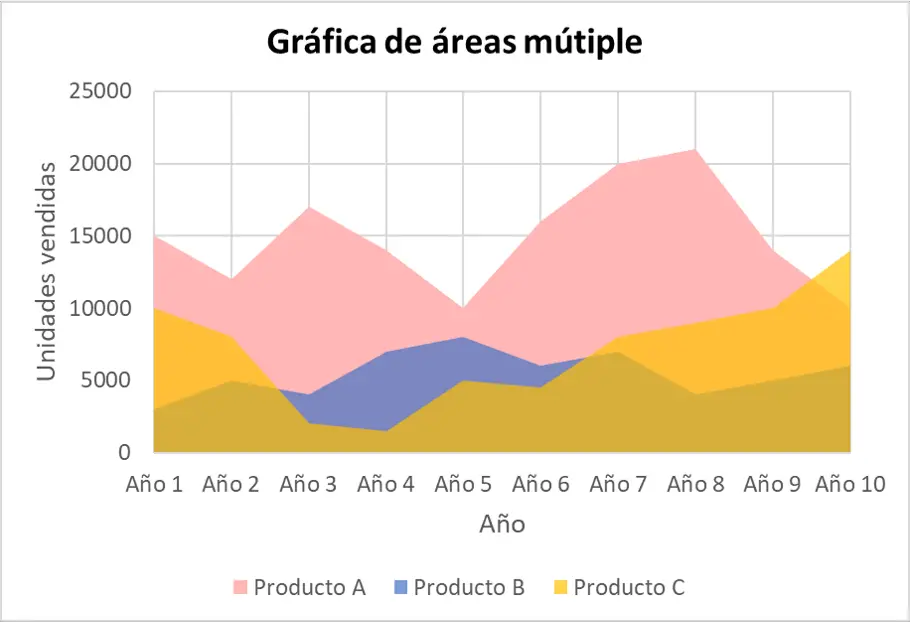
Il est important de peindre les graphiques de différentes couleurs pour pouvoir distinguer facilement les séries. De plus, vous devez ajouter une légende pour indiquer la signification de chaque couleur.

Graphique à aires empilées

Le graphique en aires empilées est basé sur la représentation de plusieurs séries de données dans le même diagramme, mais chaque série est placée au-dessus de la précédente, de sorte qu’aucune série n’en chevauche une autre.

L’exemple suivant a tracé les mêmes données que celles utilisées pour l’exemple de graphique à aires multiples ci-dessus, afin que vous puissiez voir la différence.

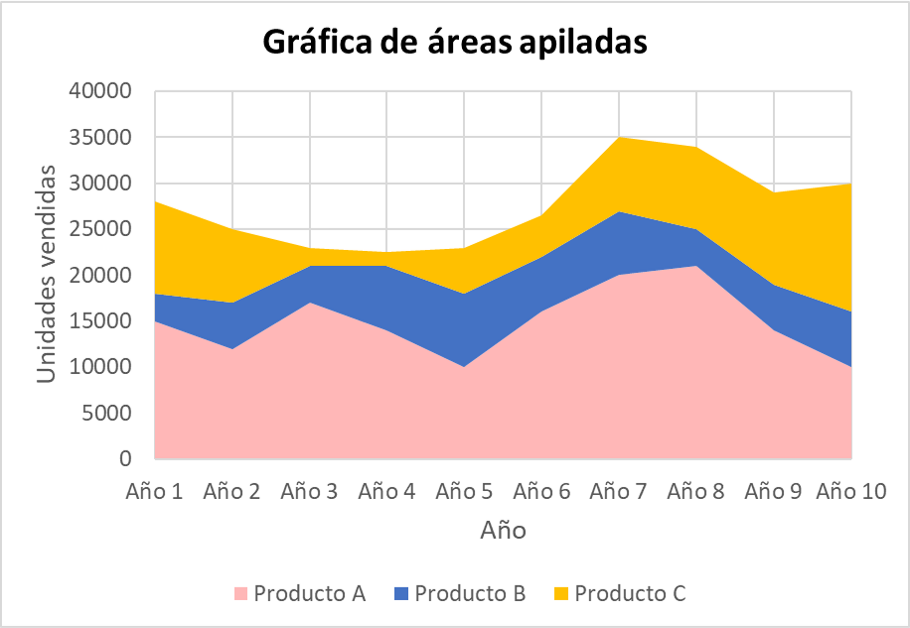
Ce type de diagramme permet de connaître la valeur totale et la contribution de chaque série au total.

Avantages et inconvénients du graphique à aires

En raison de leurs caractéristiques, les graphiques en aires présentent les avantages et les inconvénients suivants :

Avantage:

• Très utile pour représenter graphiquement des séries temporelles par exemple, il permet de représenter la progression des KPI (indicateurs de qualité).
• Il s’agit d’un type de graphique statistique facile à comprendre et à analyser.
• Il permet de comparer différents ensembles de données dans le même graphique.

Désavantages:

• Lorsque de nombreuses séries de données sont représentées graphiquement et non empilées, le graphique est difficile à lire et à comprendre.
• Normalement, les valeurs exactes de la série sont inconnues.

Quand utiliser un graphique en aires

En résumé, nous allons voir quand un graphique en aires doit être utilisé pour représenter les données dans un diagramme.

Les graphiques en aires sont très utiles pour montrer la progression dans le temps. Ils doivent donc être utilisés pour représenter graphiquement une série chronologique.

De plus, ils sont particulièrement pratiques pour représenter différentes séries temporelles qui contribuent à un total sur un même graphique. De cette façon, non seulement vous pouvez comparer les valeurs des différentes séries, mais vous pouvez également connaître le total, c’est-à-dire la somme de toutes les valeurs.