Histogramme

Cet article explique en quoi consiste un histogramme, à quoi il sert et comment interpréter un histogramme. Ainsi, vous découvrirez comment réaliser un histogramme et des exemples de tous types d’histogrammes.

Qu’est-ce qu’un histogramme ?

Un histogramme est un type de diagramme statistique dans lequel un ensemble de données statistiques est représenté par des barres rectangulaires, de sorte que chaque barre de l’histogramme soit proportionnelle à sa fréquence correspondante.

Les histogrammes sont utilisés pour représenter graphiquement des variables continues, telles que le poids d’un échantillon statistique. De plus, un histogramme permet de visualiser rapidement la forme d’une distribution.

Chaque barre d’un histogramme de fréquence a une largeur proportionnelle à la largeur de l’intervalle et une hauteur proportionnelle à la fréquence de l’intervalle.

Comment faire un histogramme

Les étapes pour créer un histogramme sont :

1. Divisez l’axe horizontal de l’histogramme en groupes en fonction de la série de données.
2. Tracez les valeurs de fréquence d’intervalle sur l’axe vertical de l’histogramme.
3. Pour chaque intervalle, tracez une barre rectangulaire d’une hauteur égale à la fréquence de l’intervalle. Notez que les barres de deux intervalles consécutifs doivent se toucher.

exemple d’histogramme

Une fois que vous avez vu la définition d’un histogramme et la théorie associée, vous pouvez voir ci-dessous un exemple expliqué de la façon dont un graphique statistique de ce type est réalisé.

• Un magasin de vêtements a vendu 50 unités de prix différents au cours d’une journée, comme indiqué dans le tableau de fréquence suivant. Construisez un histogramme à partir des données enregistrées des ventes réalisées.

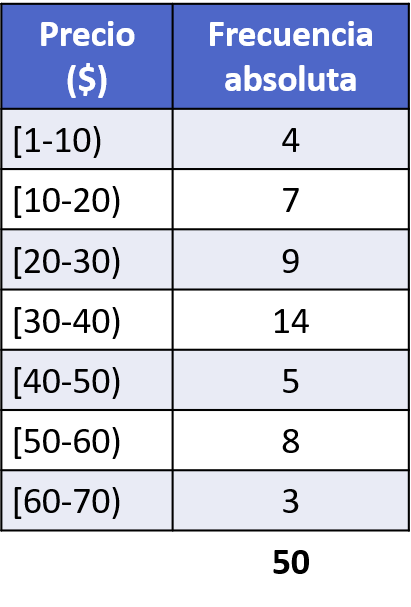
Pour représenter un histogramme, nous devons suivre les étapes expliquées ci-dessus. C’est-à-dire que nous divisons d’abord l’axe horizontal en parties équivalentes aux intervalles des données, puis nous graduons l’échelle de l’axe vertical et, enfin, nous représentons chaque intervalle par une colonne de hauteur égale à sa fréquence absolue.

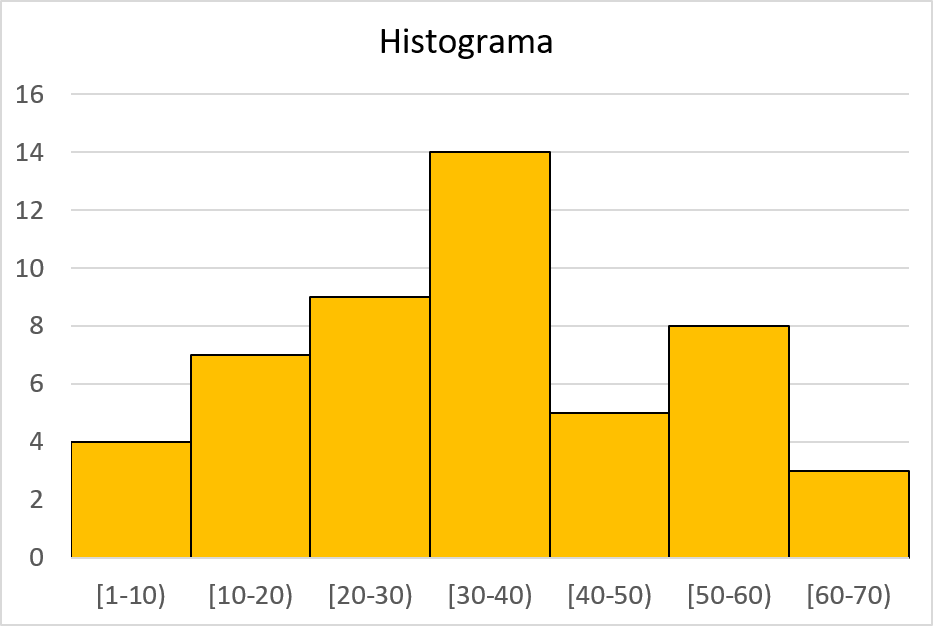
Histogramme de fréquence relative

L’ histogramme des fréquences relatives est un type d’histogramme dans lequel les fréquences relatives de l’ensemble de données sont représentées. Autrement dit, au lieu de représenter graphiquement les fréquences absolues, les fréquences relatives sont représentées.

Bien que différentes fréquences soient représentées, la forme d’un histogramme de fréquence relative est la même que celle d’un histogramme de fréquence absolue, elles changent simplement les valeurs sur l’axe vertical.

A titre d’exemple, nous construirons l’histogramme de fréquence relative à partir de l’étude statistique de l’exercice précédent. Pour ce faire, il faut d’abord calculer la fréquence relative de chaque intervalle, qui équivaut à sa fréquence absolue divisée par le nombre total de données (50).

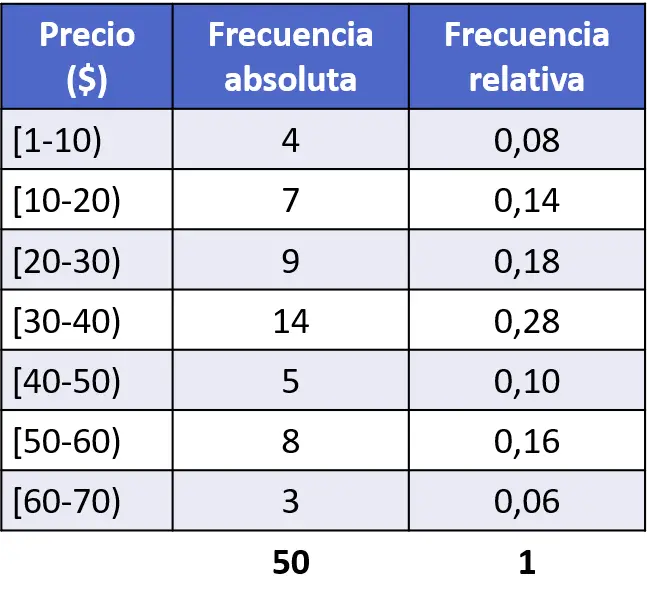
Une fois que nous avons calculé les fréquences relatives, il suffit de les représenter graphiquement dans un histogramme. Pour ce faire, on trace l’axe horizontal, qui correspond aux prix des unités vendues, puis l’axe vertical, dans lequel sont représentées les fréquences relatives, et enfin, pour chaque intervalle une barre rectangulaire d’une hauteur équivalente à sa fréquence relative. fréquence.

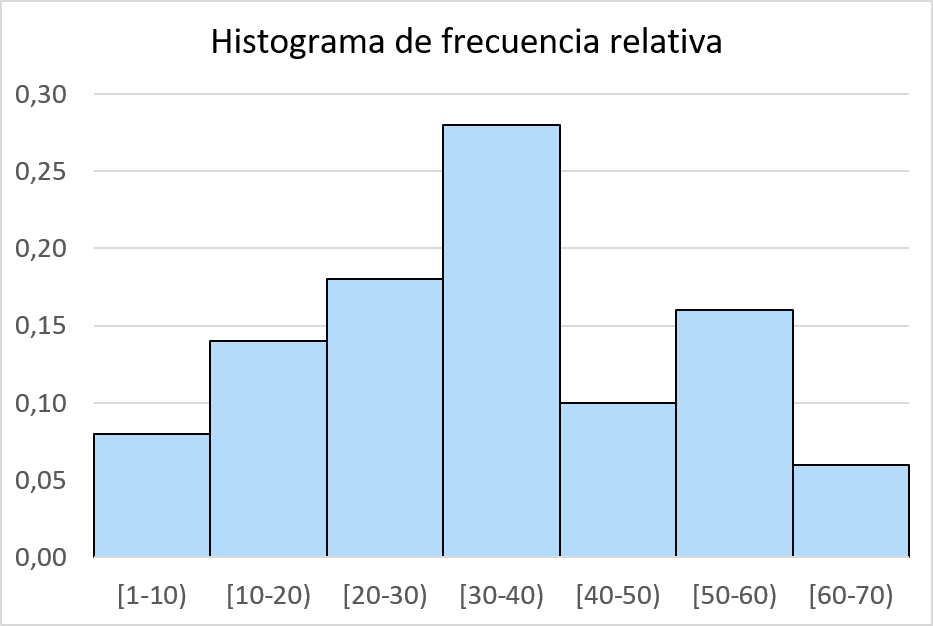
Histogramme de fréquence cumulée

Nous venons de voir comment construire un histogramme de fréquence absolue et un histogramme de fréquence relative, cependant, les histogrammes de fréquence cumulée sont également utilisés en statistiques.

Un histogramme de fréquence cumulée est un type d’histogramme dans lequel les fréquences cumulées sont tracées. Autrement dit, dans un histogramme de fréquence cumulée, les fréquences cumulées sont représentées au lieu des fréquences absolues.

Logiquement, un histogramme de fréquence cumulée peut être réalisé avec des fréquences absolues et relatives. A titre d’exemple, ces deux types d’histogrammes seront représentés ci-dessous en utilisant les mêmes données que l’exercice que nous faisons tout au long de cet article.

Histogramme des fréquences absolues cumulées

Évidemment, pour tracer un histogramme des fréquences absolues cumulées, nous devons d’abord déterminer les fréquences absolues cumulées pour chaque intervalle. Pour ce faire, on additionne toutes les fréquences absolues précédentes à chaque intervalle plus la fréquence absolue de l’intervalle en question :

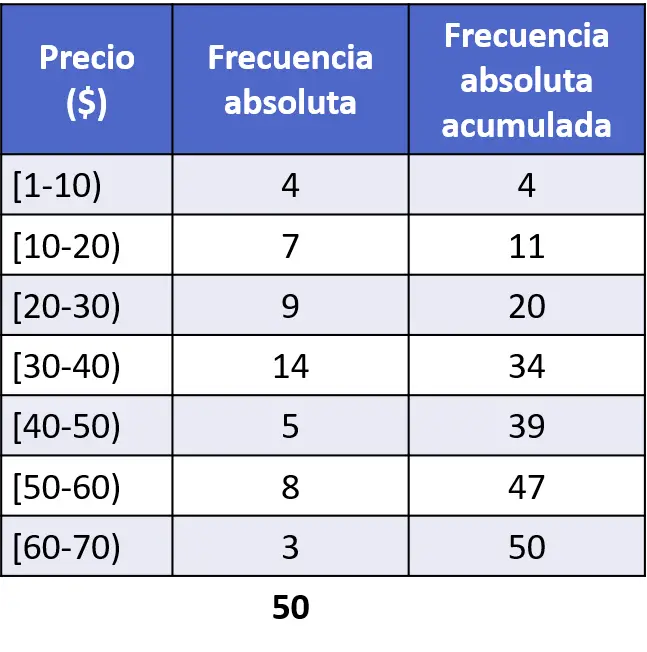
Donc, maintenant que nous avons fait le calcul, nous suivons simplement la même procédure pour tracer un histogramme mais avec les fréquences absolues cumulées :

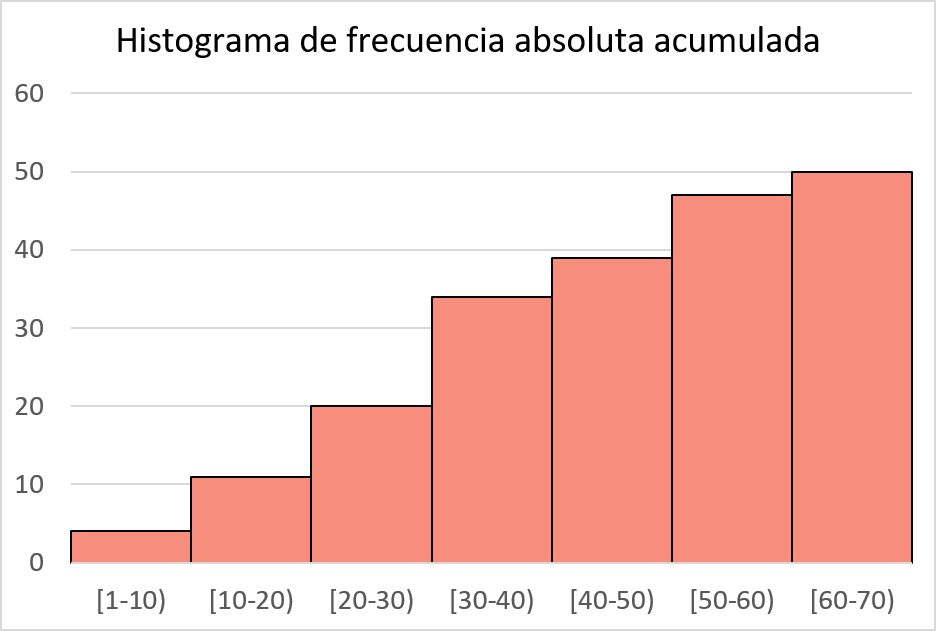
Histogramme des fréquences relatives cumulées

L’histogramme des fréquences relatives cumulées est réalisé de la même manière que les fréquences absolues cumulées, on calcule d’abord les fréquences relatives cumulées de la série de données :

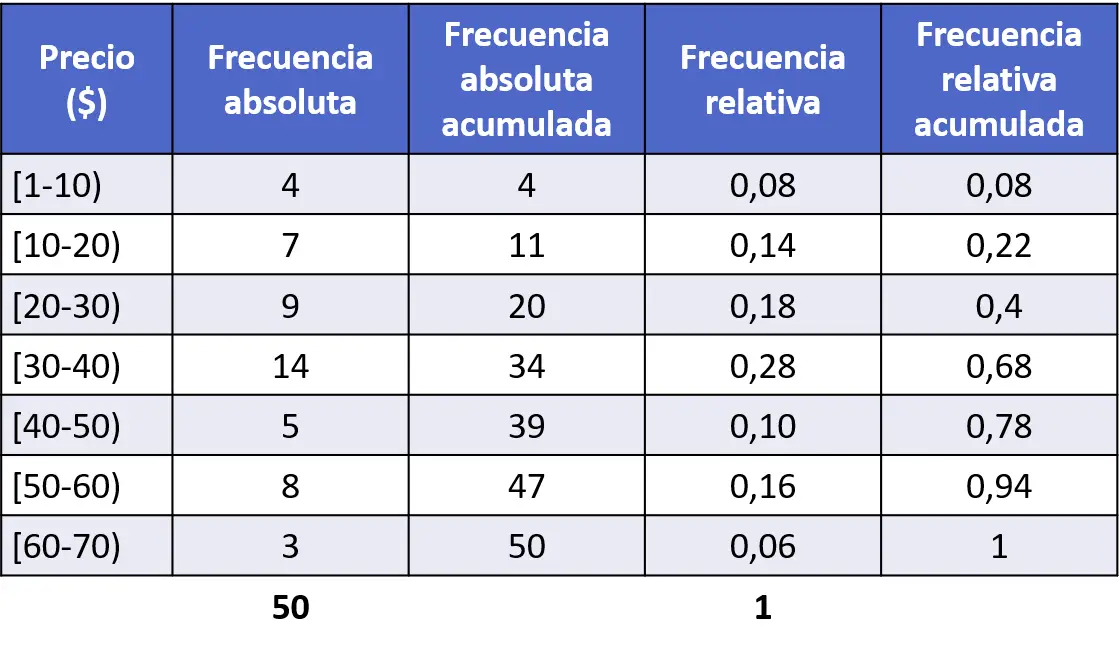
Et puis nous représentons la fréquence relative cumulée dans un histogramme :

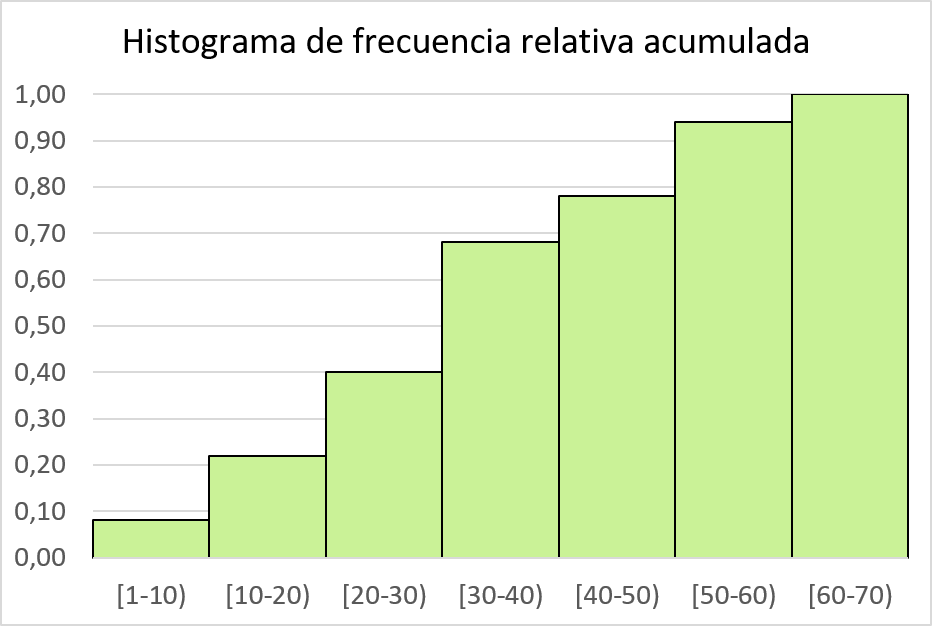
Combinez l’histogramme avec un polygone de fréquence

Parfois, en statistiques, l’histogramme est combiné avec un polygone de fréquence, qui est un ensemble de points reliés par des lignes droites. De cette façon, l’évolution des données est indiquée plus clairement, puisque la ligne du polygone de fréquence permet de mieux visualiser la progression de la série de données.

Pour combiner ces deux types de tracés statistiques, il vous suffit de tracer un point au milieu du haut de chaque barre d’histogramme rectangulaire, puis de joindre les points consécutifs par des lignes droites.

Par exemple, l’histogramme des fréquences absolues réalisé au début de ce post combiné à un polygone de fréquences est :