Histogramme asymétrique à droite : exemples et interprétation

Un histogramme est un type de graphique qui nous permet de visualiser la distribution des valeurs dans un ensemble de données.

On dit qu’un histogramme est asymétrique à droite s’il a une « queue » sur le côté droit de la distribution :

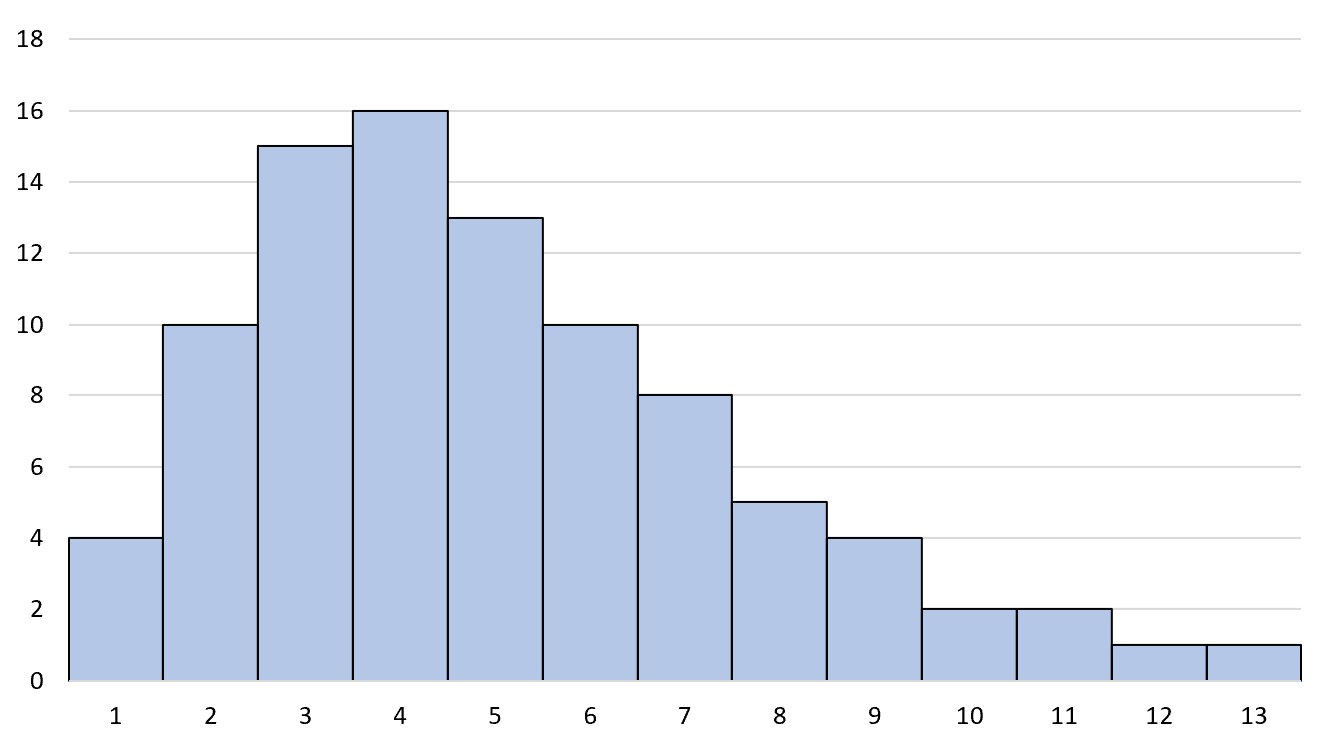
Remarque : Parfois, un histogramme asymétrique à droite est également appelé histogramme asymétrique positivement .

Un histogramme asymétrique à droite possède les deux propriétés suivantes :

1. Le sommet de la distribution se trouve du côté gauche.

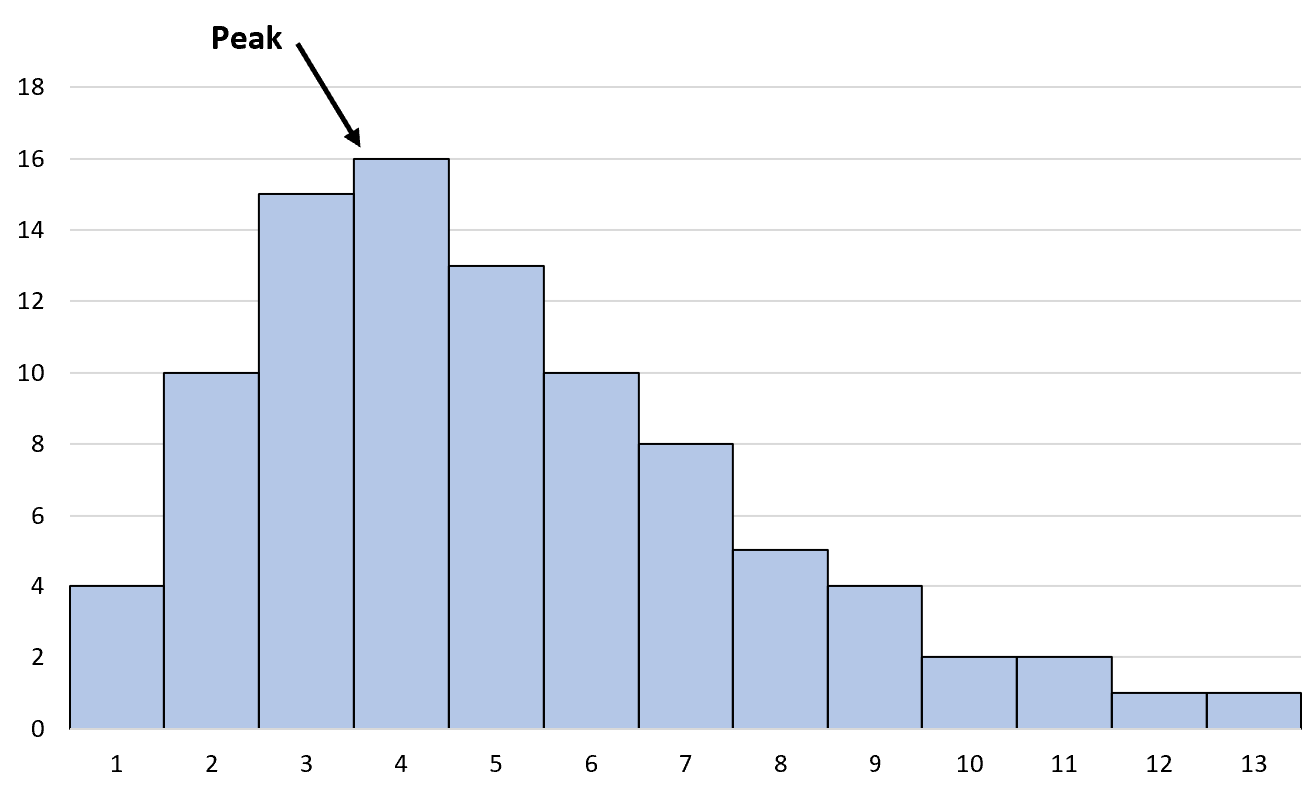
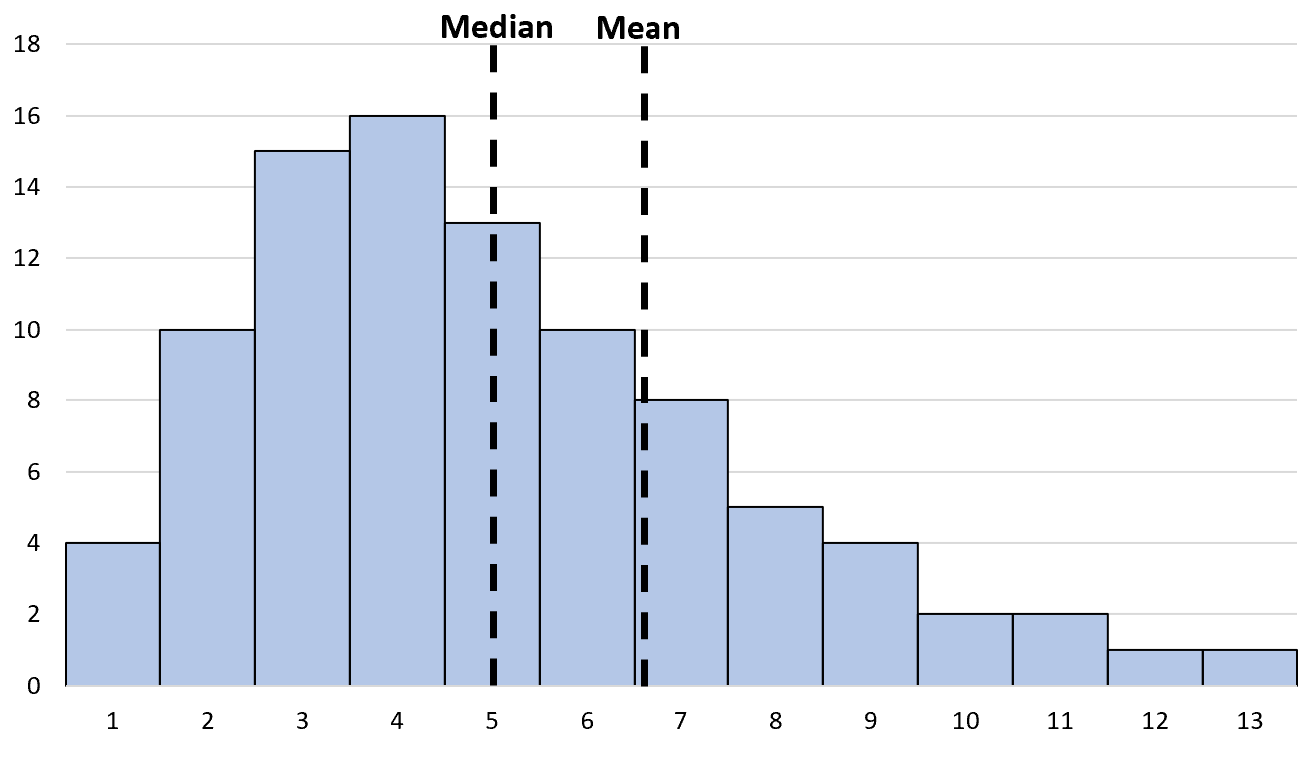
2. La moyenne est supérieure à la médiane.

Qu’est-ce qui fait qu’un histogramme est correctement asymétrique ?

Un histogramme est généralement asymétrique à droite lorsqu’il existe une limite sur la valeur minimale possible mais aucune limite sur la valeur maximale possible.

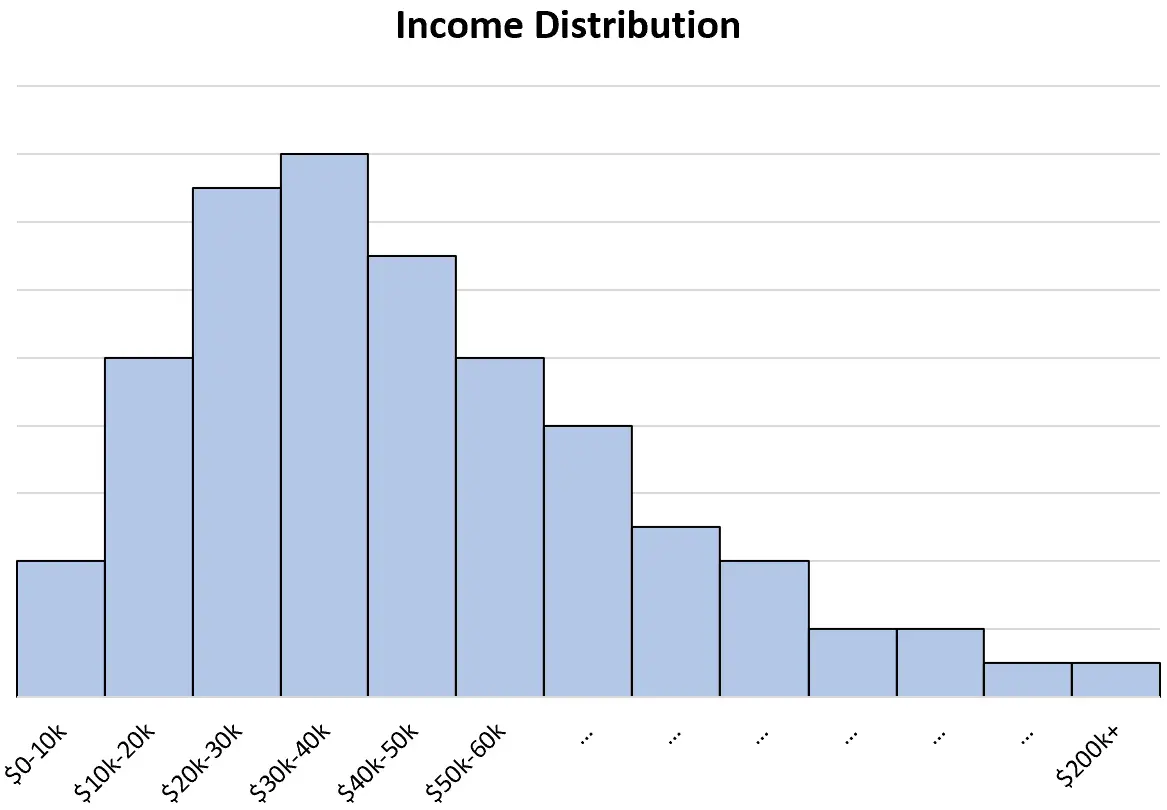
L’exemple réel le plus évident d’un histogramme asymétrique à droite serait la répartition des revenus dans un pays.

Le revenu minimum qu’une personne peut gagner est de zéro dollar, alors qu’il n’y a pas de revenu maximum qu’une personne peut gagner.

En général, la plupart des individus peuvent gagner environ 40 000 dollars par an, mais il existe quelques exceptions qui gagnent plusieurs millions de dollars par an.

Lorsque nous créons un histogramme pour visualiser la répartition des revenus, il sera naturellement asymétrique :

Pourquoi la moyenne est-elle supérieure à la médiane dans un histogramme asymétrique à droite ?

Dans un histogramme asymétrique à droite, la moyenne est supérieure à la médiane car les valeurs élevées sur la « queue » droite de la distribution gonfleront considérablement la valeur de la moyenne.

À titre d’exemple simple, supposons que nous disposions de l’ensemble de données suivant contenant le revenu de 10 personnes :

Ensemble de données 1 : 30 000 $, 35 000 $, 35 000 $, 40 000 $, 50 000 $, 55 000 $, 55 000 $, 70 000 $, 90 000 $, 110 000 $

Voici les valeurs moyennes et médianes de cet ensemble de données :

• Moyenne : 57k$
• Médiane : 52,5k$

Supposons maintenant que nous ayons un autre ensemble de données contenant exactement les mêmes revenus, sauf que la dernière valeur est désormais de 2,5 millions de dollars :

Ensemble de données 2 : 30 000 $, 35 000 $, 35 000 $, 40 000 $, 50 000 $, 55 000 $, 55 000 $, 70 000 $, 90 000 $, 2,5 millions de dollars

Voici les valeurs moyennes et médianes de cet ensemble de données :

• Moyenne : 296k$
• Médiane : 52,5k$

Cette dernière valeur aberrante entraîne une augmentation significative du revenu moyen.

Et si nous traçons cette distribution, ce serait un histogramme asymétrique à droite avec la valeur de 2,5 millions de dollars située sur la « queue » droite de l’histogramme.

La différence entre les histogrammes asymétriques à droite et à gauche

L’opposé d’un histogramme asymétrique à droite est un histogramme asymétrique à gauche .

Il s’agit d’un type d’histogramme qui a une « queue » sur le côté gauche de la distribution :

Ce type d’histogramme a les propriétés suivantes :

1. Le pic de la distribution se trouve du côté droit.

2. La moyenne est inférieure à la médiane.

Notez que ce sont les propriétés exactement opposées d’un histogramme asymétrique à droite.

En savoir plus sur les histogrammes asymétriques à gauche dans ce didacticiel .

Ressources additionnelles

Les didacticiels suivants fournissent des informations supplémentaires sur les histogrammes :

Comment estimer la moyenne et la médiane de n’importe quel histogramme
Comment estimer l’écart type de n’importe quel histogramme
Comment décrire la forme des histogrammes