Comment vérifier les hypothèses de l’ANOVA

Une ANOVA unidirectionnelle est un test statistique utilisé pour déterminer s’il existe ou non une différence significative entre les moyennes de trois groupes indépendants ou plus.

Voici un exemple de cas dans lequel nous pourrions utiliser une ANOVA unidirectionnelle :

Vous divisez au hasard une classe de 90 étudiants en trois groupes de 30. Chaque groupe utilise une technique d’étude différente pendant un mois pour préparer un examen. A la fin du mois, tous les étudiants passent le même examen.

Vous souhaitez savoir si la technique d’étude a ou non un impact sur les résultats aux examens. Vous effectuez donc une ANOVA unidirectionnelle pour déterminer s’il existe une différence statistiquement significative entre les scores moyens des trois groupes.

Avant de pouvoir effectuer une ANOVA unidirectionnelle, nous devons d’abord vérifier que trois hypothèses sont remplies.

1. Normalité – Chaque échantillon a été tiré d’une population normalement distribuée.

2. Variances égales – Les variances des populations dont proviennent les échantillons sont égales.

3. Indépendance – Les observations dans chaque groupe sont indépendantes les unes des autres et les observations au sein des groupes ont été obtenues par un échantillon aléatoire.

Si ces hypothèses ne sont pas remplies, les résultats de notre ANOVA unidirectionnelle pourraient ne pas être fiables.

Dans cet article, nous expliquons comment vérifier ces hypothèses et que faire si l’une d’entre elles n’est pas respectée.

Hypothèse n°1 : normalité

L’ANOVA suppose que chaque échantillon a été tiré d’une population normalement distribuée.

Comment vérifier cette hypothèse dans R :

Pour vérifier cette hypothèse, nous pouvons utiliser deux approches :

• Vérifiez visuellement l’hypothèse à l’aide d’histogrammes ou de tracés QQ .
• Vérifiez l’hypothèse à l’aide de tests statistiques formels comme Shapiro-Wilk, Kolmogorov-Smironov, Jarque-Barre ou D’Agostino-Pearson.

Par exemple, supposons que nous recrutions 90 personnes pour participer à une expérience de perte de poids dans laquelle nous assignons au hasard 30 personnes à suivre soit le programme A, soit le programme B, soit le programme C pendant un mois. Pour voir si le programme a un impact sur la perte de poids, nous souhaitons réaliser une ANOVA unidirectionnelle. Le code suivant illustre comment vérifier l’hypothèse de normalité à l’aide d’histogrammes, de tracés QQ et d’un test de Shapiro-Wilk.

1. Ajuster le modèle ANOVA.

#make this example reproducible
set.seed(0)

#create data frame
data <- data.frame(program = rep(c("A", "B", "C"), each = 30),
                   weight_loss = c(runif(30, 0, 3),
                                   runif(30, 0, 5),
                                   runif(30, 1, 7)))

#fit the one-way ANOVA model
model <- aov(weight_loss ~ program, data = data)

2. Créez un histogramme des valeurs de réponse.

#create histogram
hist(data$weight_loss)

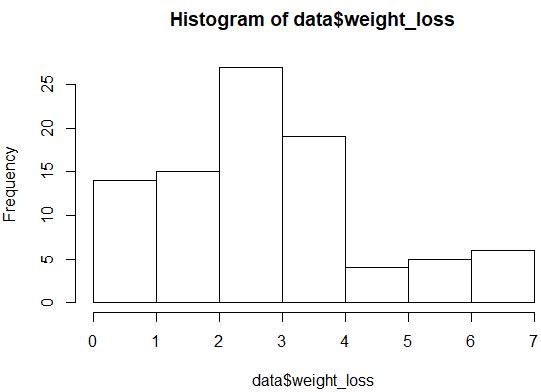
La distribution ne semble pas très normalement distribuée (par exemple, elle n’a pas la forme d’une « cloche »), mais nous pouvons également créer un tracé QQ pour avoir un autre aperçu de la distribution.

3. Créer un tracé QQ des résidus

#create Q-Q plot to compare this dataset to a theoretical normal distribution 
qqnorm(model$residuals)

#add straight diagonal line to plot
qqline(model$residuals)

En général, si les points de données se situent le long d’une ligne diagonale droite dans un tracé QQ, alors l’ensemble de données suit probablement une distribution normale. Dans ce cas, nous pouvons voir qu’il y a un écart notable par rapport à la ligne le long des extrémités, ce qui pourrait indiquer que les données ne sont pas normalement distribuées.

4. Effectuez le test Shapiro-Wilk pour la normalité.

#Conduct Shapiro-Wilk Test for normality 
shapiro.test(data$weight_loss)

#Shapiro-Wilk normality test
#
#data:  data$weight_loss
#W = 0.9587, p-value = 0.005999

Le test de Shapiro-Wilk teste l’hypothèse nulle selon laquelle les échantillons proviennent d’une distribution normale par rapport à l’hypothèse alternative selon laquelle les échantillons ne proviennent pas d’une distribution normale. Dans ce cas, la valeur p du test est de 0,005999 , ce qui est inférieur au niveau alpha de 0,05. Cela suggère que les échantillons ne suivent pas une distribution normale.

Que faire si cette hypothèse n’est pas respectée :

En général, une ANOVA unidirectionnelle est considérée comme assez robuste contre les violations de l’hypothèse de normalité tant que la taille des échantillons est suffisamment grande.

De plus, si vous avez des échantillons extrêmement grands, des tests statistiques comme le test de Shapiro-Wilk vous diront presque toujours que vos données ne sont pas normales. Pour cette raison, il est souvent préférable d’inspecter visuellement vos données à l’aide de graphiques tels que des histogrammes et des tracés QQ. En regardant simplement les graphiques, vous pouvez avoir une assez bonne idée de si les données sont normalement distribuées ou non.

Si l’hypothèse de normalité est gravement violée ou si vous souhaitez simplement être très conservateur, vous avez deux choix :

(1) Transformez les valeurs de réponse de vos données afin que les distributions soient distribuées plus normalement.

(2) Effectuer un test non paramétrique équivalent tel qu’un test de Kruskal-Wallis qui ne nécessite pas l’hypothèse de normalité.

Hypothèse n°2 : variance égale

L’ANOVA suppose que les variances des populations dont proviennent les échantillons sont égales.

Comment vérifier cette hypothèse dans R :

Nous pouvons vérifier cette hypothèse dans R en utilisant deux approches :

• Vérifiez visuellement l’hypothèse à l’aide de boîtes à moustaches.
• Vérifiez l’hypothèse à l’aide de tests statistiques formels comme le test de Bartlett.

Le code suivant illustre comment procéder, en utilisant le même faux ensemble de données de perte de poids que nous avons créé précédemment.

1. Créez des boîtes à moustaches.

#Create box plots that show distribution of weight loss for each group
boxplot(weight_loss ~ program, xlab='Program', ylab='Weight Loss', data=data)

La variance de la perte de poids dans chaque groupe peut être observée par la longueur de chaque boîte à moustaches. Plus la boîte est longue, plus la variance est élevée. Par exemple, nous pouvons voir que la variance est un peu plus élevée pour les participants au programme C par rapport au programme A et au programme B.

2. Effectuez le test de Bartlett.

#Create box plots that show distribution of weight loss for each group
bartlett.test(weight_loss ~ program, data=data)

#Bartlett test of homogeneity of variances
#
#data:  weight_loss by program
#Bartlett's K-squared = 8.2713, df = 2, p-value = 0.01599

Le test de Bartlett teste l’hypothèse nulle selon laquelle les échantillons ont des variances égales par rapport à l’hypothèse alternative selon laquelle les échantillons n’ont pas des variances égales. Dans ce cas, la valeur p du test est de 0,01599 , ce qui est inférieur au niveau alpha de 0,05. Cela suggère que les échantillons n’ont pas tous la même variance.

Que faire si cette hypothèse n’est pas respectée :

En général, une ANOVA unidirectionnelle est considérée comme assez robuste aux violations de l’hypothèse des variances égales tant que chaque groupe a la même taille d’échantillon.

Cependant, si les tailles d’échantillon ne sont pas les mêmes et que cette hypothèse est gravement violée, vous pouvez à la place exécuter un test de Kruskal-Wallis , qui est la version non paramétrique de l’ANOVA unidirectionnelle.

Hypothèse n°3 : Indépendance

L’ANOVA suppose :

• Les observations de chaque groupe sont indépendantes des observations de tous les autres groupes.
• Les observations au sein de chaque groupe ont été obtenues par un échantillon aléatoire.

Comment vérifier cette hypothèse :

Il n’existe aucun test formel que vous pouvez utiliser pour vérifier que les observations dans chaque groupe sont indépendantes et qu’elles ont été obtenues par un échantillon aléatoire. La seule façon de satisfaire à cette hypothèse est d’utiliser un plan randomisé.

Que faire si cette hypothèse n’est pas respectée :

Malheureusement, vous ne pouvez pas faire grand-chose si cette hypothèse n’est pas respectée. En termes simples, si les données ont été collectées de manière à ce que les observations dans chaque groupe ne soient pas indépendantes des observations dans d’autres groupes, ou si les observations au sein de chaque groupe n’ont pas été obtenues par un processus randomisé, les résultats de l’ANOVA ne seront pas fiables.

Si cette hypothèse n’est pas respectée, la meilleure chose à faire est de reconstituer l’expérience en utilisant un plan randomisé.

Lectures complémentaires :

Comment effectuer une ANOVA unidirectionnelle dans R
Comment effectuer une ANOVA unidirectionnelle dans Excel