Les cinq hypothèses de la corrélation de Pearson

Le coefficient de corrélation de Pearson (également connu sous le nom de « coefficient de corrélation produit-moment ») mesure l’association linéaire entre deux variables.

Il prend toujours une valeur comprise entre -1 et 1 où :

• -1 indique une corrélation linéaire parfaitement négative entre deux variables
• 0 indique aucune corrélation linéaire entre deux variables
• 1 indique une corrélation linéaire parfaitement positive entre deux variables

Cependant, avant de calculer le coefficient de corrélation de Pearson entre deux variables, nous devons nous assurer que cinq hypothèses sont remplies :

1. Niveau de mesure : Les deux variables doivent être mesurées au niveau de l’ intervalle ou du rapport .

2. Relation linéaire : Il doit exister une relation linéaire entre les deux variables.

3. Normalité : les deux variables doivent avoir une distribution à peu près normale.

4. Paires associées : chaque observation de l’ensemble de données doit avoir une paire de valeurs.

5. Aucune valeur aberrante : il ne doit y avoir aucune valeur aberrante extrême dans l’ensemble de données.

Dans cet article, nous fournissons une explication de chaque hypothèse ainsi que la manière de déterminer si l’hypothèse est remplie.

Hypothèse 1 : Niveau de mesure

Pour calculer un coefficient de corrélation de Pearson entre deux variables, les deux variables doivent être mesurées au niveau de l’ intervalle ou du rapport .

Le graphique suivant fournit une explication rapide des quatre niveaux auxquels les variables peuvent être mesurées :

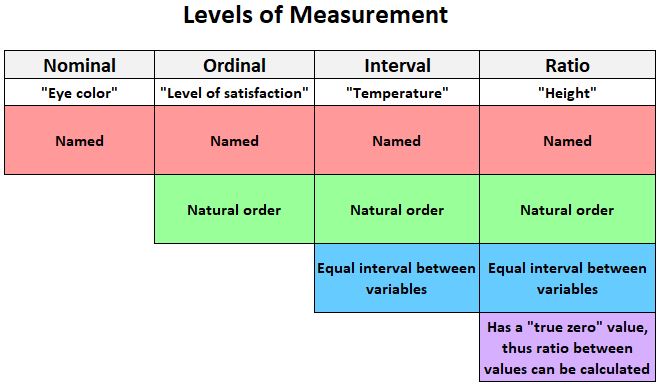
Voici quelques exemples de variables qui peuvent être mesurées sur une échelle d’intervalle :

• Température : Mesurée en Fahrenheit ou Celsius
• Cotes de crédit : mesurées de 300 à 850
• Scores SAT : mesurés de 400 à 1 600

Voici quelques exemples de variables qui peuvent être mesurées sur une échelle de ratio :

• Hauteur : Mesurée en centimètres, pouces, pieds, etc.
• Poids : mesuré en kilogrammes, en livres, etc.
• Longueur : Mesurée en centimètres, pouces, pieds, etc.

Si les variables sont mesurées à un niveau ordinal , vous devez alors calculer le coefficient de corrélation de Spearman entre elles.

Connexes :  Niveaux de mesure : nominal, ordinal, intervalle et rapport

Hypothèse 2 : Relation linéaire

Pour calculer un coefficient de corrélation de Pearson entre deux variables, il doit exister une relation linéaire entre les deux variables.

Le moyen le plus simple de vérifier cette hypothèse consiste simplement à créer un nuage de points des deux variables. Si les points du tracé suivent à peu près une ligne droite, alors une relation linéaire existe :

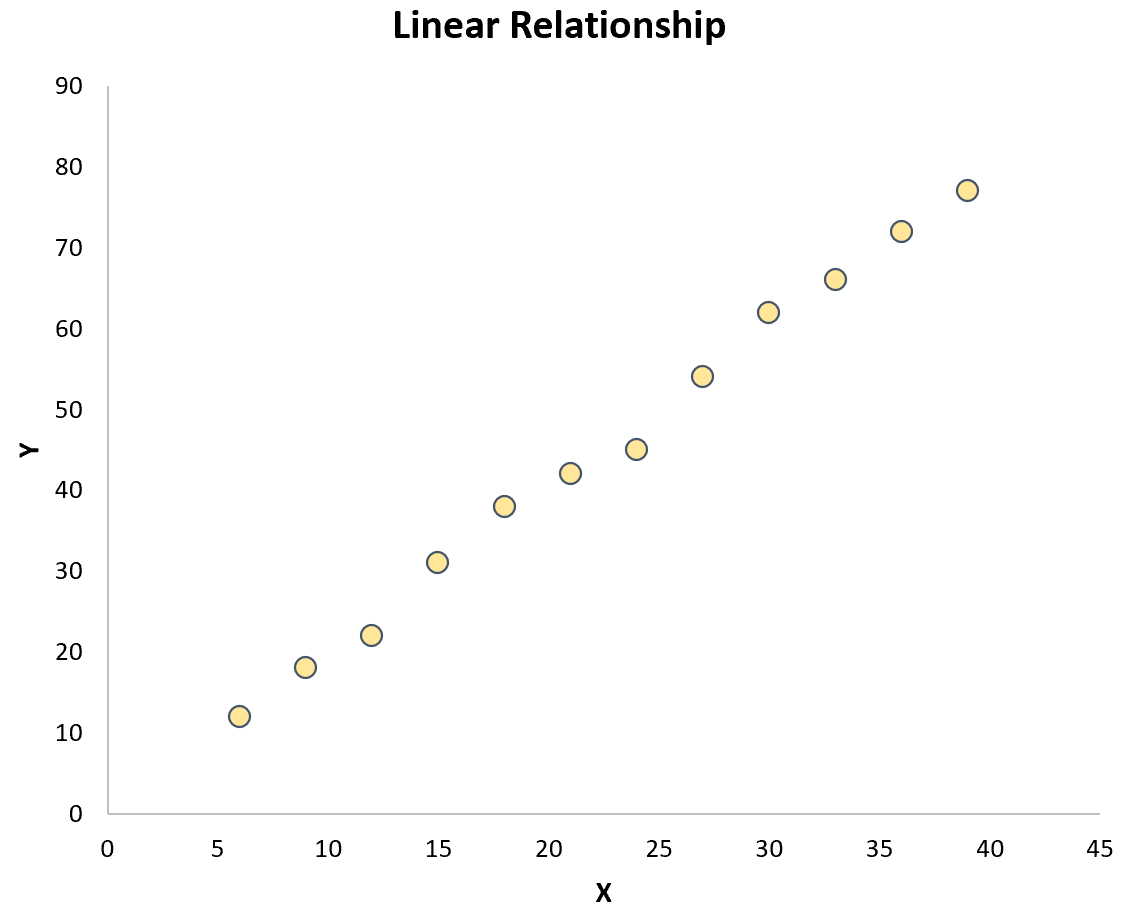
Cependant, si les points sont dispersés de manière aléatoire sur le tracé ou s’ils présentent un autre type de relation (comme quadratique), alors une relation linéaire n’existe pas entre les variables :

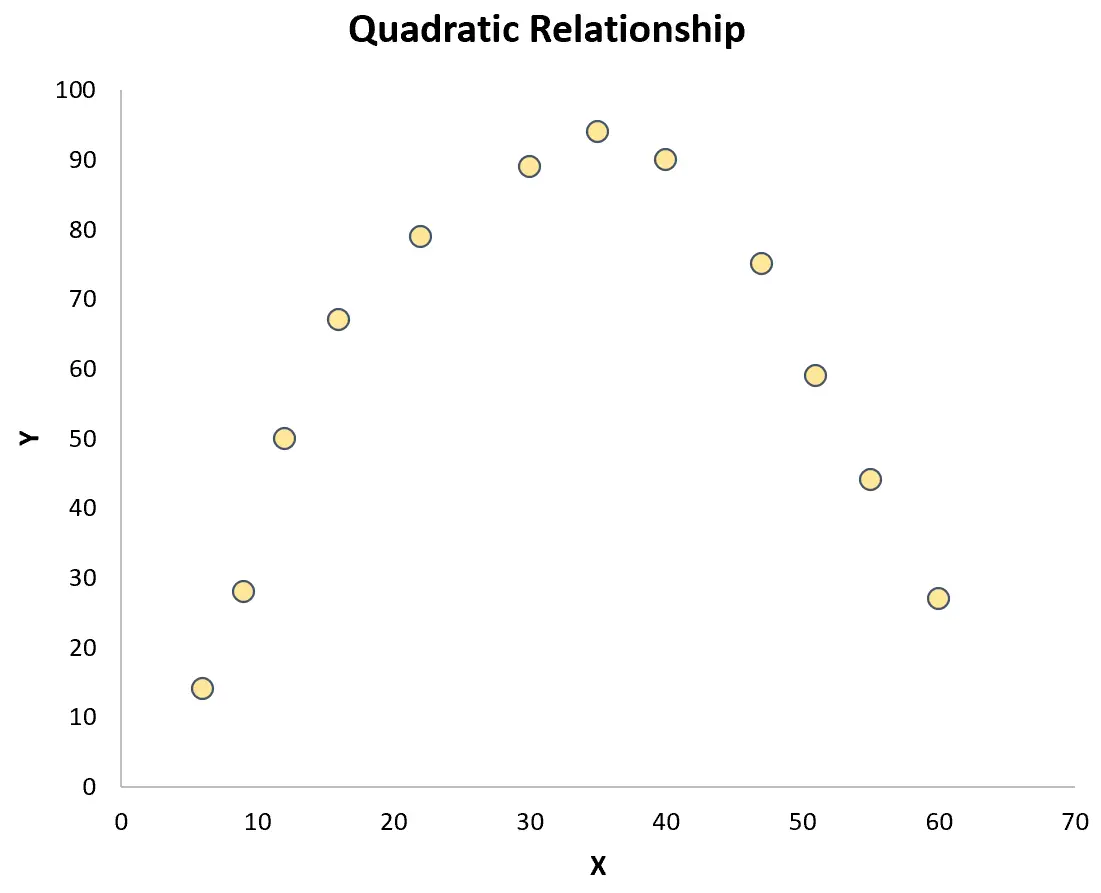
Dans ce cas, un coefficient de corrélation de Pearson ne permettra pas de bien capturer la relation entre les variables.

Hypothèse 3 : normalité

Un coefficient de corrélation de Pearson suppose également que les deux variables sont distribuées à peu près normalement .

Vous pouvez vérifier cette hypothèse visuellement en créant un histogramme ou un tracé QQ pour chaque variable.

1. Histogramme

Si l’histogramme d’un ensemble de données est à peu près en forme de cloche, il est probable que les données soient distribuées normalement.

2. Terrain QQ

Un tracé QQ, abréviation de « quantile-quantile », est un type de tracé qui affiche les quantiles théoriques le long de l’axe des x (c’est-à-dire où se trouveraient vos données si elles suivaient une distribution normale) et des quantiles d’échantillons le long de l’axe des y. (c’est-à-dire où se trouvent réellement vos données).

Si les valeurs des données suivent une ligne à peu près droite formant un angle de 45 degrés, alors les données sont supposées être distribuées normalement.

Vous pouvez également effectuer un test statistique formel pour déterminer si une variable est normalement distribuée.

Si la valeur p du test est inférieure à un certain niveau de signification (comme α = 0,05), vous disposez alors de preuves suffisantes pour affirmer que les données ne sont pas normalement distribuées.

Il existe trois tests statistiques couramment utilisés pour tester la normalité :

1. Le test Jarque-Bera

• Comment effectuer un test Jarque-Bera dans Excel
• Comment effectuer un test Jarque-Bera dans R
• Comment effectuer un test Jarque-Bera en Python

2. Le test de Shapiro-Wilk

• Comment effectuer un test Shapiro-Wilk dans R
• Comment effectuer un test Shapiro-Wilk en Python

3. Le test de Kolmogorov-Smirnov

• Comment effectuer un test de Kolmogorov-Smirnov dans R
• Comment effectuer un test Kolmogorov-Smirnov en Python

Hypothèse 4 : Paires apparentées

Un coefficient de corrélation de Pearson suppose également que chaque observation de l’ensemble de données doit avoir une paire de valeurs.

Cette hypothèse est facile à vérifier. Par exemple, si vous calculez la corrélation entre le poids et la taille, vérifiez simplement que chaque observation de l’ensemble de données comporte une mesure pour le poids et une mesure pour la taille.

Hypothèse 5 : aucune valeur aberrante

Un coefficient de corrélation de Pearson suppose également qu’il n’y a pas de valeurs aberrantes extrêmes dans l’ensemble de données, car les valeurs aberrantes affectent fortement le calcul du coefficient de corrélation.

Pour illustrer cela, considérons l’ensemble de données suivant :

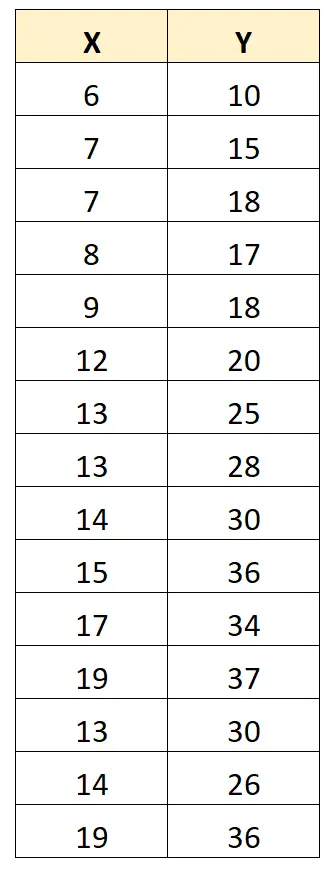
Le coefficient de corrélation de Pearson entre X et Y est de 0,949 .

Cependant, supposons que nous ayons une valeur aberrante dans l’ensemble de données :

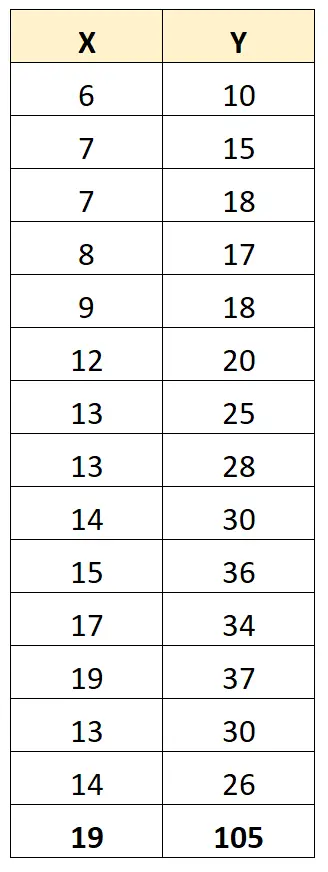
Le coefficient de corrélation de Pearson entre X et Y est désormais de 0,711 .

Une valeur aberrante modifie considérablement le coefficient de corrélation de Pearson entre les deux variables. Dans ce cas, il pourrait être judicieux de supprimer la valeur aberrante de l’ensemble de données.

Connexe : Le guide complet : Quand supprimer les valeurs aberrantes dans les données

Ressources additionnelles

Les didacticiels suivants fournissent des informations supplémentaires sur la corrélation de Pearson :

Introduction au coefficient de corrélation de Pearson
Comment rapporter la corrélation de Pearson au format APA
Comment calculer manuellement un coefficient de corrélation de Pearson