Les trois hypothèses formulées dans un test t apparié

Un test t pour échantillons appariés est utilisé pour comparer les moyennes de deux échantillons lorsque chaque observation dans un échantillon peut être associée à une observation dans l’autre échantillon.

Ce type de test fait les hypothèses suivantes sur les données :

1. Indépendance : chaque observation doit être indépendante de toute autre observation.

2. Normalité : Les différences entre les paires doivent être à peu près normalement distribuées.

3. Pas de valeurs aberrantes extrêmes : Il ne devrait y avoir aucune valeur aberrante extrême dans les différences.

Si une ou plusieurs de ces hypothèses ne sont pas respectées, les résultats du test t pour échantillons appariés peuvent être peu fiables ou trompeurs.

Dans ce didacticiel, nous fournissons une explication de chaque hypothèse, comment déterminer si l’hypothèse est satisfaite et que faire si elle n’est pas respectée.

Hypothèse 1 : Indépendance

Un test t pour échantillons appariés suppose que chaque observation est indépendante de toutes les autres observations.

Comment vérifier cette hypothèse

Le moyen le plus simple de vérifier cette hypothèse est de vérifier que chaque observation a été collectée à l’aide d’une méthode d’échantillonnage aléatoire .

Si une méthode d’échantillonnage aléatoire a été utilisée (telle qu’un échantillonnage aléatoire simple), nous pouvons alors supposer que chaque observation est indépendante de toutes les autres observations.

Que faire si cette hypothèse n’est pas respectée

Si cette hypothèse n’est pas respectée, les résultats du test t pour échantillons appariés sont complètement invalides.

Dans ce scénario, il est préférable de collecter de nouvelles observations à l’aide d’une méthode d’échantillonnage aléatoire pour garantir que chaque observation est indépendante.

Hypothèse 2 : normalité

Un test t pour échantillons appariés suppose que les différences entre les paires doivent être à peu près normalement distribuées.

Il s’agit d’une hypothèse cruciale car si les différences entre les paires ne sont pas distribuées normalement, il n’est pas valable d’utiliser la valeur p du test pour tirer des conclusions.

Comment vérifier cette hypothèse

Le moyen le plus simple de vérifier cette hypothèse consiste simplement à créer un histogramme des différences appariées et à vérifier visuellement si l’histogramme présente ou non une forme de cloche.

Par exemple, si l’histogramme ressemble à ceci, nous dirions que l’hypothèse de normalité est remplie :

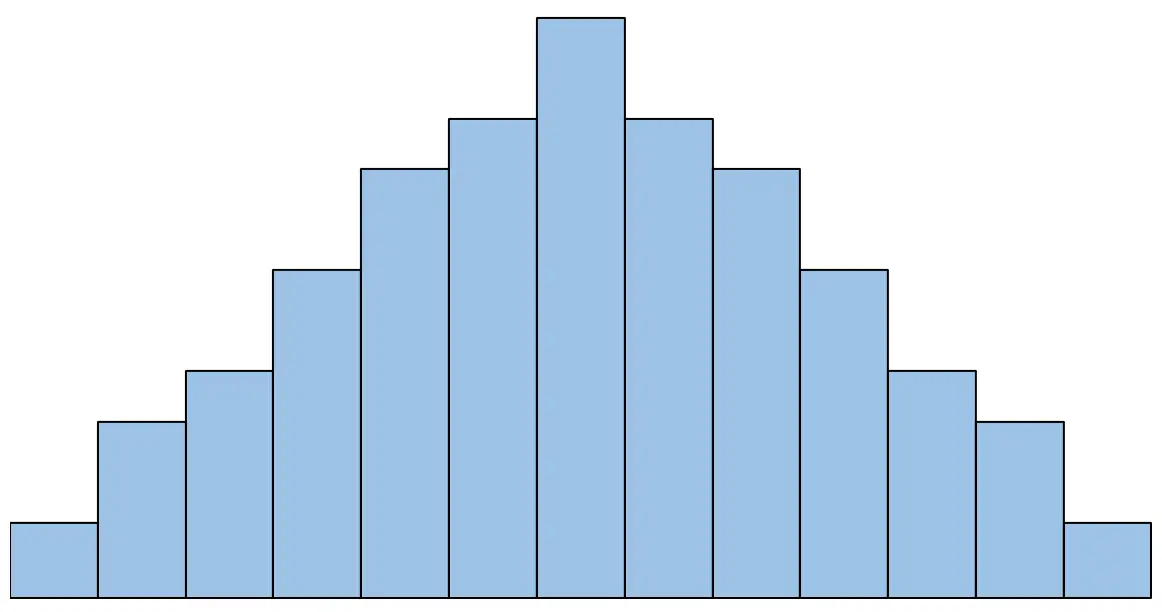
Cependant, si l’histogramme ressemble à ceci, nous dirions que l’hypothèse de normalité n’est pas remplie :

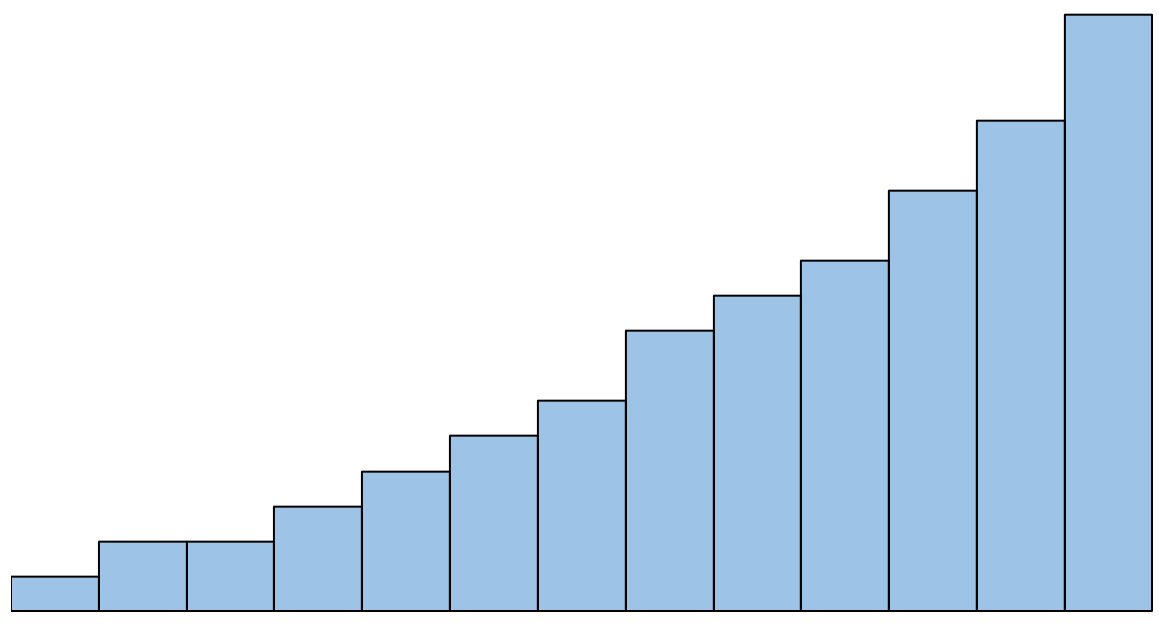
Que faire si cette hypothèse n’est pas respectée

Si cette hypothèse n’est pas respectée, nous pouvons effectuer un test de rang signé de Wilcoxon , qui est considéré comme l’équivalent non paramétrique du test t pour échantillons appariés et ne suppose pas que les différences appariées sont normalement distribuées.

Hypothèse 3 : pas de valeurs aberrantes extrêmes

Un test t pour échantillons appariés suppose qu’il n’y a pas de valeurs aberrantes extrêmes dans les données.

Comment vérifier cette hypothèse

Le moyen le plus simple de vérifier cette hypothèse est de créer un diagramme en boîte des différences appariées et de vérifier visuellement s’il existe des valeurs aberrantes.

Par exemple, supposons que le diagramme en boîte des différences appariées ressemble à ceci :

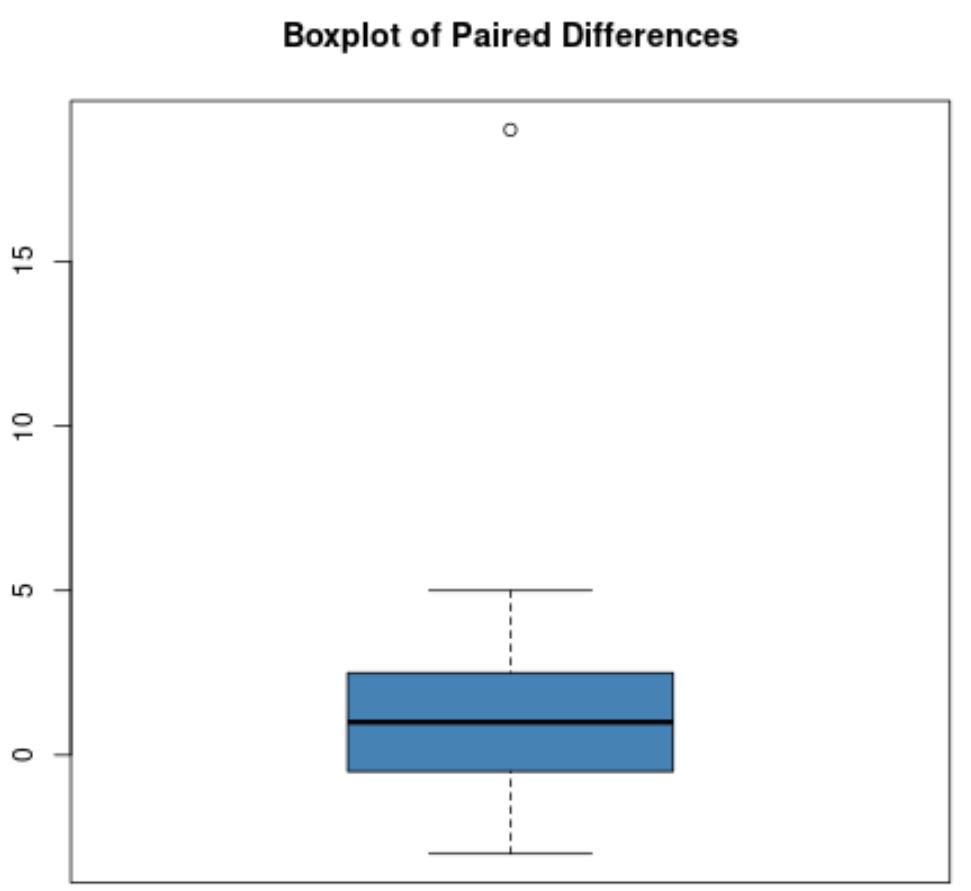
La plupart des différences appariées sont proches de zéro, mais il existe une différence appariée égale à environ 19, ce qui constitue clairement une valeur aberrante.

Remarque : Un cercle est généralement utilisé dans une boîte à moustaches pour indiquer une valeur aberrante.

Cependant, supposons que le diagramme en boîte des différences appariées ressemble à ceci :

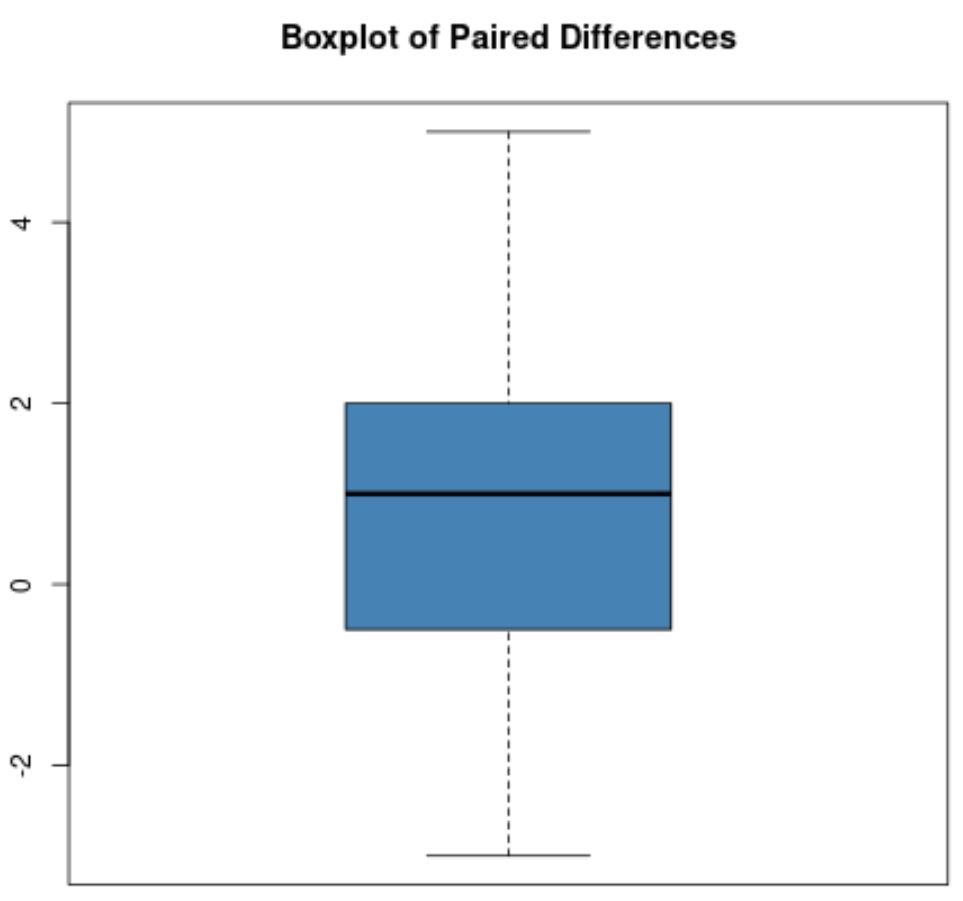
Il n’y a pas de valeurs aberrantes claires dans ce boxplot, nous supposerons donc qu’il n’y a pas de valeurs aberrantes extrêmes dans les données.

Que faire si cette hypothèse n’est pas respectée

Si cette hypothèse n’est pas respectée, les résultats du test t pour échantillons appariés pourraient être anormalement affectés par la valeur aberrante.

Dans ce scénario, vous pouvez supprimer la valeur aberrante si vous pensez qu’elle représente un point de données défectueux ou qu’elle est le résultat d’une erreur de saisie de données.

Alternativement, vous pouvez conserver la valeur aberrante et simplement la noter lorsque vous rapportez les résultats du test t pour échantillons appariés.

Ressources additionnelles

Les didacticiels suivants expliquent les hypothèses formulées dans d’autres tests statistiques :

Les quatre hypothèses formulées dans un test t
Les quatre hypothèses d’un test du chi carré
Les quatre hypothèses des tests paramétriques