Le guide complet : Comment vérifier les hypothèses MANOVA

Une MANOVA (analyse multivariée de la variance) est utilisée pour analyser comment une ou plusieurs variables factorielles affectent plusieurs variables de réponse.

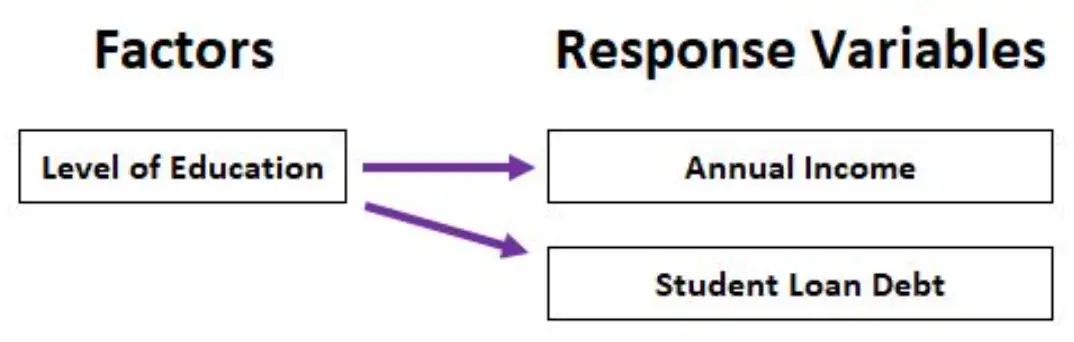
Par exemple, nous pourrions utiliser une MANOVA pour analyser comment le niveau d’éducation (diplôme d’études secondaires, diplôme d’associé, baccalauréat, maîtrise) affecte à la fois le revenu annuel et la dette totale des prêts étudiants.

Connexes : Les différences entre ANOVA, ANCOVA, MANOVA et MANCOVA

Chaque fois que nous effectuons une MANOVA, nous devons vérifier que les hypothèses suivantes sont respectées :

1. Normalité multivariée – Les variables de réponse sont multivariées normalement distribuées au sein de chaque groupe de variable(s) factorielle(s).

2. Indépendance – Chaque observation est échantillonnée de manière aléatoire et indépendante dans la population.

3. Variance égale – Les matrices de covariance de population de chaque groupe sont égales.

4. Pas de valeurs aberrantes multivariées – Il n’y a pas de valeurs aberrantes multivariées extrêmes.

Dans cet article, nous fournissons une explication de chaque hypothèse ainsi que la manière de déterminer si l’hypothèse est remplie.

Hypothèse 1 : Normalité multivariée

Une MANOVA suppose que les variables de réponse sont multivariées normalement distribuées au sein de chaque groupe de la variable factorielle.

S’il y a au moins 20 observations pour chaque combinaison facteur * variable de réponse, alors nous pouvons supposer que l’hypothèse de normalité multivariée est remplie.

S’il y a moins de 20 observations pour chaque combinaison facteur * variable de réponse, nous pouvons créer une matrice de nuages de points pour visualiser les résidus et vérifier visuellement si cette hypothèse est remplie.

Heureusement, il est bien connu que MANOVA est robuste aux écarts par rapport à la normalité multivariée, de sorte que des écarts faibles à modérés ne posent généralement aucun problème.

Hypothèse 2 : Indépendance

Une MANOVA suppose que chaque observation est échantillonnée de manière aléatoire et indépendante dans la population.

Tant qu’une méthode d’échantillonnage probabiliste (chaque membre d’une population a une probabilité égale d’être sélectionné pour faire partie de l’échantillon) est utilisée pour collecter les données, nous pouvons supposer que chaque observation a été échantillonnée de manière aléatoire et indépendante.

Voici des exemples de méthodes d’échantillonnage probabiliste :

• Échantillonnage aléatoire simple
• Échantillonnage aléatoire stratifié
• Échantillonnage aléatoire en grappes
• Échantillonnage aléatoire systématique

Hypothèse 3 : variance égale

Une MANOVA suppose que les matrices de covariance de population de chaque groupe sont égales.

La manière la plus courante de vérifier cette hypothèse consiste à utiliser le test M de Box. Ce test est connu pour être assez strict, c’est pourquoi nous utilisons généralement un niveau de signification de 0,001 pour déterminer si les matrices de covariance de la population sont égales ou non.

Si la valeur p du test M de Box est supérieure à 0,001, nous pouvons supposer que cette hypothèse est remplie.

Heureusement, même si la valeur p du test est inférieure à 0,001, une MANOVA a tendance à être robuste face aux écarts par rapport à cette hypothèse.

Pour que les matrices de covariance non égales posent problème, les différences entre les matrices de covariance doivent être assez extrêmes.

Hypothèse 4 : pas de valeurs aberrantes multivariées

Une MANOVA suppose qu’il n’y a pas de valeurs aberrantes multivariées extrêmes présentes dans les données qui pourraient influencer de manière significative les résultats.

La manière la plus courante de vérifier cette hypothèse consiste à calculer la distance de Mahalanobis pour chaque observation, qui représente la distance entre deux points dans un espace multivarié.

Si la valeur p correspondante pour une distance de Mahalanobis d’une observation est inférieure à 0,001, nous déclarons généralement que cette observation est une valeur aberrante extrême.

Reportez-vous aux didacticiels suivants pour voir comment calculer la distance de Mahalanobis dans divers logiciels statistiques :

• Comment calculer la distance de Mahalanobis en R
• Comment calculer la distance de Mahalanobis dans SPSS
• Comment calculer la distance de Mahalanobis en Python

Ressources additionnelles

Les tutoriels suivants expliquent comment réaliser une MANOVA dans divers logiciels statistiques :

Comment effectuer une MANOVA dans R
Comment effectuer une MANOVA dans SPSS
Comment effectuer une MANOVA dans Stata