Inférence et prédiction : quelle est la différence ?

Souvent, dans le domaine des statistiques, nous souhaitons utiliser des données pour l’une des deux raisons suivantes :

(1) Inférence : nous voulons comprendre la nature de la relation entre les variables prédictives et la variable de réponse dans un ensemble de données existant.

(2) Prédiction : nous souhaitons utiliser un ensemble de données existant pour construire un modèle qui prédit la valeur de la variable de réponse d’une nouvelle observation.

Par exemple, supposons que nous disposions de l’ensemble de données suivant contenant des informations sur les maisons :

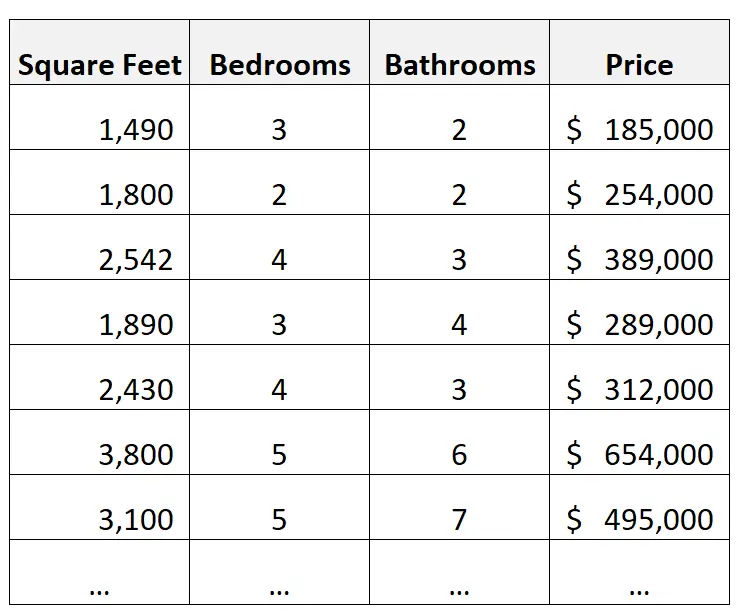
Un exemple d’inférence :

Supposons que nous construisions un modèle de régression linéaire multiple utilisant les pieds carrés, le nombre de chambres et le nombre de salles de bains comme variables prédictives et le prix comme variable de réponse.

Nous pourrions alors utiliser les coefficients de régression pour comprendre la variation moyenne du prix associée à une variation d’une unité dans chacune des variables prédictives.

Par exemple, nous pourrions comprendre dans quelle mesure le prix change (en moyenne) avec chaque chambre supplémentaire, chaque salle de bain supplémentaire et chaque pied carré supplémentaire.

Un exemple de prédiction :

Nous pourrions construire le même modèle de régression linéaire multiple et l’utiliser pour prédire la valeur d’une nouvelle maison en fonction de sa superficie en pieds carrés, du nombre de chambres et du nombre de salles de bains.

Par exemple, nous pourrions utiliser le modèle pour prédire le prix d’une maison neuve comprenant 3 chambres, 3 salles de bains et 2 000 pieds carrés.

Nous pourrions alors comparer notre prévision avec le prix d’inscription réel et évaluer si la maison semble ou non sous-évaluée ou surévaluée.

Les exemples suivants illustrent la différence entre l’inférence et la prédiction dans différents scénarios :

Exemple 1 : Inférence et prédiction dans le sport

Supposons que nous disposions de l’ensemble de données suivant contenant des informations sur les équipes professionnelles de basket-ball :

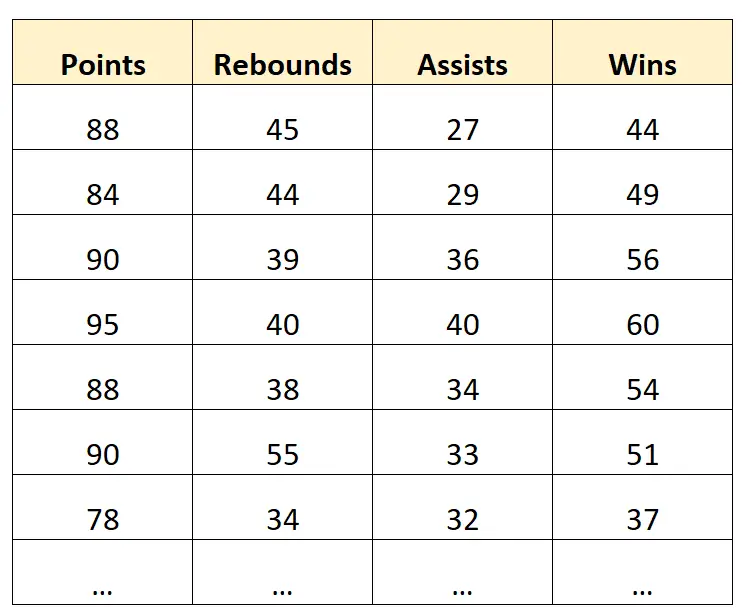
Un exemple d’inférence :

Supposons que nous construisions un modèle de régression linéaire multiple utilisant les points, les rebonds et les assistances comme variables prédictives et les victoires comme variable de réponse.

Nous pourrions ensuite utiliser le modèle pour comprendre dans quelle mesure le nombre de victoires change (en moyenne) avec chaque point, rebond et passe décisive supplémentaires.

Un exemple de prédiction :

Nous pourrions construire le même modèle de régression linéaire multiple et l’utiliser pour prédire le nombre de victoires qu’une équipe obtiendra en fonction de son nombre de points, de rebonds et de passes décisives.

Par exemple, nous pourrions utiliser le modèle pour prédire le nombre de victoires qu’obtiendra une équipe avec 90 points, 40 rebonds et 30 passes décisives.

Exemple 2 : Inférence et prédiction en entreprise

Supposons que nous disposions de l’ensemble de données suivant contenant des informations sur les revenus annuels (en millions) de diverses entreprises :

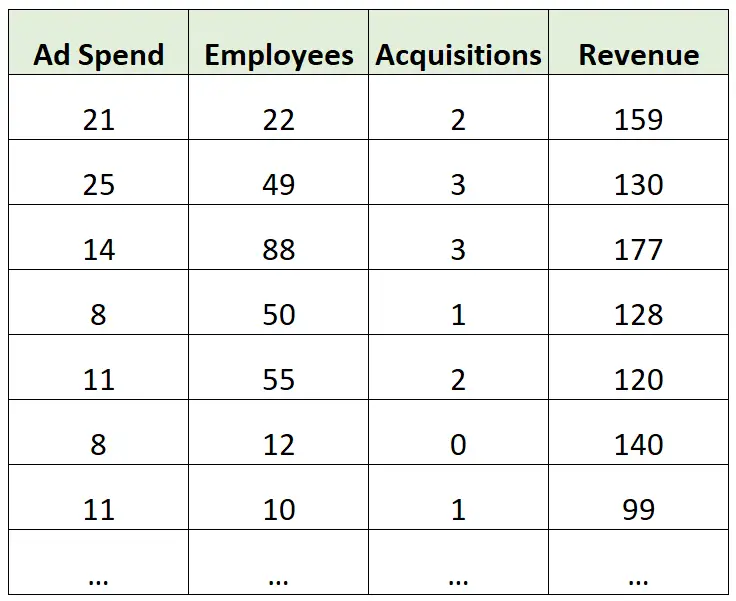
Un exemple d’inférence :

Supposons que nous construisions un modèle de régression linéaire multiple utilisant les dépenses publicitaires, le nombre d’employés et le total des acquisitions comme variables prédictives et le revenu annuel comme variable de réponse.

Nous pourrions ensuite utiliser le modèle pour comprendre dans quelle mesure le chiffre d’affaires annuel total change (en moyenne) avec chaque dollar supplémentaire dépensé en publicité, chaque employé supplémentaire et chaque acquisition supplémentaire.

Un exemple de prédiction :

Nous pourrions construire le même modèle de régression linéaire multiple et l’utiliser pour prédire le chiffre d’affaires annuel d’une entreprise en fonction de ses dépenses marketing totales, du nombre d’employés et du total des acquisitions.

Par exemple, nous pourrions utiliser le modèle pour prédire le chiffre d’affaires annuel d’une entreprise qui dépense 25 millions de dollars en publicité, compte 40 employés et a réalisé 2 acquisitions.

Ressources additionnelles

Les didacticiels suivants offrent des informations supplémentaires sur les termes importants à comprendre dans les statistiques :

Statistiques descriptives ou inférentielles : quelle est la différence ?
Niveaux de mesure : nominal, ordinal, intervalle et rapport
Variables qualitatives et quantitatives : quelle est la différence ?