Interpolation ou extrapolation : quelle est la différence ?

Deux termes que les étudiants confondent souvent en statistique sont interpolation et extrapolation .

Voici la différence :

L’interpolation fait référence à la prédiction de valeurs situées à l’intérieur d’une plage de points de données.

L’extrapolation fait référence à la prédiction de valeurs qui se situent en dehors d’une plage de points de données.

L’exemple suivant illustre la différence entre les deux termes.

Exemple : interpolation et extrapolation

Supposons que nous ayons l’ensemble de données suivant :

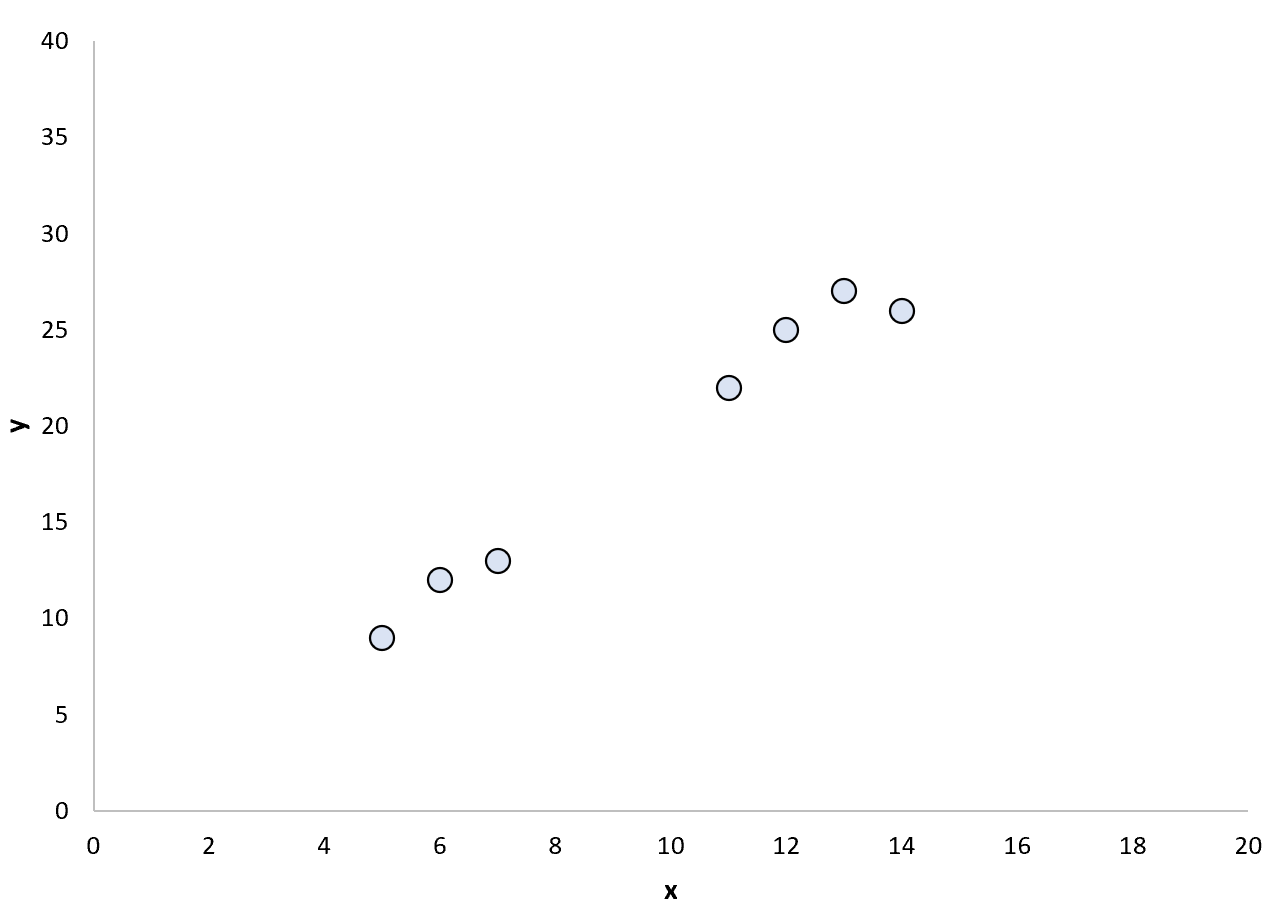
Nous pouvons décider d’adapter un modèle de régression linéaire simple à ces points :

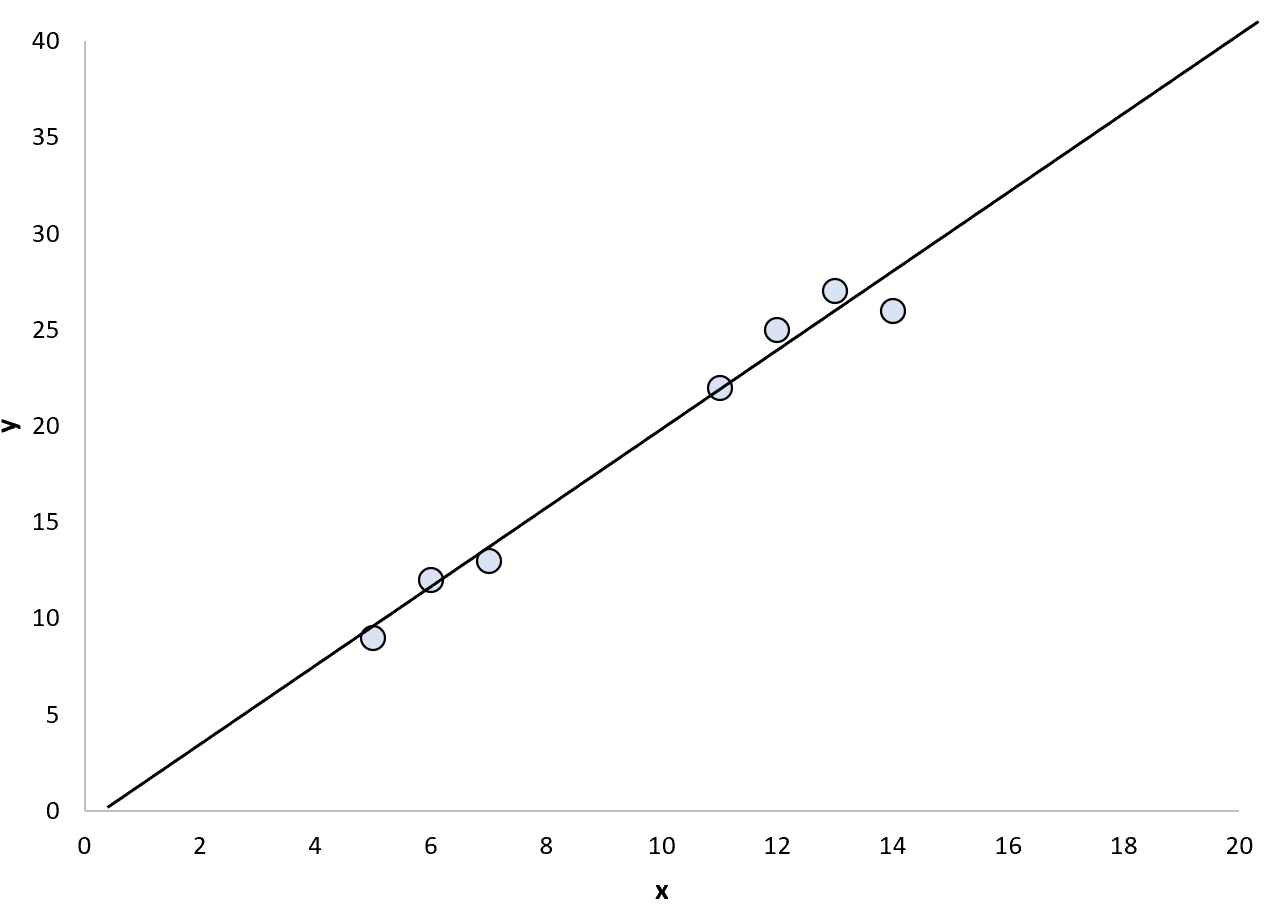
Nous pourrions ensuite utiliser le modèle de régression ajusté pour prédire les valeurs des points à la fois à l’intérieur et à l’extérieur de la plage de points de données.

Lorsque nous utilisons le modèle de régression ajusté pour prédire les valeurs de points à l’intérieur de la plage existante de points de données, on parle d’ interpolation.

À l’inverse, lorsque nous utilisons le modèle de régression ajusté pour prédire les valeurs de points en dehors de la plage existante, on parle d’ extrapolation :

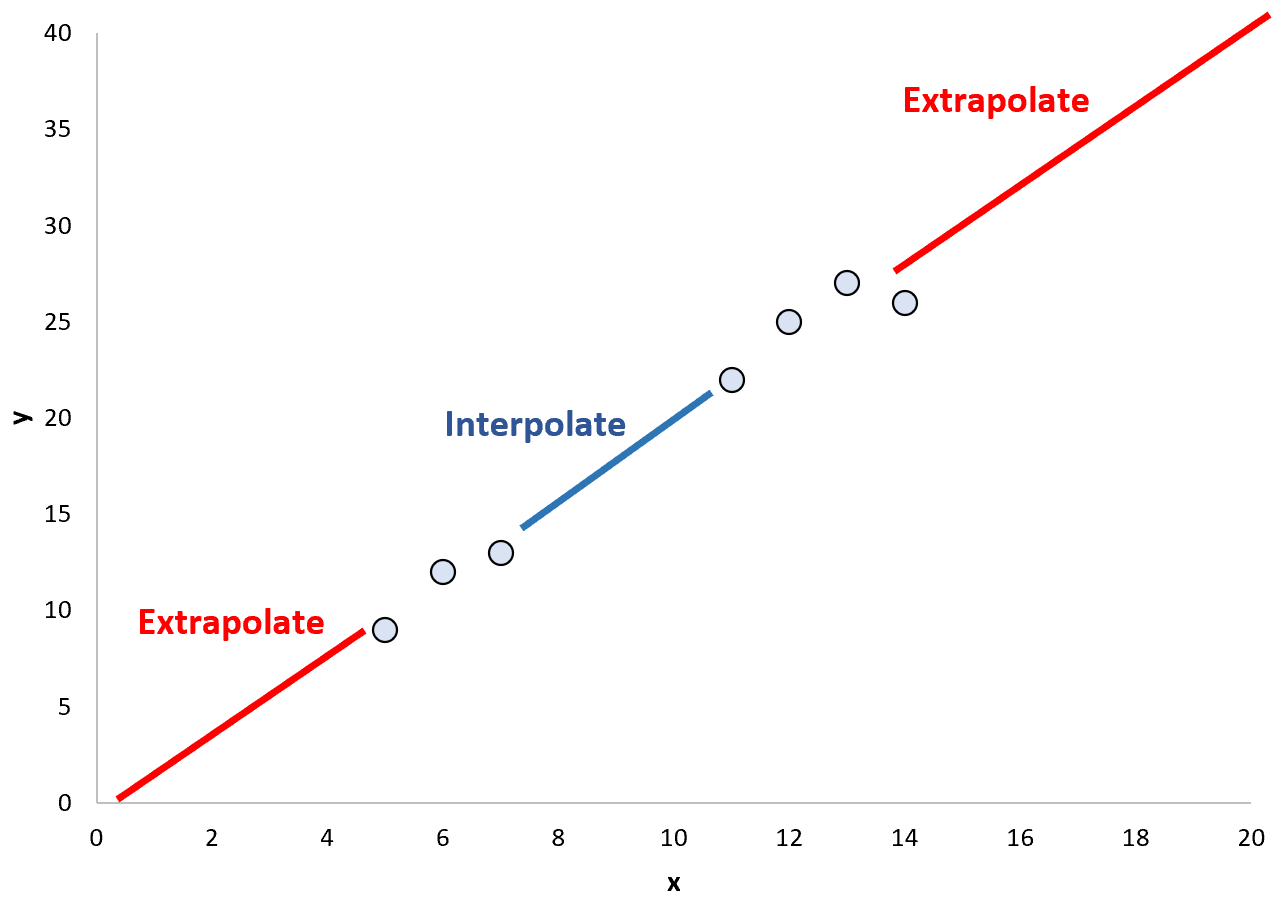
Le danger potentiel de l’extrapolation

Lorsque nous effectuons une extrapolation, nous supposons que le même modèle qui existe à l’intérieur de la plage actuelle de points de données existe également en dehors de la plage.

Cependant, cela peut être une hypothèse dangereuse car il est possible que le modèle qui existe en dehors de la plage actuelle de points de données soit très différent :

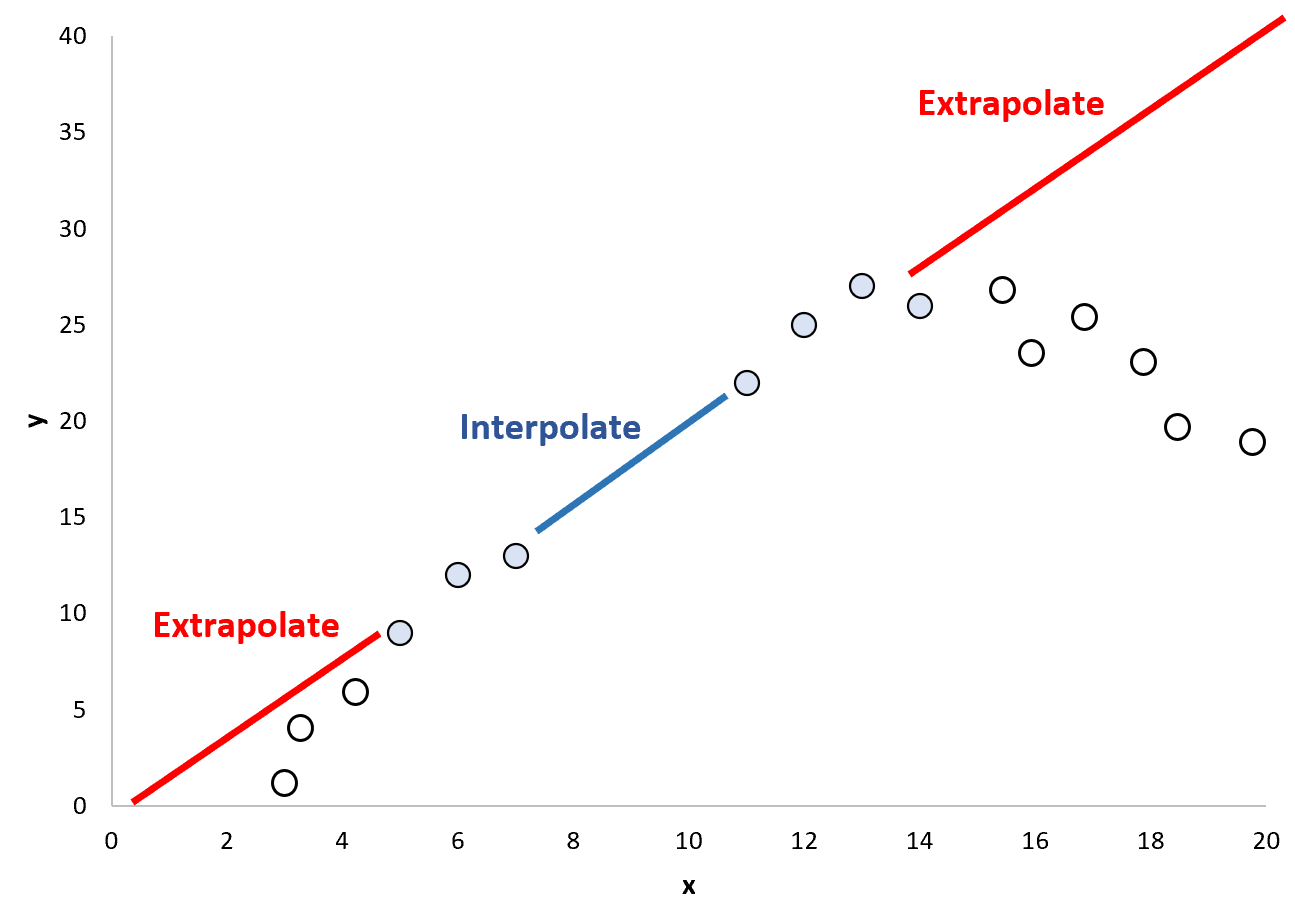
Pour cette raison, il peut être dangereux d’utiliser l’extrapolation pour prédire les valeurs de points de données qui se situent en dehors de la plage de valeurs utilisée pour créer le modèle de régression.

En pratique, il est souvent judicieux d’utiliser l’extrapolation pour prédire les valeurs de points qui se situent légèrement en dehors de la plage des valeurs existantes, mais plus on s’éloigne de la plage, plus il est probable que la différence entre la valeur prédite et la valeur réelle soit importante. .

Quand utiliser l’extrapolation

Il faut souvent une expertise spécifique à un domaine pour déterminer si l’extrapolation est une idée raisonnable ou non.

Par exemple, supposons qu’un service marketing d’une entreprise applique un modèle de régression linéaire simple utilisant les dépenses publicitaires comme variable prédictive et le revenu total comme variable de réponse.

Dans ce scénario, il peut être raisonnable de supposer qu’une augmentation constante des dépenses publicitaires entraînera une augmentation prévisible des revenus totaux :

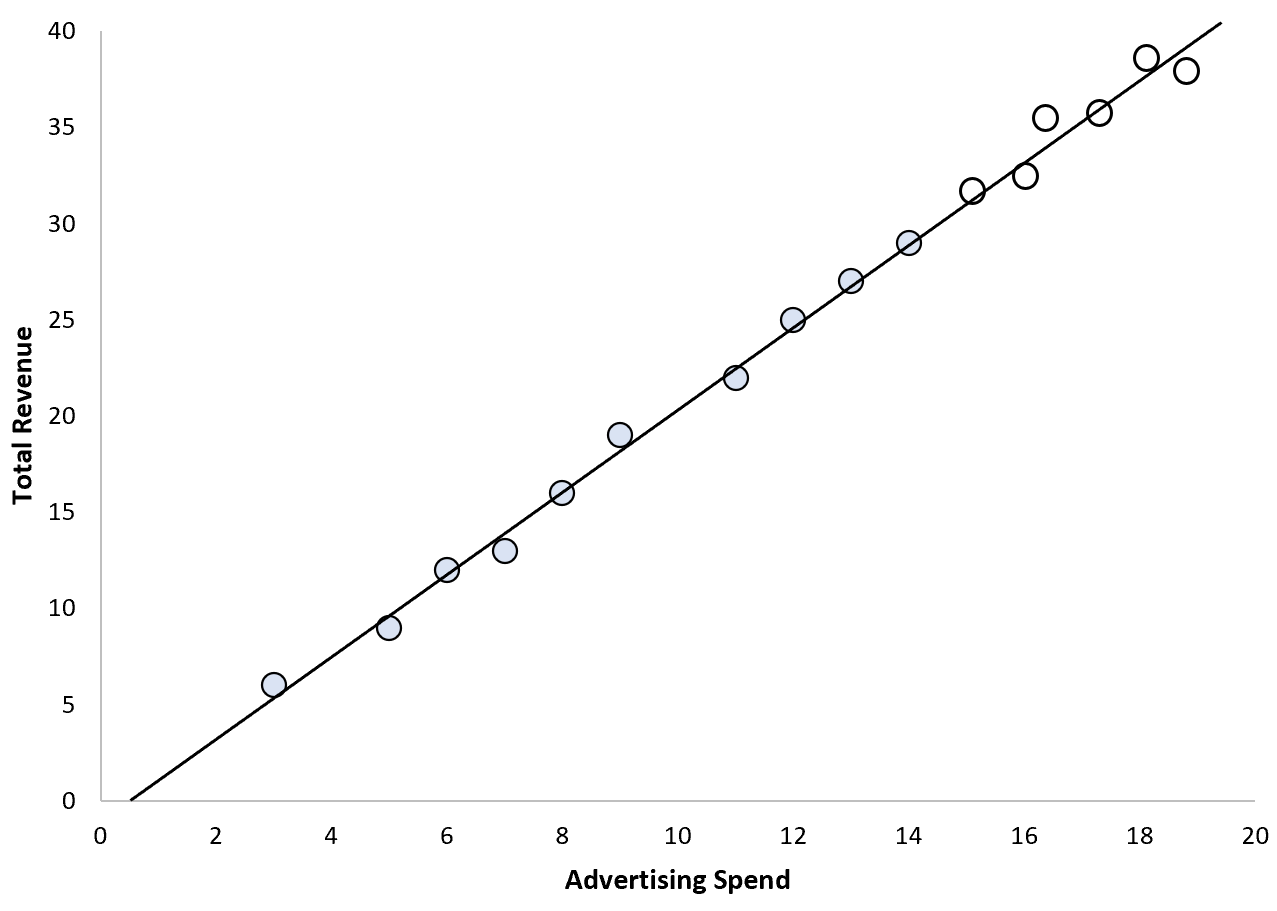
Dans ce scénario, nous pouvons être tout à fait confiants dans notre capacité à extrapoler des valeurs.

Cependant, considérons un scénario dans lequel un biologiste souhaite utiliser un engrais total pour prédire la croissance des plantes.

Elle peut décider d’adapter un simple modèle de régression linéaire aux points de données, mais comme il existe une limite supérieure à la hauteur des plantes, cela n’a probablement pas de sens d’utiliser l’extrapolation pour prédire les valeurs des points en dehors de la plage de valeurs. valeurs utilisées pour ajuster le modèle :

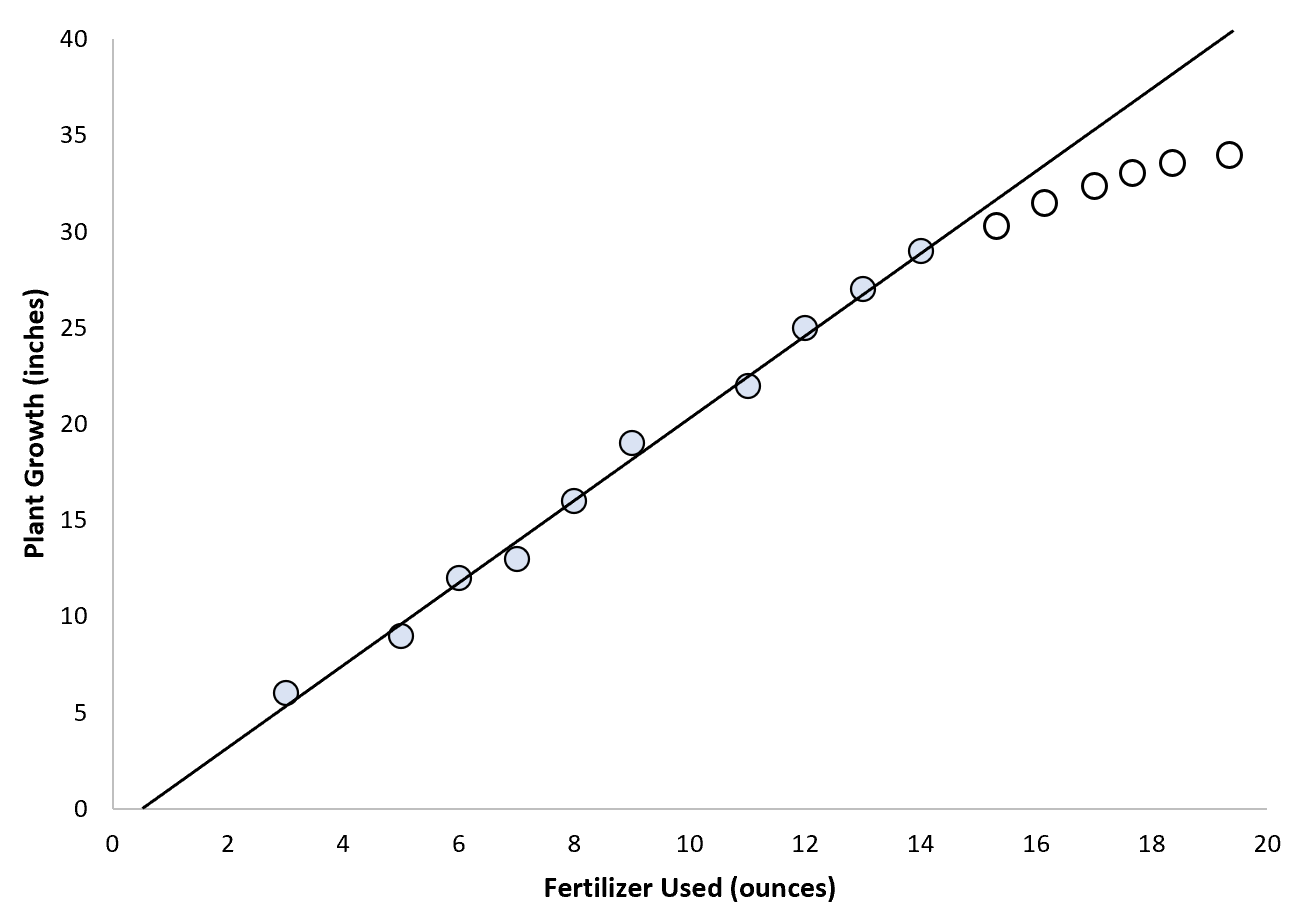
Dans ce scénario, nous pourrions avoir beaucoup moins confiance dans notre capacité à extrapoler des valeurs.

Ce qu’il faut retenir : L’extrapolation peut avoir plus de sens dans certains domaines que dans d’autres, mais il existe toujours un danger potentiel que le modèle qui existe dans la plage de valeurs utilisée pour ajuster le modèle n’existe pas en dehors de la plage.

Ressources additionnelles

Comment effectuer une interpolation linéaire dans Excel
Comment faire des prédictions avec la régression linéaire