Comment interpréter une courbe ROC (avec exemples)
La régression logistique est une méthode statistique que nous utilisons pour ajuster un modèle de régression lorsque la variable de réponse est binaire. Pour évaluer dans quelle mesure un modèle de régression logistique s’adapte à un ensemble de données, nous pouvons examiner les deux métriques suivantes :
- Sensibilité : probabilité que le modèle prédise un résultat positif pour une observation alors que le résultat est effectivement positif.
- Spécificité : probabilité que le modèle prédise un résultat négatif pour une observation alors que le résultat est effectivement négatif.
Un moyen simple de visualiser ces deux métriques consiste à créer une courbe ROC , qui est un graphique qui affiche la sensibilité et la spécificité d’un modèle de régression logistique.
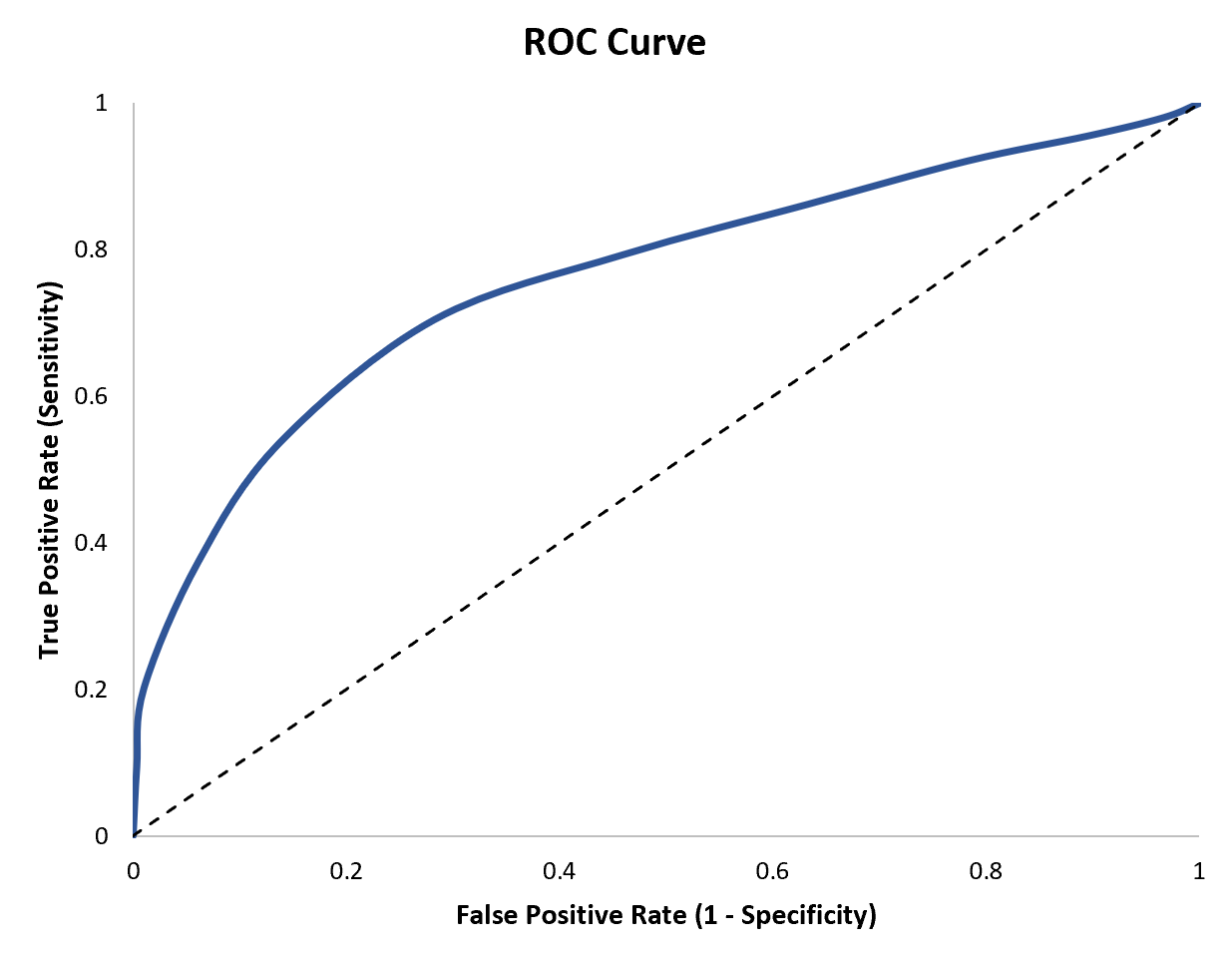
Ce tutoriel explique comment créer et interpréter une courbe ROC.
Comment créer une courbe ROC
Une fois que nous avons ajusté un modèle de régression logistique, nous pouvons utiliser le modèle pour classer les observations dans l’une des deux catégories suivantes.
Par exemple, nous pourrions classer les observations comme « positives » ou « négatives ».
Le taux de vrais positifs représente la proportion d’observations qui devraient être positives alors qu’elles le sont effectivement.
À l’inverse, le taux de faux positifs représente la proportion d’observations qui devraient être positives alors qu’elles sont en réalité négatives.
Lorsque nous créons une courbe ROC, nous traçons les paires du taux de vrais positifs par rapport au taux de faux positifs pour chaque seuil de décision possible d’un modèle de régression logistique.
Comment interpréter une courbe ROC
Plus la courbe ROC épouse le coin supérieur gauche du tracé, plus le modèle parvient à classer les données en catégories.
Pour quantifier cela, nous pouvons calculer l’ AUC (aire sous la courbe) qui nous indique quelle partie de la parcelle est située sous la courbe.
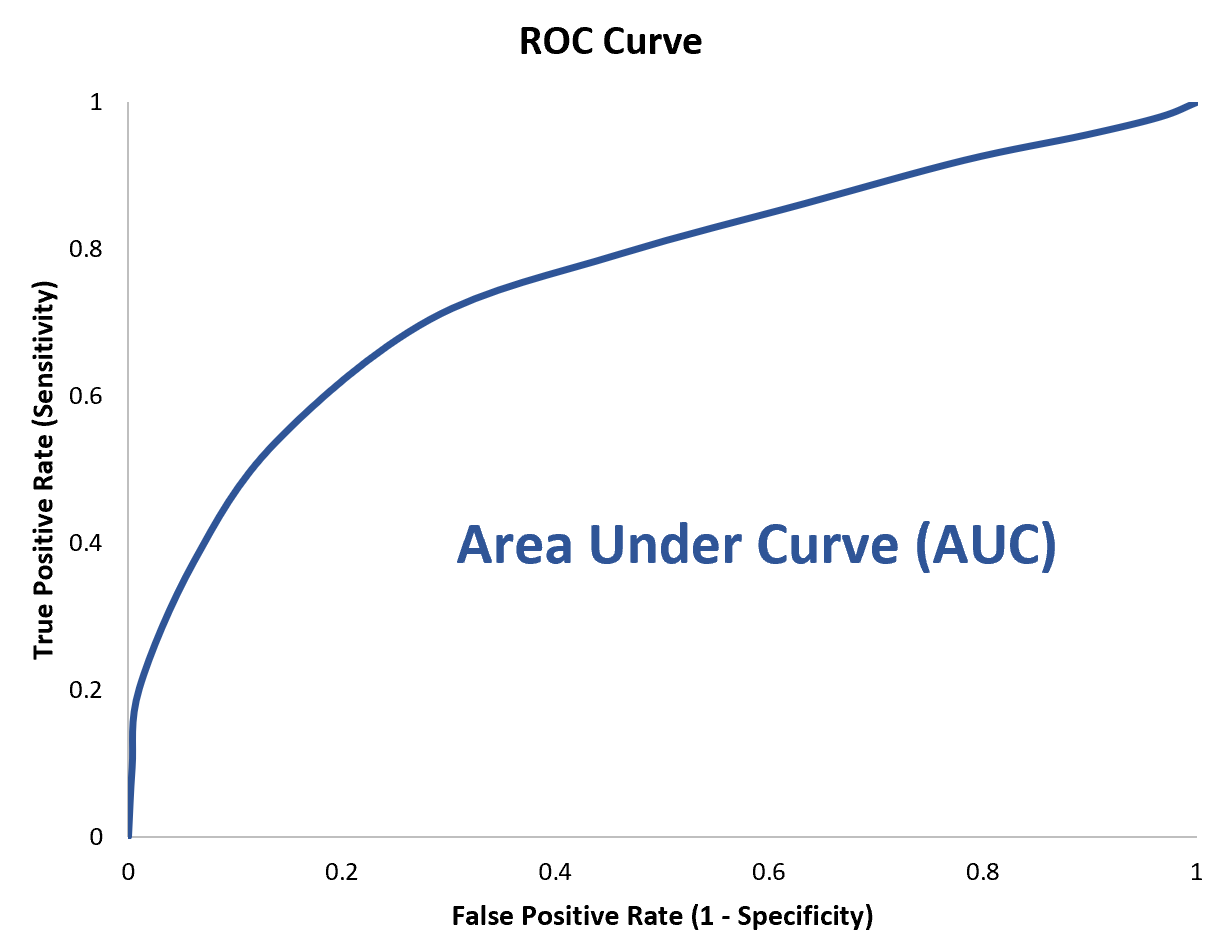
Plus l’AUC est proche de 1, meilleur est le modèle.
Un modèle avec une AUC égale à 0,5 serait une ligne parfaitement diagonale et représenterait un modèle qui ne vaut pas mieux qu’un modèle faisant des classifications aléatoires.
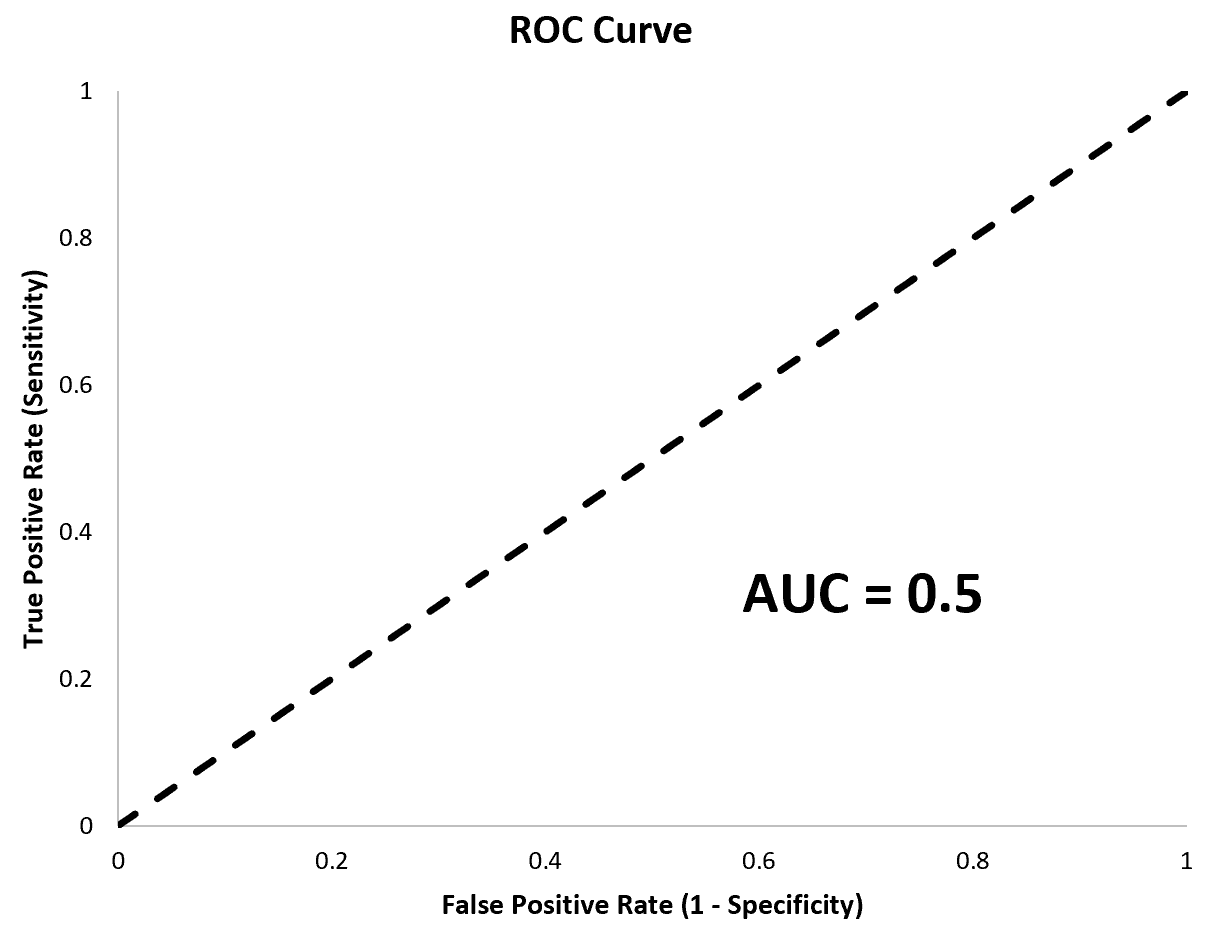
Il est particulièrement utile de calculer l’AUC pour les modèles de régression logistique multiple, car cela nous permet de voir quel modèle est le meilleur pour faire des prédictions.
Par exemple, supposons que nous ajustions trois modèles de régression logistique différents et traçons les courbes ROC suivantes pour chaque modèle :
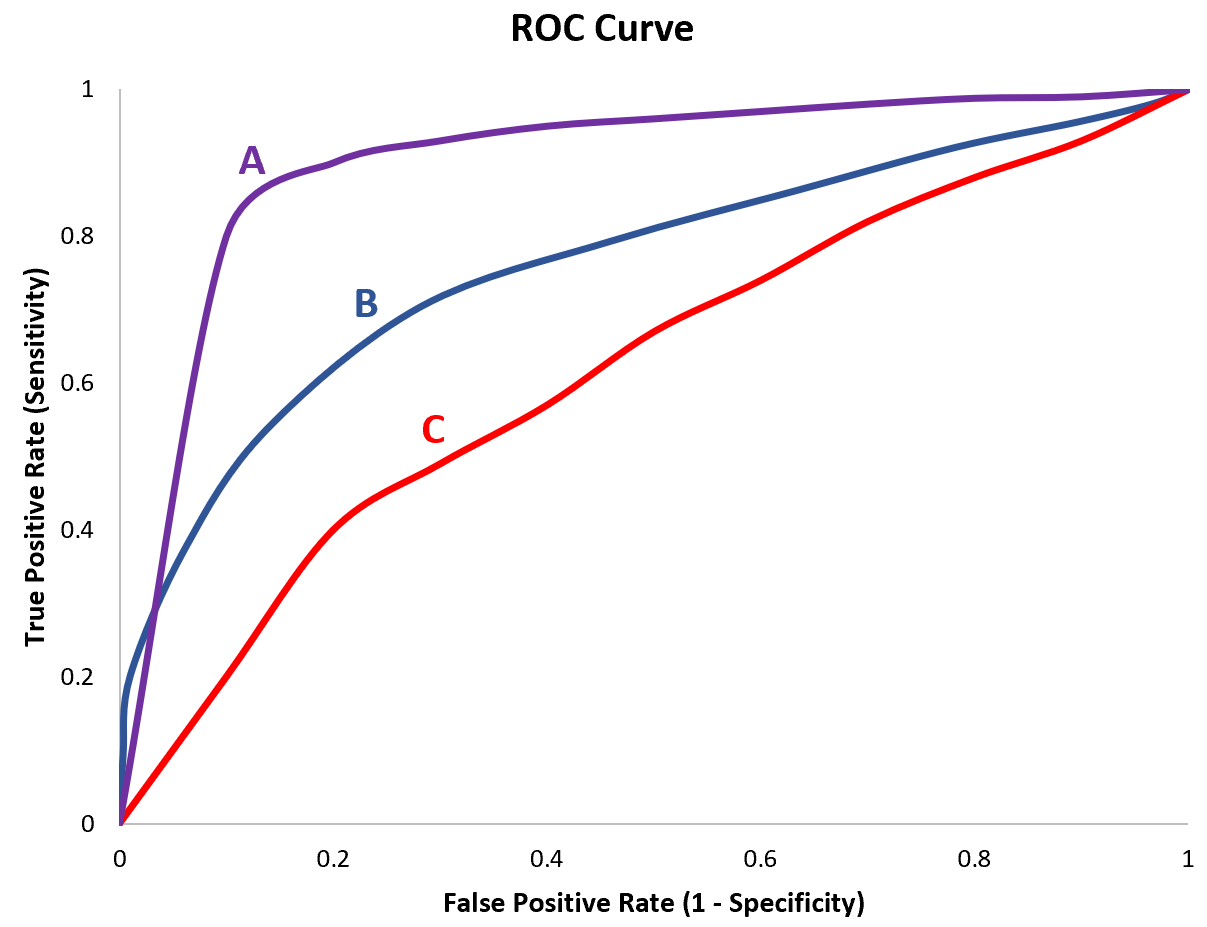
Supposons que nous calculions l’AUC pour chaque modèle comme suit :
- Modèle A : AUC = 0,923
- Modèle B : AUC = 0,794
- Modèle C : AUC = 0,588
Le modèle A a l’AUC la plus élevée, ce qui indique qu’il a l’aire sous la courbe la plus élevée et qu’il constitue le meilleur modèle pour classer correctement les observations en catégories.
Ressources additionnelles
Les tutoriels suivants expliquent comment créer des courbes ROC à l’aide de différents logiciels statistiques :
à propos de l'auteur
Dr. Benjamin Anderson
Il est un professeur de statistiques à la retraite devenu éducateur dévoué sur Statorials. Avec une vaste expérience et une expertise dans le domaine des statistiques, je m'engage à partager mes connaissances pour responsabiliser les étudiants grâce à Statorials. Lire plus