Comment interpréter les valeurs de log-vraisemblance (avec exemples)

La valeur de log de vraisemblance d’un modèle de régression est un moyen de mesurer la qualité de l’ajustement d’un modèle. Plus la valeur de la log-vraisemblance est élevée, plus le modèle s’adapte à un ensemble de données.

La valeur du log de vraisemblance pour un modèle donné peut aller de l’infini négatif à l’infini positif. La valeur réelle du log de vraisemblance pour un modèle donné n’a généralement aucune signification, mais elle est utile pour comparer deux modèles ou plus .

En pratique, nous adaptons souvent plusieurs modèles de régression à un ensemble de données et choisissons le modèle avec la valeur de log-vraisemblance la plus élevée comme modèle qui correspond le mieux aux données.

L’exemple suivant montre comment interpréter les valeurs de log-vraisemblance pour différents modèles de régression dans la pratique.

Exemple : Interprétation des valeurs de log-vraisemblance

Supposons que nous ayons l’ensemble de données suivant qui montre le nombre de chambres, le nombre de salles de bains et le prix de vente de 20 maisons différentes dans un quartier particulier :

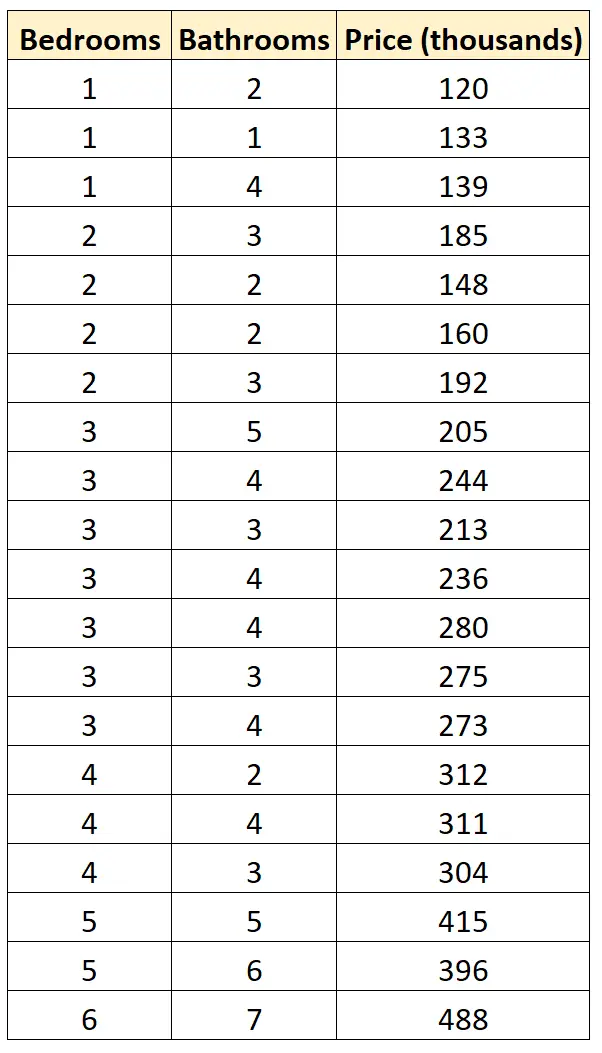
Supposons que nous souhaitions ajuster les deux modèles de régression suivants et déterminer lequel offre le meilleur ajustement aux données :

Modèle 1 : Prix = β ₀ + β ₁ (nombre de chambres)

Modèle 2 : Prix = β ₀ + β ₁ (nombre de salles de bain)

Le code suivant montre comment ajuster chaque modèle de régression et calculer la valeur de log-vraisemblance de chaque modèle dans R :

#define data
df <- data.frame(beds=c(1, 1, 1, 2, 2, 2, 2, 3, 3, 3,
                        3, 3, 3, 3, 4, 4, 4, 5, 5, 6),
                 baths=c(2, 1, 4, 3, 2, 2, 3, 5, 4, 3,
                         4, 4, 3, 4, 2, 4, 3, 5, 6, 7),
                 price=c(120, 133, 139, 185, 148, 160, 192, 205, 244, 213,
                         236, 280, 275, 273, 312, 311, 304, 415, 396, 488))

#fit models
model1 <- lm(price~beds, data=df)
model2 <- lm(price~baths, data=df)

#calculate log-likelihood value of each model
logLik(model1)

'log Lik.' -91.04219 (df=3)

logLik(model2)

'log Lik.' -111.7511 (df=3)

Le premier modèle a une valeur de log de vraisemblance plus élevée ( -91,04 ) que le deuxième modèle ( -111,75 ), ce qui signifie que le premier modèle offre un meilleur ajustement aux données.

Précautions concernant l’utilisation des valeurs de log-vraisemblance

Lors du calcul des valeurs de log de vraisemblance, il est important de noter que l’ajout de variables prédictives supplémentaires à un modèle augmentera presque toujours la valeur de log de vraisemblance, même si les variables prédictives supplémentaires ne sont pas statistiquement significatives.

Cela signifie que vous ne devez comparer les valeurs de log de vraisemblance entre deux modèles de régression que si chaque modèle a le même nombre de variables prédictives.

Pour comparer des modèles avec différents nombres de variables prédictives, vous pouvez effectuer un test de rapport de vraisemblance pour comparer la qualité de l’ajustement de deux modèles de régression imbriqués.

Ressources additionnelles

Comment utiliser la fonction lm() pour ajuster des modèles linéaires dans R
Comment effectuer un test de rapport de vraisemblance dans R