Comment interpréter le V de Cramer (avec exemples)
Le V de Cramer est une mesure de la force de l’association entre deux variables nominales .
Il va de 0 à 1 où :
- 0 indique aucune association entre les deux variables.
- 1 indique une association parfaite entre les deux variables.
Il est calculé comme suit :
V de Cramer = √ (X 2 /n) / min(c-1, r-1)
où:
- X 2 : La statistique du Chi carré
- n : taille totale de l’échantillon
- r : Nombre de lignes
- c : Nombre de colonnes
Comment interpréter le V de Cramer
Le tableau suivant montre comment interpréter le V de Cramer en fonction des degrés de liberté :
| Degrés de liberté | Petit | Moyen | Grand |
|---|---|---|---|
| 1 | 0,10 | 0,30 | 0,50 |
| 2 | 0,07 | 0,21 | 0,35 |
| 3 | 0,06 | 0,17 | 0,29 |
| 4 | 0,05 | 0,15 | 0,25 |
| 5 | 0,04 | 0,13 | 0,22 |
Les exemples suivants montrent comment interpréter le V de Cramer dans différentes situations.
Exemple 1 : Interprétation du V de Cramer pour un tableau 2×3
Supposons que nous voulions savoir s’il existe une association entre la couleur des yeux et le sexe. Nous interrogeons donc 50 personnes et obtenons les résultats suivants :
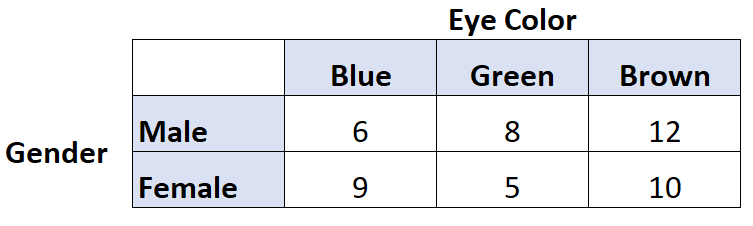
Nous pouvons utiliser le code suivant dans R pour calculer le V de Cramer pour ces deux variables :
library(rcompanion) #create table data = matrix(c(6, 9, 8, 5, 12, 10), nrow=2) #view table data [,1] [,2] [,3] [1,] 6 8 12 [2,] 9 5 10 #calculate Cramer's V cramerV(data) Cramer V 0.1671
Le V de Cramer s’avère être 0,1671 .
Les degrés de liberté seraient calculés comme suit :
- df = min(#lignes-1, #colonnes-1)
- df = min(1, 2)
- df = 1
En nous référant au tableau ci-dessus, nous pouvons voir qu’un V de Cramer de 0,1671 et des degrés de liberté = 1 indiquent une petite (ou « faible ») association entre la couleur des yeux et le sexe.
Exemple 2 : Interprétation du V de Cramer pour une table 3×3
Supposons que nous voulions savoir s’il existe une association entre la couleur des yeux et la préférence pour un parti politique. Nous interrogeons donc 50 personnes et obtenons les résultats suivants :
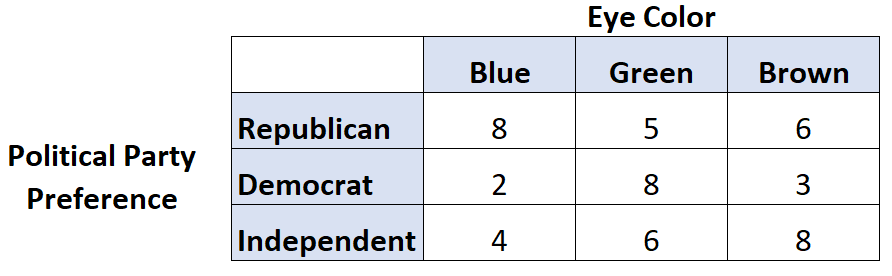
Nous pouvons utiliser le code suivant dans R pour calculer le V de Cramer pour ces deux variables :
library(rcompanion) #create table data = matrix(c(8, 2, 4, 5, 8, 6, 6, 3, 8), nrow=3) #view table data [,1] [,2] [,3] [1,] 8 5 6 [2,] 2 8 3 [3,] 4 6 8 #calculate Cramer's V cramerV(data) Cramer V 0.246
Le V de Cramer s’avère être 0,246 .
Les degrés de liberté seraient calculés comme suit :
- df = min(#lignes-1, #colonnes-1)
- df = min(2, 2)
- df = 2
En nous référant au tableau ci-dessus, nous pouvons voir qu’un V de Cramer de 0,246 et des degrés de liberté = 2 indiquent une association moyenne (ou « modérée ») entre la couleur des yeux et la préférence pour un parti politique.
Ressources additionnelles
Les tutoriels suivants expliquent comment calculer le V de Cramer dans différents logiciels statistiques :
Comment calculer le V de Cramer dans Excel
Comment calculer le V de Cramer dans R
Comment calculer le V de Cramer en Python
