Comment calculer un intervalle de confiance de Poisson (étape par étape)

La distribution de Poisson est une distribution de probabilité utilisée pour modéliser la probabilité qu’un certain nombre d’événements se produisent pendant un intervalle de temps fixe lorsque l’on sait que les événements se produisent indépendamment et avec un taux moyen constant.

S’il est utile de connaître le nombre moyen d’occurrences d’un processus de Poisson, il peut être encore plus utile d’avoir un intervalle de confiance autour du nombre moyen d’occurrences.

Par exemple, supposons que nous collectons des données dans un centre d’appels un jour aléatoire et que nous constatons que le nombre moyen d’appels par heure est de 15.

Comme nous n’avons collecté les données que sur une seule journée, nous ne pouvons pas être sûrs que le centre d’appels reçoive en moyenne 15 appels par heure tout au long de l’année.

Cependant, nous pouvons utiliser la formule suivante pour calculer un intervalle de confiance pour le nombre moyen d’appels par heure :

Formule d’intervalle de confiance de Poisson

Intervalle de confiance = [0,5*X ² _{2N, α/2} , 0,5*X ² _{2(N+1), 1-α/2} ]

où:

• X ² : Valeur critique du chi carré
• N : Le nombre d’événements observés
• α : le niveau de signification

L’exemple suivant, étape par étape, illustre comment calculer un intervalle de confiance de Poisson à 95 % dans la pratique.

Étape 1 : compter les événements observés

Supposons que nous calculions le nombre moyen d’appels par heure dans un centre d’appels à 15. Ainsi, N = 15 .

Et puisque nous calculons un intervalle de confiance de 95 %, nous utiliserons α = 0,05 dans les calculs suivants.

Étape 2 : Trouver la limite inférieure de l’intervalle de confiance

La limite inférieure de l’intervalle de confiance est calculée comme suit :

• Limite inférieure = 0,5*X ² _{2N, α/2}
• Limite inférieure = 0,5*X ² _{2(15), 0,975}
• Limite inférieure = 0,5*X ² _{30, 0,975}
• Limite inférieure = 0,5*16,791
• Limite inférieure = 8,40

Remarque : Nous avons utilisé le calculateur de valeur critique du chi carré pour calculer X ² _{30, 0,975} .

Étape 3 : Trouver la limite supérieure de l’intervalle de confiance

La limite supérieure de l’intervalle de confiance est calculée comme suit :

• Limite supérieure = 0,5*X ² _{2(N+1), 1-α/2}
• Limite supérieure = 0,5*X ² _{2(15+1), 0,025}
• Limite supérieure = 0,5*X ² _{32, 0,025}
• Limite supérieure = 0,5*49,48
• Limite supérieure = 24,74

Remarque : Nous avons utilisé le calculateur de valeur critique du chi carré pour calculer X ² _{32, 0,025} .

Étape 4 : Trouver l’intervalle de confiance

En utilisant les limites inférieure et supérieure calculées précédemment, notre intervalle de confiance de Poisson à 95 % s’avère être :

• IC à 95 % = [8,40, 24,74]

Cela signifie que nous sommes sûrs à 95 % que le nombre moyen réel d’appels par heure que le centre d’appels reçoit se situe entre 8,40 appels et 24,74 appels.

Bonus : Calculateur d’intervalle de confiance de Poisson

N’hésitez pas à utiliser ce calculateur d’intervalle de confiance de Poisson pour calculer automatiquement un intervalle de confiance de Poisson.

Par exemple, voici comment utiliser cette calculatrice pour trouver l’intervalle de confiance de Poisson que nous venons de calculer manuellement :

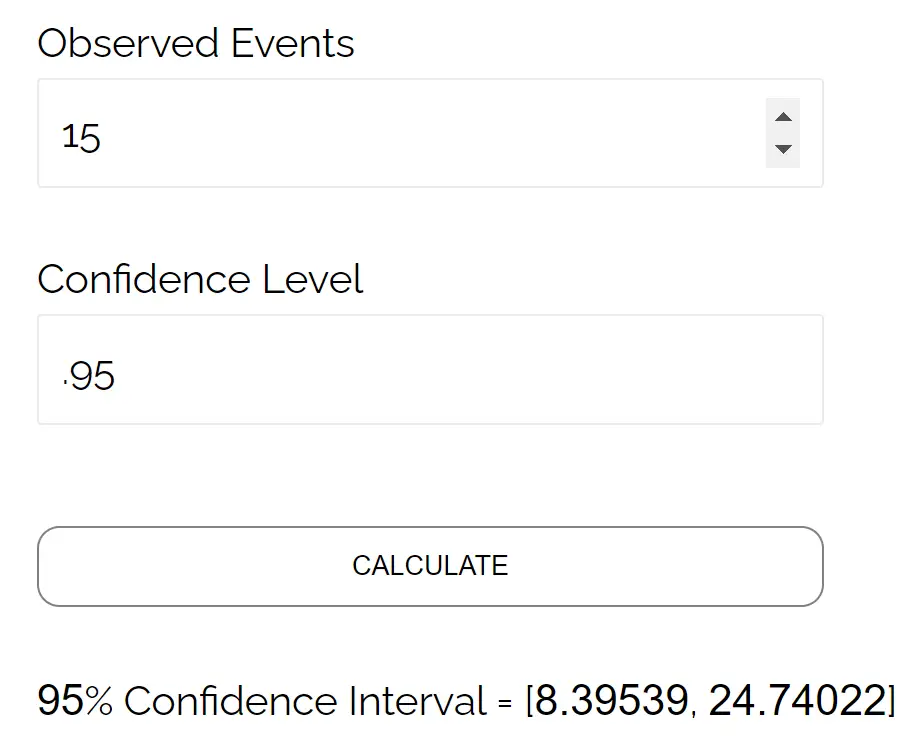
Notez que les résultats correspondent à l’intervalle de confiance que nous avons calculé manuellement.