Intervalle de confiance pour la différence entre les moyennes

Un intervalle de confiance (IC) pour une différence entre des moyennes est une plage de valeurs susceptible de contenir la véritable différence entre deux moyennes de population avec un certain niveau de confiance.

Ce tutoriel explique les éléments suivants :

• La motivation pour créer cet intervalle de confiance.
• La formule pour créer cet intervalle de confiance.
• Un exemple de la façon de calculer cet intervalle de confiance.
• Comment interpréter cet intervalle de confiance.

IC pour la différence entre les moyens : motivation

Les chercheurs souhaitent souvent estimer la différence entre les moyennes de deux populations. Pour estimer cette différence, ils vont rassembler un échantillon aléatoire de chaque population et calculer la moyenne pour chaque échantillon. Ensuite, ils peuvent comparer la différence entre les deux moyennes.

Cependant, ils ne peuvent pas savoir avec certitude si la différence entre les moyennes de l’échantillon correspond à la véritable différence entre les moyennes de la population. C’est pourquoi ils peuvent créer un intervalle de confiance pour la différence entre les deux moyennes. Cela fournit une plage de valeurs susceptible de contenir la véritable différence entre les moyennes de la population.

Par exemple, supposons que nous souhaitions estimer la différence de poids moyen entre deux espèces différentes de tortues. Comme il y a des milliers de tortues dans chaque population, il serait trop long et coûteux de faire le tour et de peser chaque tortue individuellement.

Au lieu de cela, nous pourrions prendre un échantillon aléatoire simple de 15 tortues de chaque population et utiliser le poids moyen de chaque échantillon pour estimer la véritable différence de poids moyen entre les deux populations :

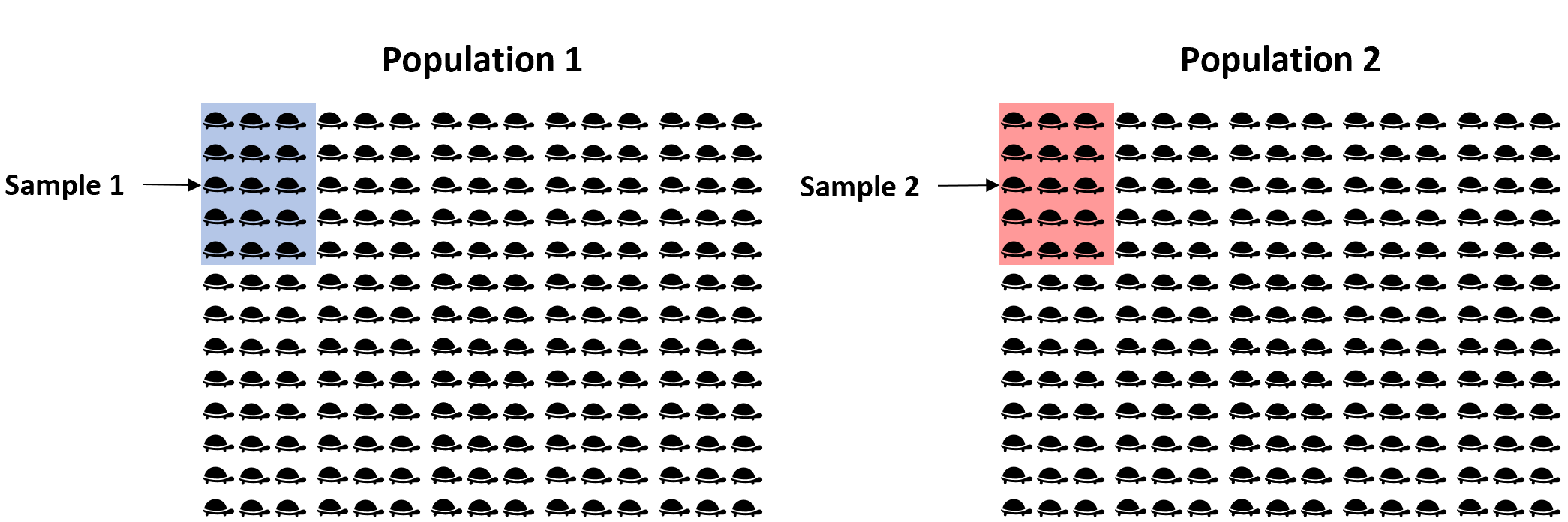
Le problème est que nos échantillons sont aléatoires, donc il n’est pas garanti que la différence de poids moyen entre les deux échantillons corresponde exactement à la différence de poids moyen entre les deux populations. Ainsi, pour capturer cette incertitude, nous pouvons créer un intervalle de confiance contenant une plage de valeurs susceptibles de contenir la véritable différence de poids moyen entre les deux populations.

IC pour la différence entre les moyennes : formule

Nous utilisons la formule suivante pour calculer un intervalle de confiance pour une différence entre deux moyennes :

Intervalle de confiance = ( x ₁ – x ₂ ) +/- t*√((s _p ² /n ₁ ) + (s _p ² /n ₂ ))

où:

• x ₁ , x ₂ : moyenne de l’échantillon 1, moyenne de l’échantillon 2
• t : la valeur t-critique basée sur le niveau de confiance et (n ₁ + n ₂ -2) degrés de liberté
• s _p ² : variance poolée
• n ₁ , n ₂ : taille de l’échantillon 1, taille de l’échantillon 2

où:

• La variance groupée est calculée comme suit : s _p ² = ((n ₁ -1)s ₁ ² + (n ₂ -1)s ₂ ² ) / (n ₁ +n ₂ -2)
• La valeur t-critique t peut être trouvée à l’aide du calculateur de distribution t inverse.

IC pour la différence entre les moyennes : exemple

Supposons que nous voulions estimer la différence de poids moyen entre deux espèces différentes de tortues. Nous allons donc rassembler un échantillon aléatoire de 15 tortues de chaque population. Voici les données récapitulatives pour chaque échantillon :

Échantillon 1 :

• x1 = ₃₁₀
• s ₁ = 18,5
• n ₁ = 15

Échantillon 2 :

• x2 ₌ 300
• s ₂ = 16,4
• _n2 = 15

Voici comment trouver différents intervalles de confiance pour la véritable différence dans les poids moyens de la population :

Intervalle de confiance à 90 % :

(310-300) +/- 1,70*√((305,61/15) + (305,61/15)) = [-0,8589, 20,8589]

Intervalle de confiance à 95 % :

(310-300) +/- 2,05*√((305,61/15) + (305,61/15)) = [-3,0757, 23,0757]

Intervalle de confiance à 99 % :

(310-300) +/- 2,76*√((305,61/15) + (305,61/15)) = [-7,6389, 27,6389]

Remarque : Vous pouvez également trouver ces intervalles de confiance à l’aide de l’ Intervalle de confiance statistique pour le calculateur de différence entre les moyennes .

Vous remarquerez que plus le niveau de confiance est élevé, plus l’intervalle de confiance est large. Cela devrait avoir du sens, car des intervalles plus larges sont plus susceptibles de contenir la véritable moyenne de la population, nous sommes donc plus « confiants » que l’intervalle contient la véritable moyenne de la population.

IC pour la différence entre les moyennes : interprétation

La façon dont nous interpréterions un intervalle de confiance est la suivante :

Il y a 95 % de chances que l’intervalle de confiance de [-3,0757, 23,0757] contienne la véritable différence de poids moyen entre les deux populations de tortues.

Puisque cet intervalle contient la valeur « 0 », cela signifie qu’il est possible qu’il n’y ait pas de différence de poids moyen entre les tortues de ces deux populations. En d’autres termes, nous ne pouvons pas affirmer avec un degré de confiance de 95 % qu’il existe une différence de poids moyen entre les tortues de ces deux populations.