Excel : calculer l’intervalle de confiance pour le coefficient de régression

Dans un modèle de régression linéaire, un coefficient de régression nous indique la variation moyenne de la variable de réponse associée à une augmentation d’une unité de la variable prédictive.

Nous pouvons utiliser la formule suivante pour calculer un intervalle de confiance pour un coefficient de régression :

Intervalle de confiance pour β ₁ : b ₁ ± t _{1-α/2, n-2} * se(b ₁ )

où:

•   b ₁ = Coefficient de régression indiqué dans le tableau de régression
• t _{1-∝/2, n-2} = La valeur critique t pour le niveau de confiance 1-∝ avec n-2 degrés de liberté où n est le nombre total d’observations dans notre ensemble de données
• se(b ₁ ) = L’erreur type de b ₁ indiquée dans le tableau de régression

L’exemple suivant montre comment calculer un intervalle de confiance pour un coefficient de régression dans Excel.

Exemple : intervalle de confiance pour le coefficient de régression dans Excel

Supposons que nous souhaitions ajuster un modèle de régression linéaire simple utilisant les heures étudiées comme variable prédictive et les résultats à l’examen comme variable de réponse pour 15 étudiants d’une classe particulière :

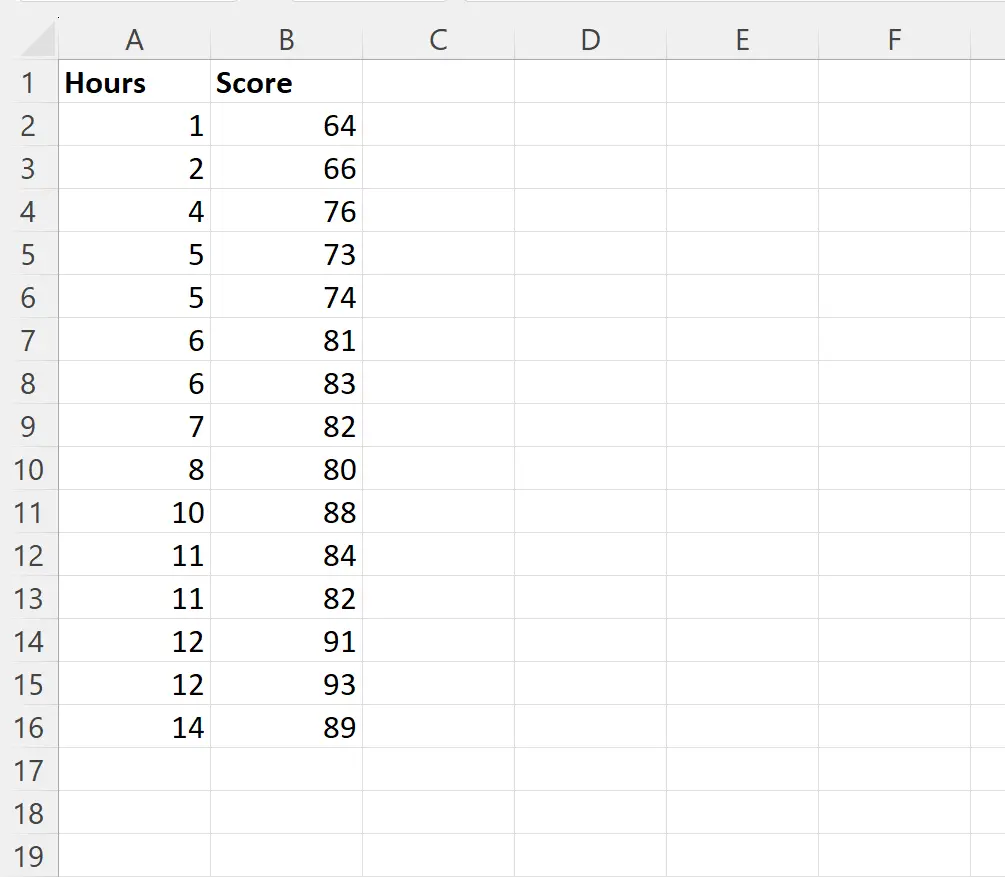
Nous pouvons taper la formule suivante dans la cellule D2 pour effectuer une régression linéaire simple en utilisant les valeurs de la colonne Heures comme variable prédictive et les valeurs de la colonne Score comme variable de réponse :

=LINEST(B2:B16, A2:A16, TRUE, TRUE)

Notez que le premier argument VRAI indique à Excel de calculer normalement l’ordonnée à l’origine de l’équation de régression sans la forcer à être nulle.

Le deuxième argument TRUE indique à Excel de produire des statistiques de régression supplémentaires en plus des coefficients.

La capture d’écran suivante montre le résultat de cette formule (nous expliquons ce que représente chaque valeur de la sortie dans le texte rouge sous la sortie) :

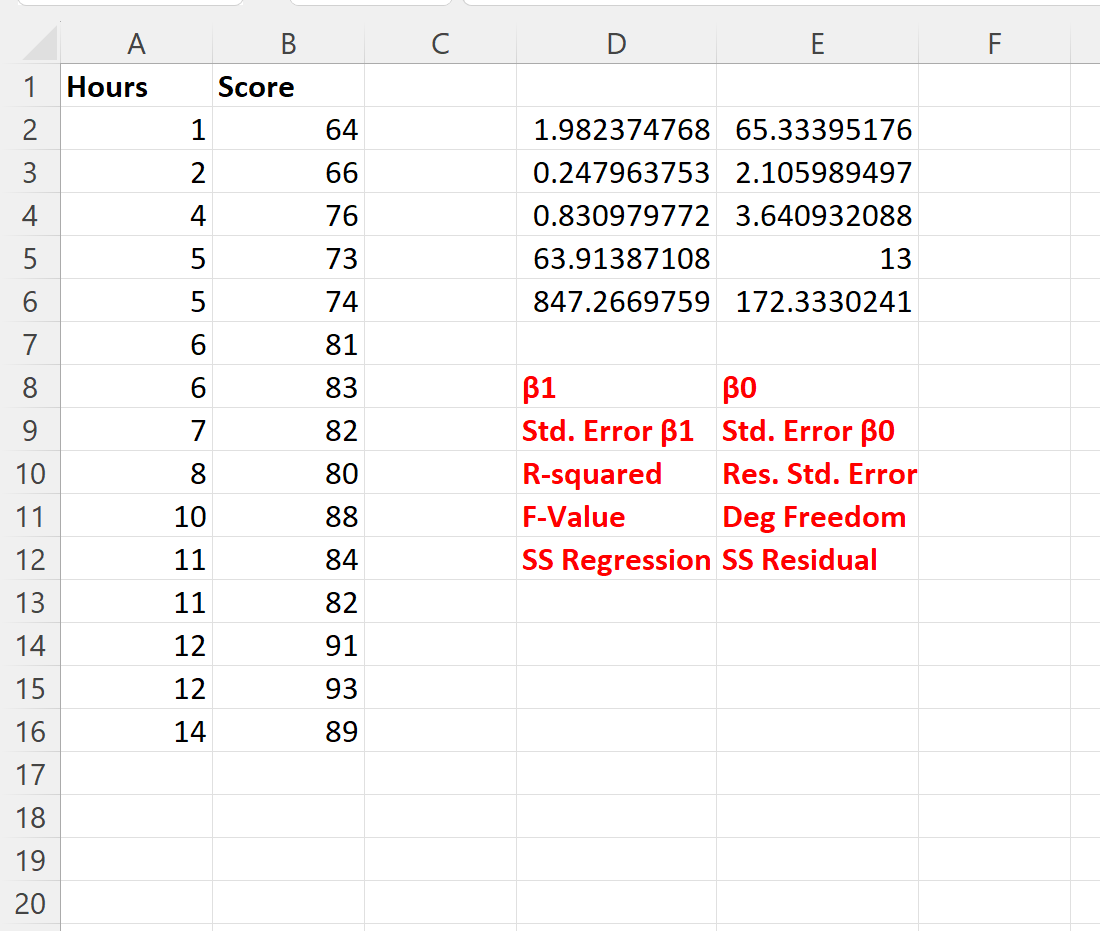
En utilisant les coefficients de régression, nous pouvons écrire l’équation de régression ajustée comme suit :

Score = 65,334 + 1,982*(Heures étudiées)

Notez que le coefficient de régression pour les heures est de 1,982 .

Cela nous indique que chaque heure supplémentaire d’étude consacrée est associée à une augmentation moyenne de 1,982 de la note à l’examen.

Pour calculer un intervalle de confiance à 95 % pour le coefficient de régression, nous pouvons saisir les formules suivantes dans les cellules H2 et H3 :

• H2 : = D2 – T.INV.2T(0,05, E5)*D3
• H3 : = D2 + T.INV.2T(0,05, E5)*D3

La capture d’écran suivante montre comment utiliser ces formules dans la pratique :

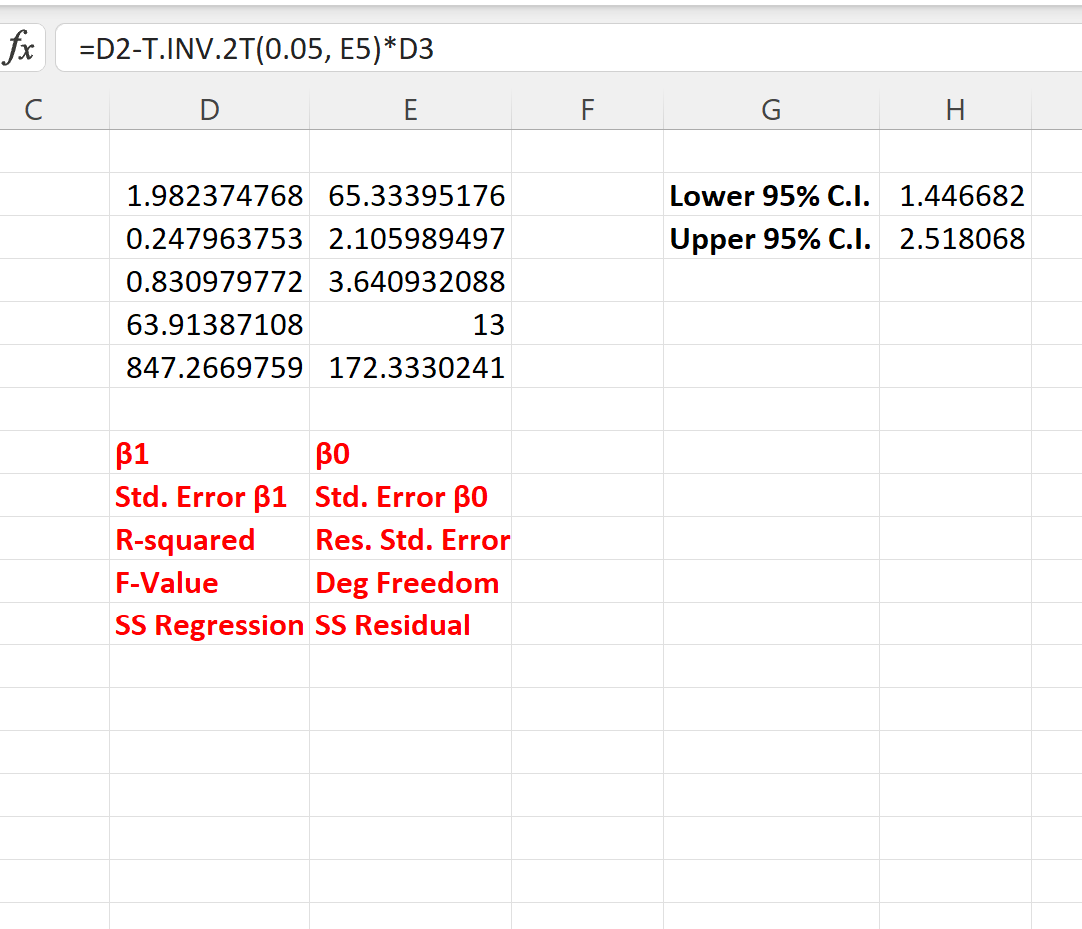
L’intervalle de confiance à 95 % pour le coefficient de régression est [1,446, 2,518] .

Étant donné que cet intervalle de confiance ne contient pas la valeur 0 , nous pouvons conclure qu’il existe une association statistiquement significative entre les heures étudiées et la note à l’examen.

Nous pouvons également confirmer que cela est correct en calculant manuellement l’intervalle de confiance à 95 % pour le coefficient de régression :

• IC à 95 % pour β ₁ : b ₁ ± t _{1-α/2, n-2} * se(b ₁ )
• IC à 95 % pour β ₁ : 1,982 ± t _{0,975, 15-2} * 0,248
• IC à 95 % pour β ₁ : 1,982 ± 2,1604 * 0,248
• IC à 95 % pour β ₁ : [1,446, 2,518]

L’intervalle de confiance à 95 % pour le coefficient de régression est [1,446, 2,518] .

Ressources additionnelles

Les didacticiels suivants expliquent comment effectuer d’autres tâches courantes dans Excel :

Comment effectuer une régression linéaire simple dans Excel
Comment effectuer une régression linéaire multiple dans Excel
Comment interpréter les valeurs P dans la sortie de régression dans Excel