Comment calculer un intervalle de confiance pour le risque relatif

On calcule souvent le risque relatif lors de l’analyse d’un tableau 2×2, qui prend le format suivant :

Le risque relatif nous indique la probabilité qu’un événement se produise dans un groupe de traitement par rapport à la probabilité qu’un événement se produise dans un groupe témoin.

Il est calculé comme suit :

• Risque relatif = [A/(A+B)] / [C/(C+D)]

On peut alors utiliser la formule suivante pour calculer un intervalle de confiance pour le risque relatif (RR) :

• IC inférieur à 95 % = e ^{ln(RR) – 1,96√ 1/a + 1/c – 1/(a+b) – 1/(c+d)}
• IC supérieur à 95 % = e ^{ln(RR) + 1,96√ 1/a + 1/c – 1/(a+b) – 1/(c+d)}

L’exemple suivant montre comment calculer un risque relatif et un intervalle de confiance correspondant dans la pratique.

Exemple : Calcul d’un intervalle de confiance pour le risque relatif

Supposons qu’un entraîneur de basket-ball utilise un nouveau programme d’entraînement pour voir s’il augmente le nombre de joueurs capables de réussir un certain test de compétences, par rapport à un ancien programme d’entraînement.

L’entraîneur recrute 50 joueurs pour utiliser chaque programme. Le tableau suivant montre le nombre de joueurs qui ont réussi et échoué au test d’aptitudes, en fonction du programme qu’ils ont utilisé :

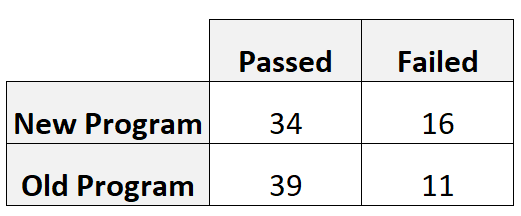
Nous pouvons calculer le risque relatif comme suit :

• Risque relatif = [A/(A+B)] / [C/(C+D)]
• Risque relatif = [34/(34+16)] / [39/(39+11)]
• Risque relatif = 0,8718

Nous interprétons cela comme signifiant que la probabilité qu’un joueur réussisse le test en utilisant le nouveau programme n’est que de 0,8718 fois la probabilité qu’un joueur réussisse le test en utilisant l’ancien programme.

En d’autres termes, la probabilité qu’un joueur réussisse le test est en fait réduite grâce à l’utilisation du nouveau programme.

Nous pouvons alors utiliser les formules suivantes pour calculer l’intervalle de confiance à 95 % pour le risque relatif :

• IC inférieur à 95 % = e ^{ln(.8718) – 1,96√ (1/34 + 1/39 – 1/(34+16) – 1/(39+11)} = 0,686
• IC supérieur à 95 % = e ^{ln(.8718) + 1,96√ (1/34 + 1/39 + 1/(34+16) – 1/(39+11)} = 1,109

Ainsi, l’intervalle de confiance à 95 % pour le risque relatif est de [0,686, 1,109] .

Nous sommes convaincus à 95 % que le véritable risque relatif entre le nouveau et l’ancien programme de formation est contenu dans cet intervalle.

Puisque cet intervalle de confiance contient la valeur 1, il n’est pas statistiquement significatif.

Cela devrait avoir du sens si l’on considère les éléments suivants :

• Un risque relatif supérieur à 1 signifierait que la probabilité qu’un joueur réussisse le test en utilisant le nouveau programme est supérieure à la probabilité qu’un joueur réussisse le test en utilisant l’ancien programme.
• Un risque relatif inférieur à 1 signifierait que la probabilité qu’un joueur réussisse le test en utilisant le nouveau programme est inférieure à la probabilité qu’un joueur réussisse le test en utilisant l’ancien programme.

Ainsi, puisque notre intervalle de confiance à 95 % pour le risque relatif contient la valeur 1, cela signifie que la probabilité qu’un joueur réussisse le test d’aptitudes en utilisant le nouveau programme peut ou non être supérieure à la probabilité que le même joueur réussisse le test en utilisant le nouveau programme. ancien programme.

Ressources additionnelles

Les didacticiels suivants fournissent des informations supplémentaires sur les rapports de cotes et le risque relatif :

Comment interpréter les rapports de cotes
Comment interpréter le risque relatif
Comment calculer le rapport de cotes et le risque relatif dans Excel