Comment construire un intervalle de prédiction dans Excel

En statistique, la régression linéaire simple est une technique que nous pouvons utiliser pour quantifier la relation entre une variable prédictive, x, et une variable de réponse, y.

Lorsque nous effectuons une régression linéaire simple, nous obtenons une « droite de meilleur ajustement » qui décrit la relation entre x et y, qui peut s’écrire :

ŷ = b ₀ + b ₁ x

où:

• ŷ est la valeur prédite de la variable de réponse
• b ₀ est l’ordonnée à l’origine
• b ₁ est le coefficient de régression
• x est la valeur de la variable prédictive

Parfois, nous souhaitons utiliser cette ligne de meilleur ajustement pour construire un intervalle de prédiction pour une valeur donnée de x ₀ , qui est un intervalle autour de la valeur prédite ŷ ₀ tel qu’il y ait une probabilité de 95 % que la valeur réelle de y dans la population correspondant à x ₀ est comprise dans cet intervalle.

La formule pour calculer l’intervalle de prédiction pour une valeur donnée x ₀ s’écrit :

ŷ ₀ +/- t _α/2,df=n-2 * se

où:

se = S _yx √(1 + 1/n + (x ₀ – x ) ² /SS _x )

La formule peut paraître un peu intimidante, mais elle est en réalité simple à calculer dans Excel. Nous verrons ensuite un exemple d’utilisation de cette formule pour calculer un intervalle de prédiction pour une valeur donnée dans Excel.

Exemple : Comment construire un intervalle de prédiction dans Excel

L’ensemble de données suivant montre le nombre d’heures étudiées ainsi que la note d’examen obtenue par 15 étudiants différents :

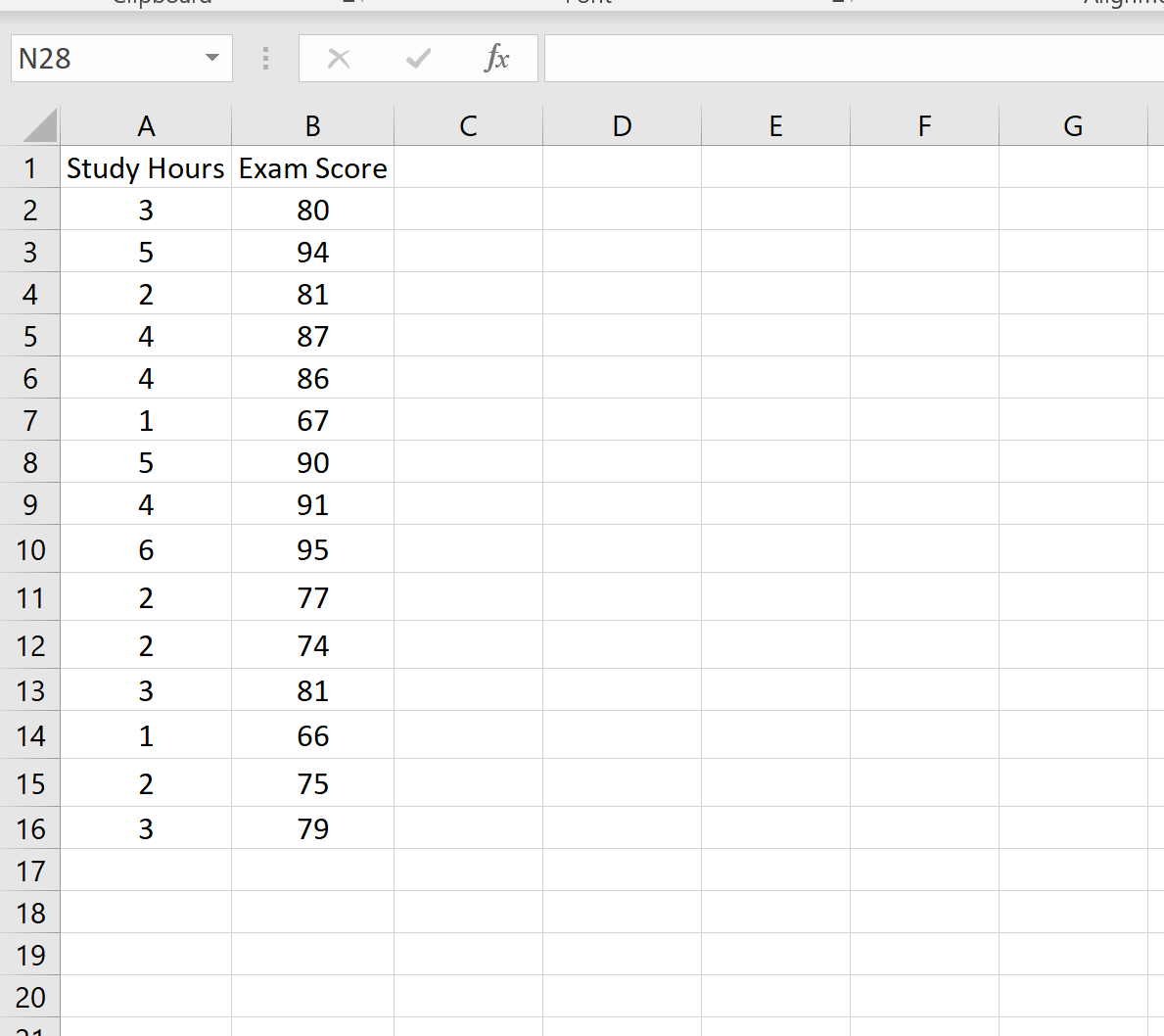
Supposons que nous souhaitions créer un intervalle de prédiction de 95 % pour la valeur x ₀ = 3. Autrement dit, nous souhaitons créer un intervalle tel qu’il y ait une probabilité de 95 % que la note de l’examen se situe dans cet intervalle pour un étudiant qui étudie pour 3 heures.

La capture d’écran suivante montre comment calculer toutes les valeurs nécessaires pour obtenir cet intervalle de prédiction.

Remarque : Les formules de la colonne F montrent comment les valeurs de la colonne E ont été calculées.

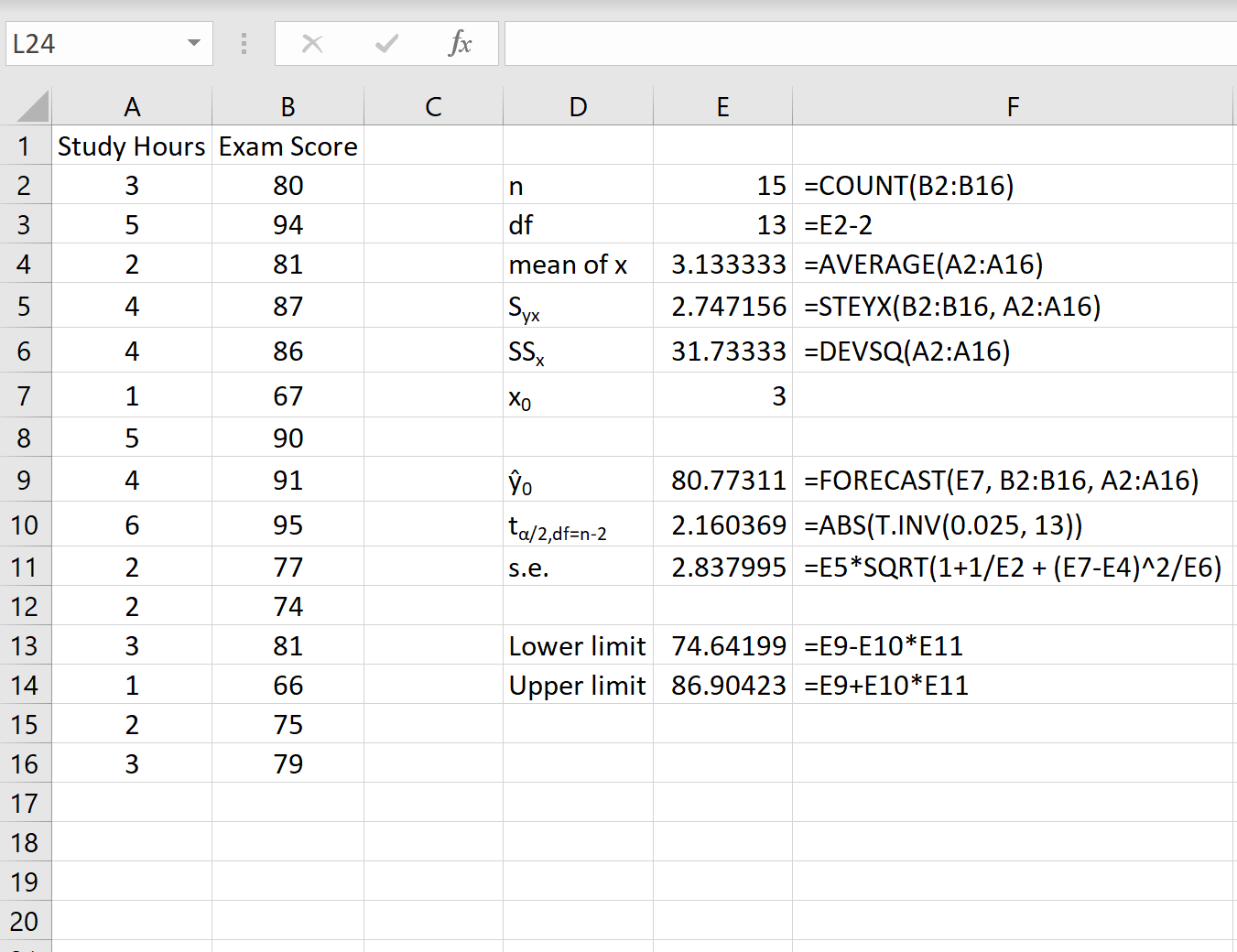
L’intervalle de prédiction de 95 % pour une valeur de x ₀ = 3 est (74,64, 86,90) . Autrement dit, nous prédisons avec une probabilité de 95 % qu’un étudiant qui étudie pendant 3 heures obtiendra un score compris entre 74,64 et 86,90.

Quelques notes sur les calculs utilisés :

• Pour calculer la valeur t-critique de t _α/2,df=n-2, nous avons utilisé α/2 = 0,05/2 = 0,25 puisque nous voulions un intervalle de prédiction de 95 %. Notez que des intervalles de prédiction plus élevés (par exemple, intervalle de prédiction de 99 %) conduiront à des intervalles plus larges. À l’inverse, un intervalle de prédiction plus faible (par exemple un intervalle de prédiction de 90 %) conduira à un intervalle plus étroit.
• Nous avons utilisé la formule =FORECAST() pour obtenir la valeur prédite pour ŷ ₀ mais la formule =FORECAST.LINEAR() renverra exactement la même valeur.