Comment effectuer un test de Kolmogorov-Smirnov dans Excel

Le test de Kolmogorov-Smirnov est utilisé pour déterminer si un échantillon est normalement distribué ou non.

Ce test est largement utilisé car de nombreux tests et procédures statistiques supposent que les données sont normalement distribuées.

L’exemple étape par étape suivant montre comment effectuer un test de Kolmogorov-Smirnov sur un exemple d’ensemble de données dans Excel.

Étape 1 : Saisissez les données

Commençons par saisir les valeurs d’un ensemble de données avec une taille d’échantillon de n = 20 :

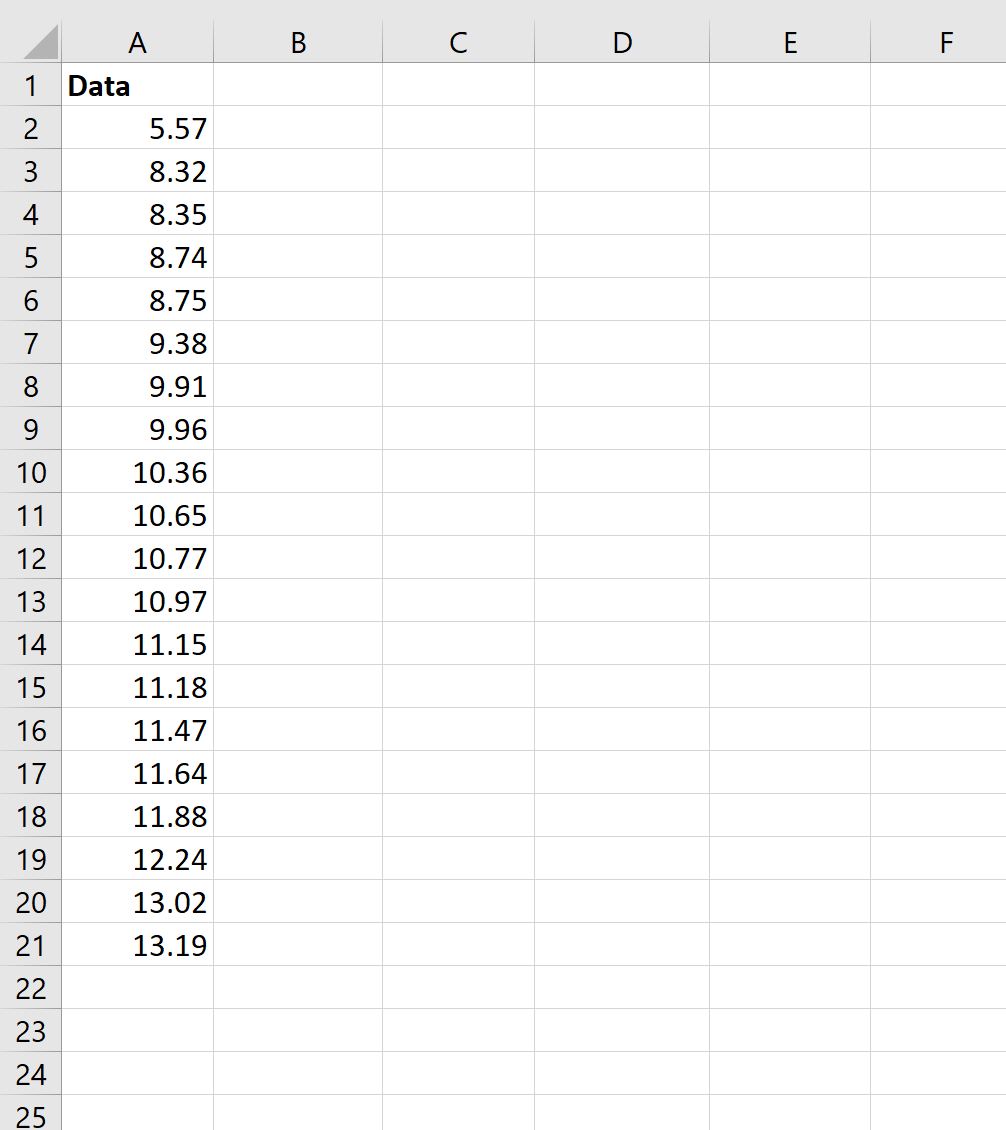
Étape 2 : Calculer les valeurs réelles et attendues à partir de la distribution normale

Ensuite, nous calculerons les valeurs réelles par rapport aux valeurs attendues de la distribution normale :

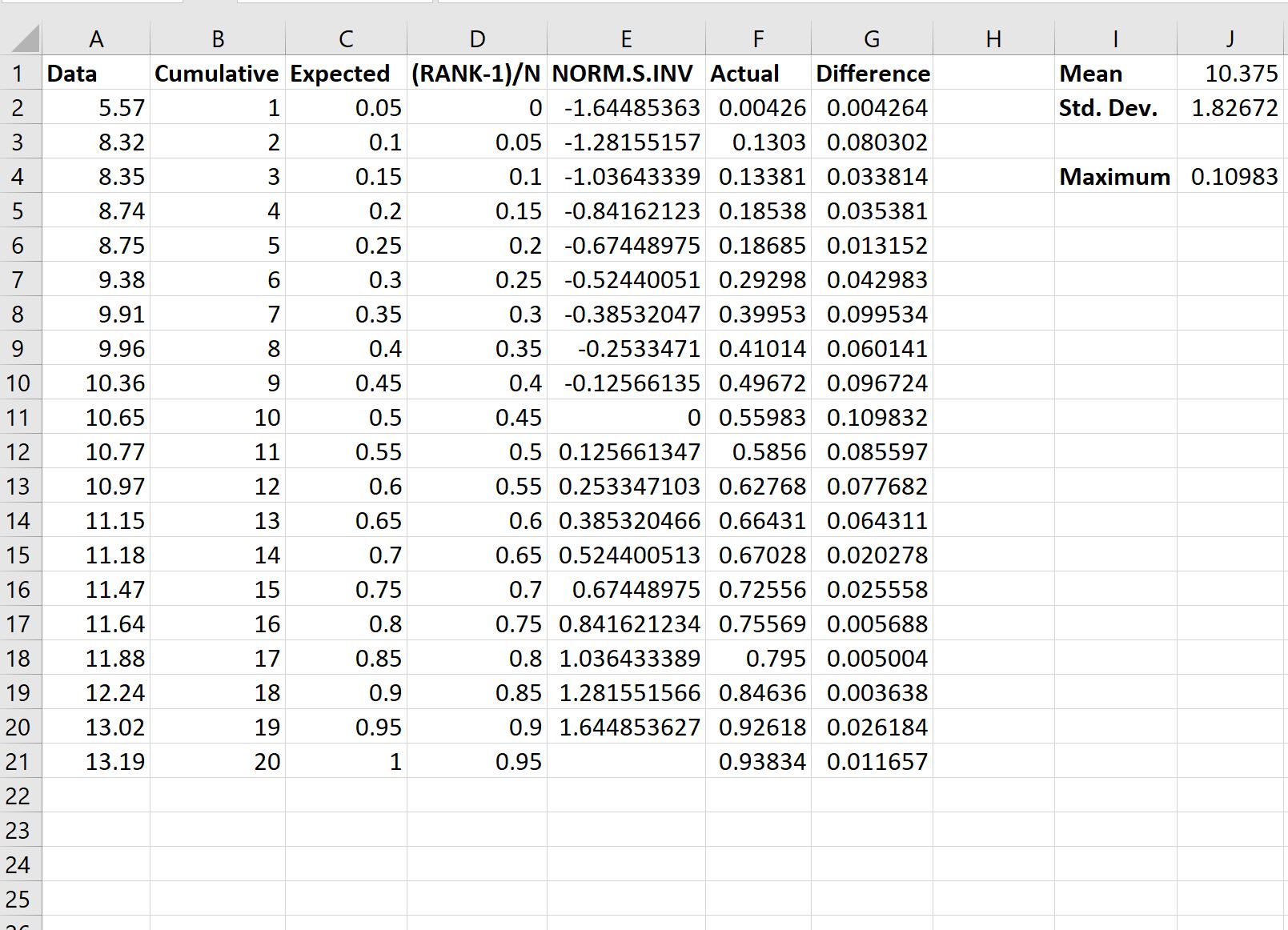
Voici la formule que nous avons utilisée dans différentes cellules :

• B2 : =LIGNE() – 1
• C2 : = B2 /COMPTE( $A$2:$A$21 )
• D2 : =( B2 -1)/COUNT( $A$2:$A$21 )
• E2 : =IF( C2 <1, NORM.S.INV( C2 ),””)
• F2 : =NORM.DIST( A2 , $J$1 , $J$2 , VRAI)
• G2 : =ABS( F2 – D2 )
• J1 : =MOYENNE( A2:A21 )
• J2 : =ETDEV.S( A2:A21 )
• J4 : =MAX( G2:G21 )

Étape 3 : Interpréter les résultats

Un test de Kolmogorov-Smirnov utilise les hypothèses nulles et alternatives suivantes :

• H ₀ : Les données sont normalement distribuées.
• H _A : Les données ne sont pas normalement distribuées.

Pour déterminer si nous devons rejeter ou non l’hypothèse nulle, nous devons nous référer à la valeur maximale dans la sortie, qui s’avère être 0,10983 .

Cela représente la différence absolue maximale entre les valeurs réelles de notre échantillon et les valeurs attendues d’une distribution normale.

Pour déterminer si cette valeur maximale est statistiquement significative, il faut se référer à un tableau de Kolmogorov-Smirnov des valeurs critiques et trouver le nombre égal à n = 20 et α = 0,05.

La valeur critique s’avère être de 0,190 .

Puisque notre valeur maximale n’est pas supérieure à cette valeur critique, nous ne parvenons pas à rejeter l’hypothèse nulle.

Cela signifie que nous pouvons supposer que nos exemples de données sont normalement distribués.

Ressources additionnelles

Les didacticiels suivants expliquent comment effectuer d’autres tests statistiques courants dans Excel :

Comment effectuer un test de corrélation dans Excel
Comment effectuer un test Durbin-Watson dans Excel
Comment effectuer un test Jarque-Bera dans Excel
Comment effectuer le test de Levene dans Excel