La causalité implique-t-elle une corrélation ? (3 exemples)
Il est bien connu que corrélation n’implique pas causalité .
À titre d’exemple simple, si nous collectons chaque année des données sur le nombre total de diplômés du secondaire et la consommation totale de pizza aux États-Unis, nous constaterions que les deux variables sont fortement corrélées :
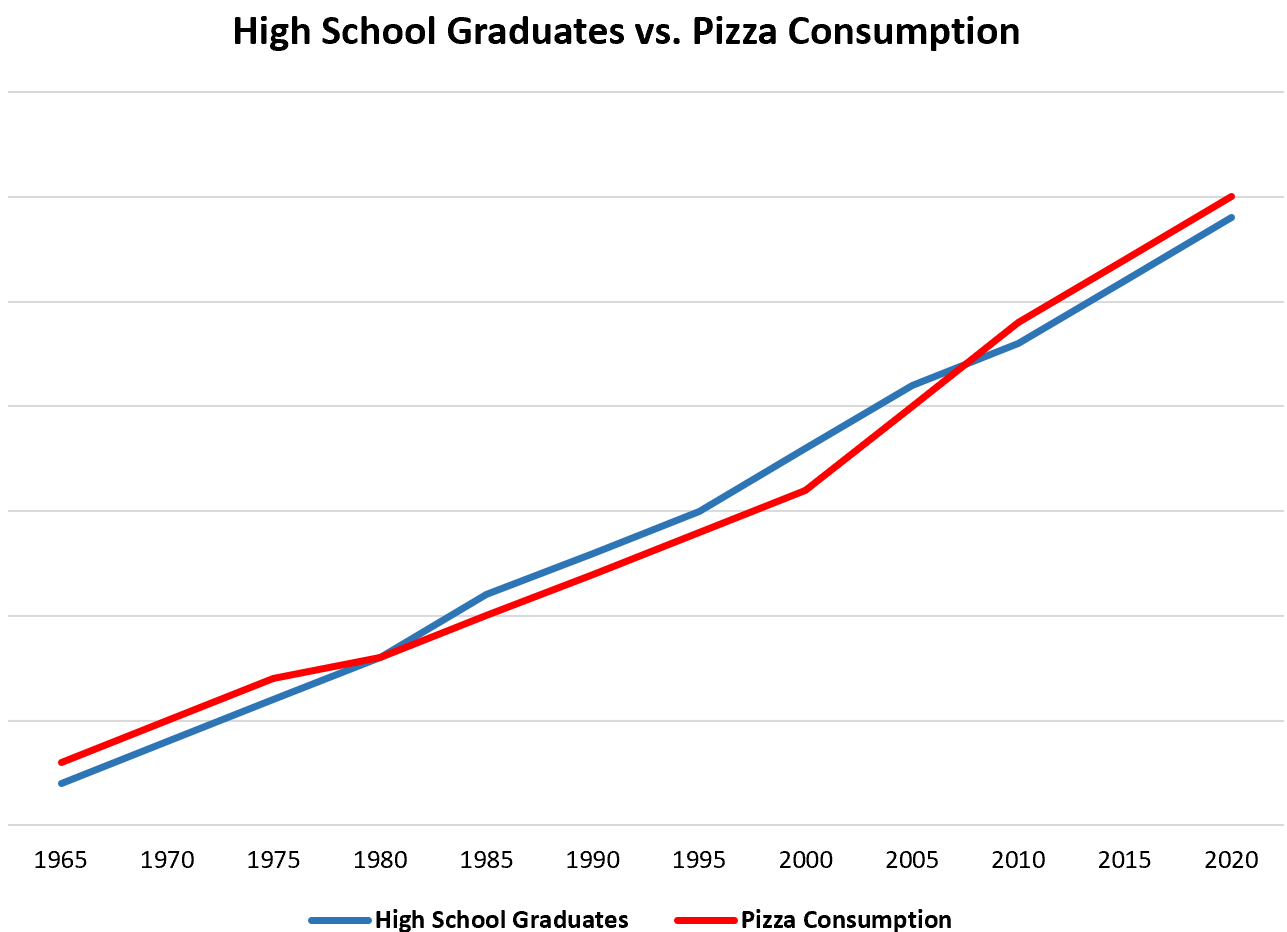
Cela ne signifie pas que l’augmentation du nombre de diplômés du secondaire entraîne une augmentation de la consommation de pizza.
L’explication la plus probable est que la population américaine a augmenté au fil du temps, ce qui signifie que le nombre de personnes titulaires d’un diplôme d’études secondaires et la quantité totale de pizza consommée augmentent à mesure que la population augmente.
Mais qu’en est-il de l’énoncé inverse : la causalité implique-t-elle une corrélation ?
Si une variable provoque une autre variable, cela signifie-t-il nécessairement que les deux variables seront corrélées ?
La réponse courte : Non .
Les exemples suivants montrent pourquoi.
Exemple 1 : relation quadratique
Supposons qu’une variable, X, fasse prendre à la variable Y une valeur égale à X 2 .
Par exemple:
- Si X = -10 alors Y = -10 2 = 100
- Si X = 0 alors Y = 0 2 = 0
- Si X = 10 alors Y = 10 2 = 100
Et ainsi de suite.
Si nous traçons la relation entre X et Y, cela ressemblerait à ceci :
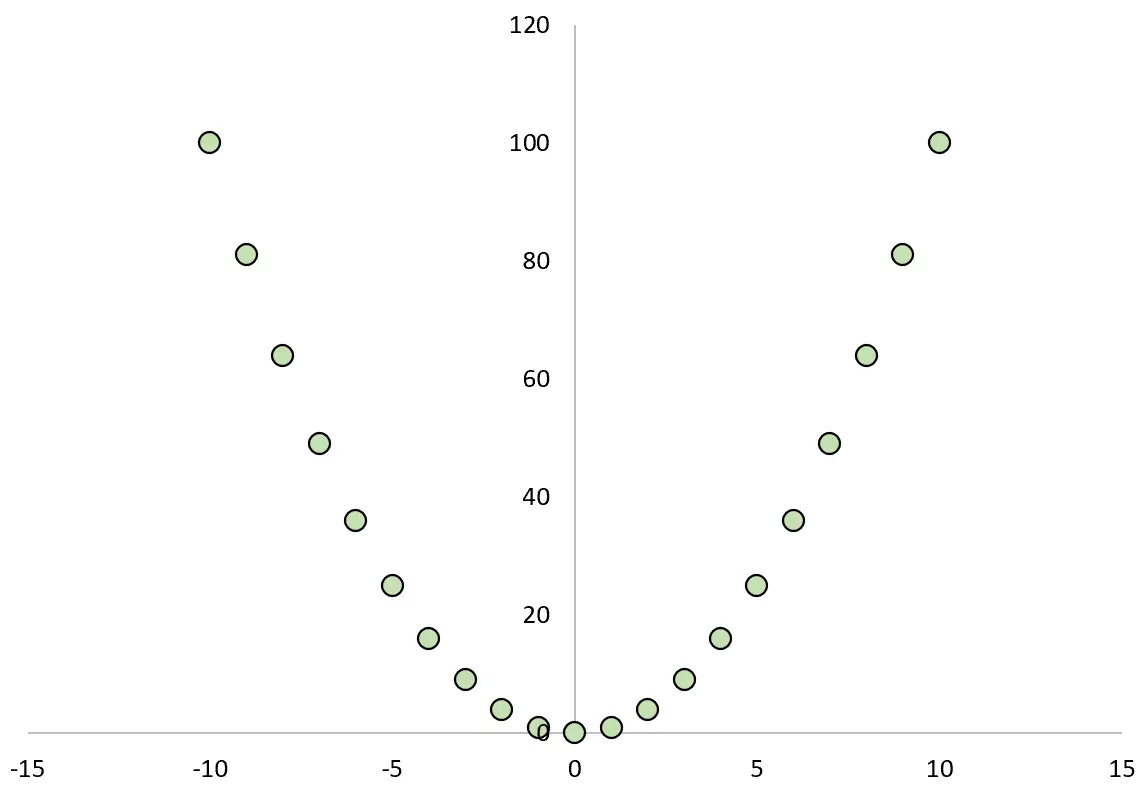
Si nous calculions le coefficient de corrélation de Pearson entre les deux variables, nous constaterions que la corrélation est nulle .
Bien que X provoque Y, la corrélation linéaire entre les deux variables est nulle.
Exemple 2 : relation quartique
Supposons qu’une variable, X, fasse prendre à la variable Y une valeur égale à X 4 .
Par exemple:
- Si X = -10 alors Y = -10 4 = 10 000
- Si X = 0 alors Y = 0 4 = 0
- Si X = 10 alors Y = 10 4 = 10 000
Et ainsi de suite.
Si nous traçons la relation entre X et Y, cela ressemblerait à ceci :
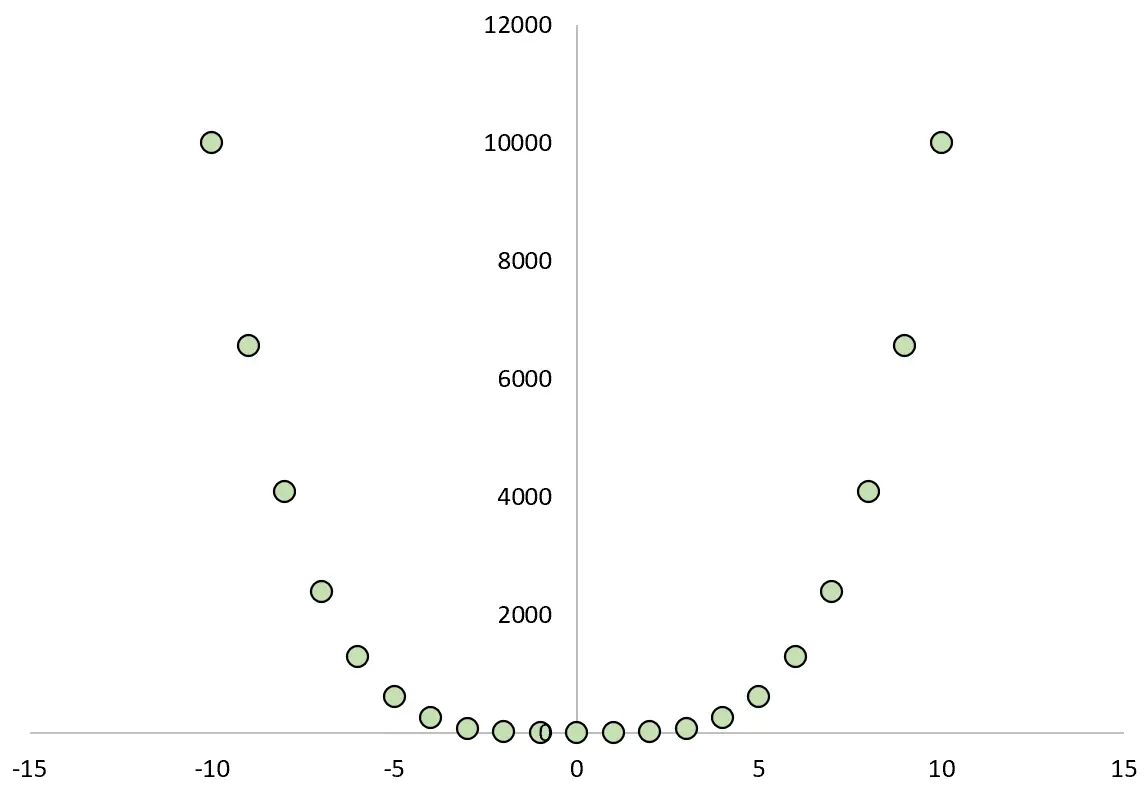
Si nous calculions le coefficient de corrélation de Pearson entre les deux variables, nous constaterions que la corrélation est nulle .
Nous savons que X provoque Y, mais la corrélation linéaire entre les deux variables est nulle.
Exemple 3 : relation cosinus
Supposons qu’une variable, X, fasse prendre à la variable Y une valeur égale à cos(X).
Par exemple:
- Si X = -10 alors Y = cos(-10) = -0,83907
- Si X = 0 alors Y = cos(0) = 1
- Si X = 10 alors Y = cos(10) = -0,83907
Et ainsi de suite.
Si nous traçons la relation entre X et Y, cela ressemblerait à ceci :
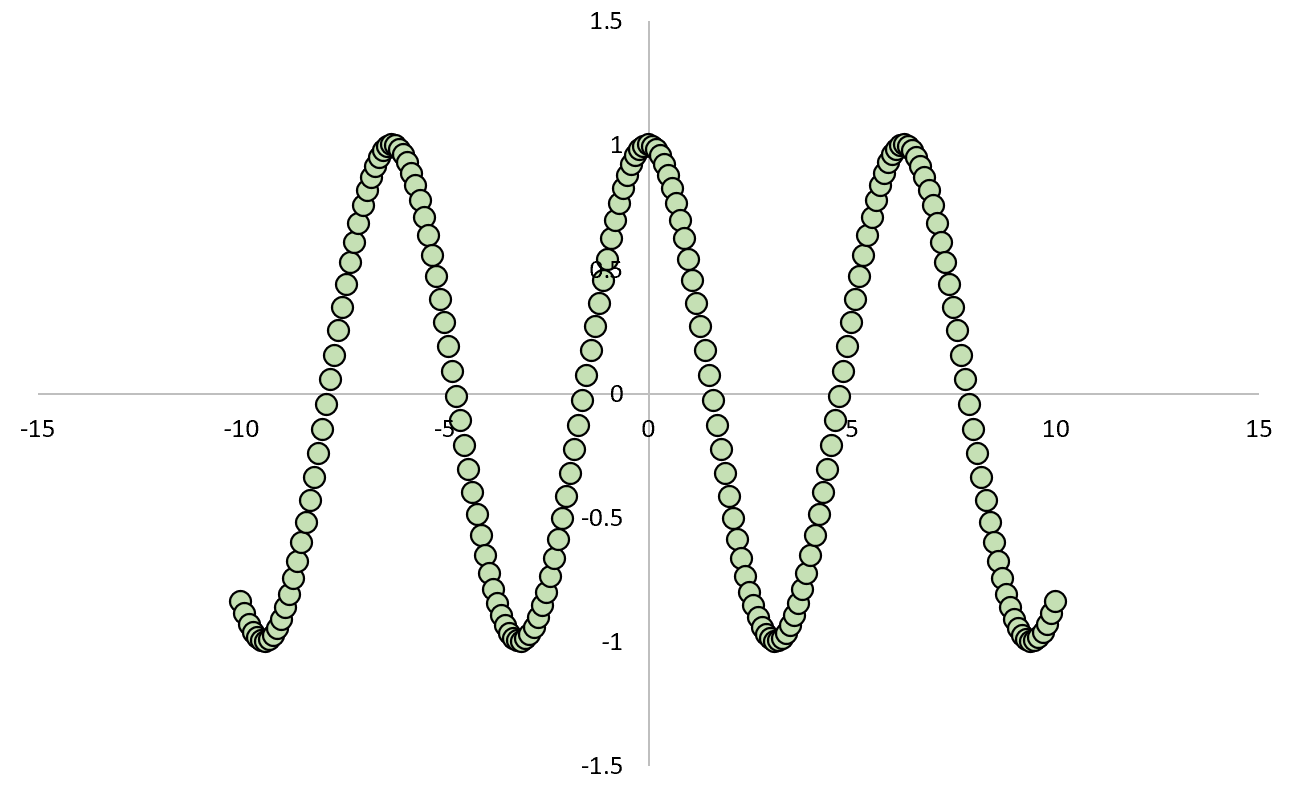
Si nous calculions le coefficient de corrélation de Pearson entre les deux variables, nous constaterions que la corrélation est nulle .
Nous savons que X provoque Y, mais la corrélation linéaire entre les deux variables est nulle.
Ressources additionnelles
Les didacticiels suivants fournissent des informations supplémentaires sur la corrélation et la causalité :
La corrélation n’implique pas la causalité : 5 exemples concrets
Introduction au coefficient de corrélation de Pearson
Causalité inverse : définition et exemples
