La distribution normale
La distribution normale est la distribution de probabilité la plus courante en statistique.
Les distributions normales ont les caractéristiques suivantes :
- Forme de cloche
- Symétrique
- La moyenne et la médiane sont égales ; les deux sont situés au centre de la distribution
- Environ 68 % des données se situent dans un écart type de la moyenne
- Environ 95 % des données se situent à moins de deux écarts types de la moyenne.
- Environ 99,7 % des données se situent dans une fourchette de trois écarts types par rapport à la moyenne.
Les trois derniers points sont connus sous le nom de règle empirique , parfois appelée règle 68-95-99,7 .
Connexes : Règle empirique (problèmes de pratique)
Comment dessiner une courbe normale
Pour tracer une courbe normale, nous devons connaître la moyenne et l’écart type.
Exemple 1 : Supposons que la taille des hommes dans une certaine école soit normalement distribuée avec une moyenne de un écart type de
Étape 1 : Esquissez une courbe normale.
Étape 2 : La moyenne de 70 pouces se situe au milieu.
Étape 3 : Chaque écart type correspond à une distance de 2 pouces.
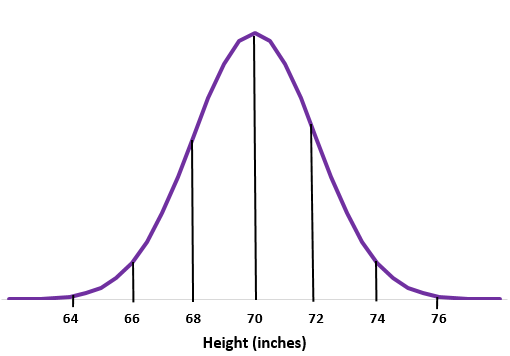
Exemple 2 : Supposons que le poids d’une certaine espèce de loutre soit normalement distribué avec une moyenne de un écart type de
Étape 1 : Esquissez une courbe normale.
Étape 2 : La moyenne de 30 livres se situe au milieu.
Étape 3 : Chaque écart type correspond à une distance de 5 lbs
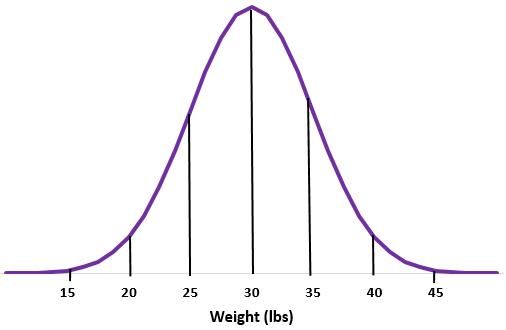
Comment trouver des pourcentages à l’aide de la distribution normale
La règle empirique , parfois appelée règle 68-95-99,7 , stipule que pour une variable aléatoire normalement distribuée, 68 % des données se situent dans une fourchette d’un écart type de la moyenne, 95 % se situent dans une fourchette de deux écarts types de la moyenne et 99,7 % se situent à moins de trois écarts types de la moyenne.
En utilisant cette règle, nous pouvons répondre à des questions sur les pourcentages.
Exemple : Supposons que la taille des hommes dans une certaine école soit normalement distribuée avec une moyenne de un écart type de
Solution:
Étape 1 : Esquissez une distribution normale avec une moyenne de un écart type de
Étape 2 : Une hauteur de 74 pouces correspond à deux écarts types au-dessus de la moyenne. Ajoutez les pourcentages au-dessus de ce point dans la distribution normale.
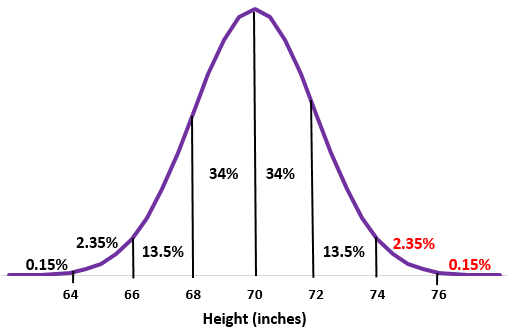
2,35% + 0,15% = 2,5%
Environ 2,5 % des hommes de cette école mesurent plus de 74 pouces.
Solution:
Étape 1 : Esquissez une distribution normale avec une moyenne de un écart type de
Étape 2 : Une hauteur de 68 pouces et 72 pouces correspond respectivement à un écart type en dessous et au-dessus de la moyenne. Ajoutez simplement les pourcentages entre ces deux points dans la distribution normale.
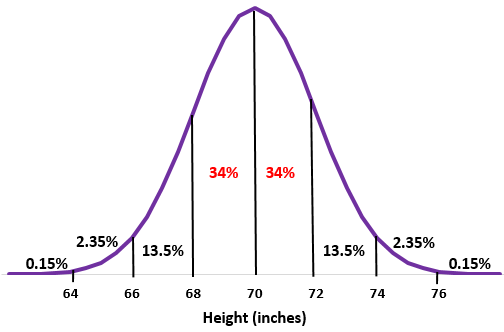
34% + 34% = 68%
Environ 68 % des hommes de cette école mesurent entre 68 pouces et 72 pouces.
Comment trouver des décomptes à l’aide de la distribution normale
Nous pouvons également utiliser la règle empirique pour répondre à des questions sur les décomptes.
Exemple : Supposons que le poids d’une certaine espèce de loutre soit normalement distribué avec une moyenne de un écart type de
Une certaine colonie compte 200 de ces loutres. Environ combien de ces loutres pèsent plus de 35 livres ?
Solution:
Étape 1 : Esquissez une distribution normale avec une moyenne de un écart type de
Étape 2 : Un poids de 35 lb correspond à un écart type au-dessus de la moyenne. Ajoutez les pourcentages au-dessus de ce point dans la distribution normale.
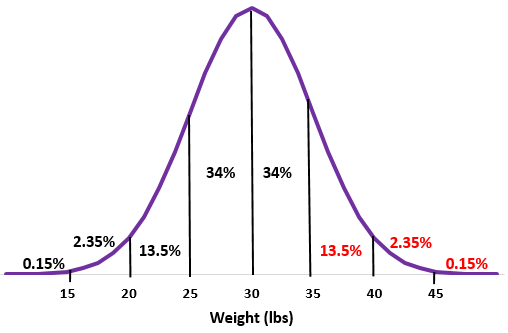
13,5% + 2,35% + 0,15% = 16%
Étape 3 : Puisqu’il y a 200 loutres dans la colonie, 16 % de 200 = 0,16 * 200 = 32
Environ 32 loutres de cette colonie pèsent plus de 35 livres.
Environ combien de loutres de cette colonie pèsent moins de 30 livres ?
Au lieu de suivre toutes les étapes que nous venons de suivre ci-dessus, nous pouvons reconnaître que la médiane d’une distribution normale est égale à la moyenne, qui est de 30 livres dans ce cas.
Cela signifie que la moitié des loutres pèsent plus de 30 livres et l’autre moitié moins de 30 livres. Cela signifie que 50 % des 200 loutres pèsent moins de 30 livres, donc 0,5 * 200 = 100 loutres .
Ressources additionnelles
Les didacticiels suivants offrent des informations supplémentaires sur la distribution normale :
6 exemples concrets de la distribution normale
Distribution normale vs distribution t : la différence
Comment créer une courbe en cloche dans Excel
Comment créer une courbe en cloche en Python
à propos de l'auteur
Dr. Benjamin Anderson
Il est un professeur de statistiques à la retraite devenu éducateur dévoué sur Statorials. Avec une vaste expérience et une expertise dans le domaine des statistiques, je m'engage à partager mes connaissances pour responsabiliser les étudiants grâce à Statorials. Lire plus