Limites de contrôle

Par Pr Amélia Rodriguez août 2, 2023 Gestion de la qualité 0 commentaire

Cet article explique ce qu’est une limite de contrôle et quelles sont les différentes limites de contrôle d’une carte de contrôle. Vous verrez également comment les limites de contrôle sont calculées ainsi qu’un exemple concret dans lequel les limites de contrôle d’un processus sont déterminées.

Que sont les limites de contrôle ?

Les limites de contrôle sont les lignes horizontales sur une carte de contrôle qui sont utilisées pour déterminer si un processus est contrôlé ou non.

Une carte de contrôle comporte deux limites de contrôle : les limites de contrôle supérieure et inférieure, qui délimitent respectivement la zone de contrôle au-dessus et en dessous.

Ainsi, les limites de contrôle sont des valeurs utilisées pour indiquer la zone de contrôle d’un processus. Si la mesure obtenue à partir d’un processus se situe dans les limites de contrôle, cela signifie que le processus est contrôlé. Dans le cas contraire, la machine ou le processus doit être vérifié car il est probable qu’il ait dévié.

Types de limites de contrôle

Les limites de contrôle sont :

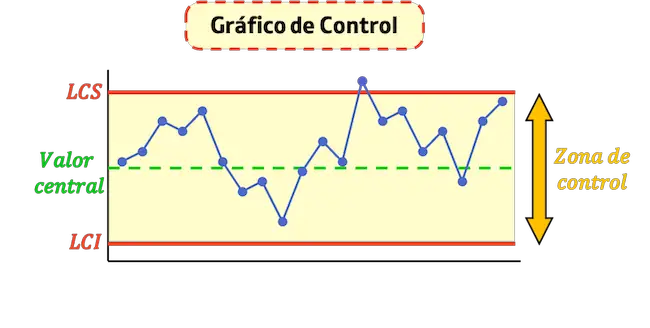
Limite supérieure de contrôle (LCS) : c’est la ligne qui indique la valeur maximale acceptée dans le processus.
Limite inférieure de contrôle (LCI) : c’est la ligne qui indique la valeur minimale acceptée dans le processus.
Ligne de contrôle centrale : C’est la ligne qui représente la valeur moyenne du graphique. Plus les points sont proches de cette ligne, plus le processus est stable.

Comment calculer les limites de contrôle

Actuellement, les limites de contrôle d’un processus sont généralement calculées par un logiciel informatique qui permet de contrôler le processus. Cependant, il est également important que vous sachiez comment elles sont calculées, car vous devrez peut-être les trouver manuellement.

Le calcul des limites de contrôle d’une carte de contrôle dépend du type de carte que vous souhaitez réaliser, puisque les valeurs changeront selon qu’il s’agit d’une carte de contrôle pour la moyenne ou pour l’étendue.

La carte de contrôle de la moyenne est un graphique dans lequel est évaluée l’évolution de la moyenne d’un processus. Ainsi, la moyenne d’un ensemble de valeurs est calculée à l’aide de la formule suivante :

$\overline{X}=\cfrac{\displaystyle \sum_{i=1}^n x_i}{n}$

Où:

$x_i$ est le numéro de mesure i.
$n$ est le nombre de mesures effectuées.

Nous désignerons la valeur centrale de la carte de contrôle pour la moyenne par

$\overline{\overline{X}}$ , qui est la moyenne des échantillons et est calculée avec l’expression suivante :

$\overline{\overline{X}}=\cfrac{\displaystyle \sum_{j=1}^m {\overline{X}_j}}{m}$

Où:

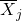$\overline{X}_j$ est la moyenne de l’échantillon j.
$m$ est le nombre d’échantillons prélevés.

➤ Voir : Calcul de la moyenne arithmétique

En revanche, la valeur centrale de la carte de contrôle de l’étendue est la moyenne des étendues de tous les échantillons prélevés :

$\overline{R}=\cfrac{\displaystyle \sum_{j=1}^m R_j}{m}$

Où:

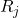$R_j$ est la plage de l’échantillon j.
$m$ est le nombre d’échantillons prélevés.

➤ Voir : Calcul de la plage statistique

Ainsi, les formules de calcul des limites de contrôle d’une carte de contrôle sont les suivantes :

carte de contrôle X

$\begin{array}{c}LCS=\overline{\overline{X}}+A_2\cdot \overline{R}\\[3ex]LCI=\overline{\overline{X}}-A_2\cdot \overline{R}\end{array}$

carte de contrôle R

$\begin{array}{c}LCS=D_4\cdot \overline{R}\\[3ex]LCI=D_3\cdot\overline{R}\end{array}$

Où les valeurs des paramètres A ₂ , D ₃ et D ₄ se retrouvent dans le tableau suivant :

Taille (n°)	À ₂	J ₃	_J4
2	1 880	0,000	3 267
3	1 023	0,000	2 575
4	0,729	0,000	2 282
5	0,577	0,000	2 115
6	0,483	0,000	2 004
7	0,419	0,076	1 924
8	0,373	0,136	1 864
9	0,337	0,184	1 816
dix	0,308	0,223	1 777

Exemple de calcul des limites de contrôle

Une entreprise industrielle souhaite contrôler la mesure du diamètre d’un cylindre pour voir si son processus de production est maîtrisé. Pour ce faire, prélevez un échantillon de 5 cylindres toutes les 15 minutes et mesurez leur diamètre. Le tableau suivant montre l’enregistrement des mesures.

Pour trouver les limites de contrôle, nous devons d’abord prendre la moyenne arithmétique et la plage de chaque ensemble de mesures :

exemples de calculs de carte de contrôle

Calculons maintenant la moyenne des moyennes et des plages, qui seront respectivement les valeurs centrales de la carte de contrôle pour la moyenne et pour la plage :

$\overline{\overline{X}}=\cfrac{\displaystyle \sum_{j=1}^m {\overline{X}_j}}{m}=4,8589$

$\overline{R}=\cfrac{\displaystyle \sum_{j=1}^m R_j}{m}=0,0227$

Dans ce cas, chaque échantillon est composé de 5 mesures, les coefficients des formules de limite de contrôle sont donc les suivants :

$A_2=0,577$

$D_3=0$

$D_4=2,115$

Nous calculons les limites de contrôle supérieure et inférieure de la carte de contrôle moyenne et étendue :

Limites de contrôle de la carte de contrôle

$\begin{array}{c}LCS=\overline{\overline{X}}+A_2\cdot \overline{R}=4,8589+0,577\cdot 0,0227=4,8720\\[3ex]LCI=\overline{\overline{X}}-A_2\cdot \overline{R}=4,8589-0,577\cdot 0,0227=4,8458\end{array}$

Limites de contrôle de Carte de contrôle R

$\begin{array}{c}LCS=D_4\cdot \overline{R}=2,115\cdot 0,0227=0,0481\\[3ex]LCI=D_3\cdot\overline{R}=0\cdot 0,0227=0\end{array}$

Les cartes de contrôle de l’exercice sont donc les suivantes :

exemple de calcul des limites de contrôle

Dans la première carte de contrôle, nous pouvons voir que deux valeurs sont inférieures à la limite de contrôle inférieure. De plus, dans la deuxième carte de contrôle, il y a également une valeur au-dessus de la limite de contrôle supérieure. Le processus n’est donc pas contrôlé.

à propos de l'auteur

Pr Amélia Rodriguez

En mettant l'accent sur l'apprentissage interactif et les applications pratiques, la professeure Amélia Rodriguez propose des tutoriels complets et des exemples concrets pour rendre les concepts de probabilité accessibles et pertinents pour la vie de ses étudiants. Lire plus