Loi de probabilité totale : définition & Exemples

Dans la théorie des probabilités, la loi de la probabilité totale est un moyen utile de trouver la probabilité d’un événement A lorsque nous ne connaissons pas directement la probabilité de A mais que nous savons que les événements B ₁ , B ₂ , B ₃ … forment une partition. de l’ espace échantillon S .

Cette loi précise ce qui suit :

La loi de la probabilité totale

Si B ₁ , B ₂ , B ₃ … forment une partition de l’espace échantillon S , alors nous pouvons calculer la probabilité de l’événement A comme suit :

P( UNE ) = ΣP( UNE | B _je )*P( B _je )

La façon la plus simple de comprendre cette loi est de prendre un exemple simple.

Supposons qu’il y ait deux sacs dans une boîte contenant les billes suivantes :

• Sac 1 : 7 billes rouges et 3 billes vertes
• Sac 2 : 2 billes rouges et 8 billes vertes

Si nous sélectionnons au hasard l’un des sacs, puis sélectionnons au hasard une bille de ce sac, quelle est la probabilité que ce soit une bille verte ?

Dans cet exemple, soit P( G ) = probabilité de choisir une bille verte. C’est la probabilité qui nous intéresse, mais nous ne pouvons pas la calculer directement.

Au lieu de cela, nous devons utiliser la probabilité conditionnelle de G , étant donné certains événements B où les B _i forment une partition de l’espace échantillon S . Dans cet exemple, nous avons les probabilités conditionnelles suivantes :

• P(G| _B1 ) = 3/10 = 0,3
• P(G| _B2 ) = 8/10 = 0,8

Ainsi, en utilisant la loi de la probabilité totale, nous pouvons calculer la probabilité de choisir une bille verte comme suit :

• P(G) = ΣP(G|B _je )*P(B _je )
• P(G) = P(G|B ₁ )*P(B ₁ ) + P(G|B ₂ )*P(B ₂ )
• P(G) = (0,3)*(0,5) + (0,8)*(0,5)
• P(G) = 0,55

Si nous sélectionnons au hasard l’un des sacs, puis sélectionnons au hasard une bille de ce sac, la probabilité que nous choisissions une bille verte est de 0,55 .

Lisez les deux exemples suivants pour consolider votre compréhension de la loi de la probabilité totale.

Exemple 1 : Widgets

L’entreprise A fournit 80 % des widgets à un atelier automobile et seulement 1 % de ses widgets s’avèrent défectueux. La société B fournit les 20 % de widgets restants au garage automobile et 3 % de ses widgets s’avèrent défectueux.

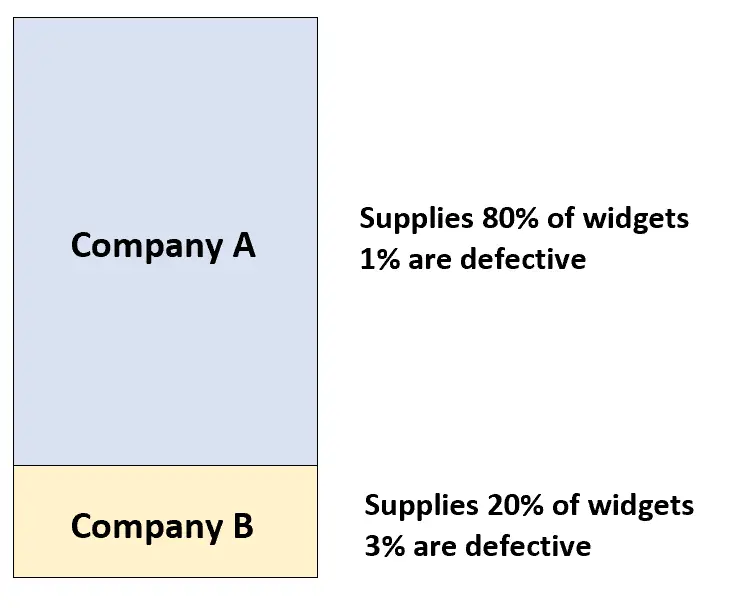
Si un client achète au hasard un widget dans un garage automobile, quelle est la probabilité qu’il soit défectueux ?

Si nous laissons P( D ) = la probabilité qu’un widget soit défectueux et P(B _i ) la probabilité que le widget provienne de l’une des sociétés, alors nous pouvons calculer la probabilité d’acheter un widget défectueux comme suit :

• P(D) = ΣP(D|B _je )*P(B _je )
• P(D) = P(D|B ₁ )*P(B ₁ ) + P(D|B ₂ )*P(B ₂ )
• P(D) = (0,01)*(0,80) + (0,03)*(0,20)
• P(D) = 0,014

Si nous achetons au hasard un widget dans ce magasin automobile, la probabilité qu’il soit défectueux est de 0,014 .

Exemple 2 : Forêts

La forêt A occupe 50 % de la superficie totale d’un certain parc et 20 % des plantes de cette forêt sont vénéneuses. La forêt B occupe 30 % de la superficie totale et 40 % des plantes qu’elle contient sont vénéneuses. La forêt C occupe les 20 % restants du territoire et 70 % des plantes qui s’y trouvent sont vénéneuses.

Si nous entrons au hasard dans ce parc et cueillons une plante sur le sol, quelle est la probabilité qu’elle soit toxique ?

Si nous laissons P( P ) = la probabilité que la plante soit toxique, et P(B _i ) la probabilité que nous soyons entrés dans l’une des trois forêts, alors nous pouvons calculer la probabilité qu’une plante choisie au hasard soit toxique comme :

• P(P) = ΣP(P|B _je )*P(B _je )
• P(P) = P(P|B ₁ )*P(B ₁ ) + P(P|B ₂ )*P(B ₂ ) + P(P|B ₃ )*P(B ₃ )
• P(P) = (0,20)*(0,50) + (0,40)*(0,30) + (0,70)*(0,20)
• P(P) = 0,36

Si l’on choisit au hasard une plante sur le sol, la probabilité qu’elle soit toxique est de 0,36 .

Ressources additionnelles

Les didacticiels suivants fournissent des informations supplémentaires sur des sujets liés aux probabilités :

Comment trouver la moyenne d’une distribution de probabilité
Comment trouver l’écart type d’une distribution de probabilité
Calculateur de distribution de probabilité