Distribution de Pareto
Cet article explique ce qu’est la distribution de Pareto dans les statistiques et à quoi elle sert. Vous pourrez également voir le graphique de la distribution de Pareto et les propriétés de ce type de distribution de probabilité.
Qu’est-ce que la distribution de Pareto ?
La distribution de Pareto est une distribution de probabilité continue utilisée en statistique pour modéliser le principe de Pareto. Par conséquent, la distribution de Pareto est une distribution de probabilité qui a quelques valeurs dont la probabilité d’occurrence est bien supérieure au reste des valeurs.
Rappelons que la loi de Pareto, également appelée règle des 80-20, est un principe statistique qui dit que l’essentiel de la cause d’un phénomène est dû à une petite partie de la population.
La distribution de Pareto a deux paramètres caractéristiques : le paramètre d’échelle x m et le paramètre de forme α.
À l’origine, la distribution de Pareto était utilisée pour décrire la répartition de la richesse au sein de la population, car la majeure partie de celle-ci était due à une petite proportion de la population. Mais actuellement, la distribution de Pareto a de nombreuses applications, par exemple dans le contrôle qualité, en économie, en science, dans le domaine social, etc.
La distribution de Pareto doit son nom à l’économiste Vilfredo Pareto, qui a formulé la distribution. Cependant, il est surtout connu pour le diagramme de Pareto.
Tableau de distribution de Pareto
Maintenant que nous connaissons la définition de la distribution de Pareto, regardons plusieurs exemples de distributions de Pareto représentées graphiquement.
Ainsi, ci-dessous vous pouvez voir à quoi ressemble le graphique de la fonction de densité de la distribution de Pareto en fonction de ses valeurs caractéristiques :
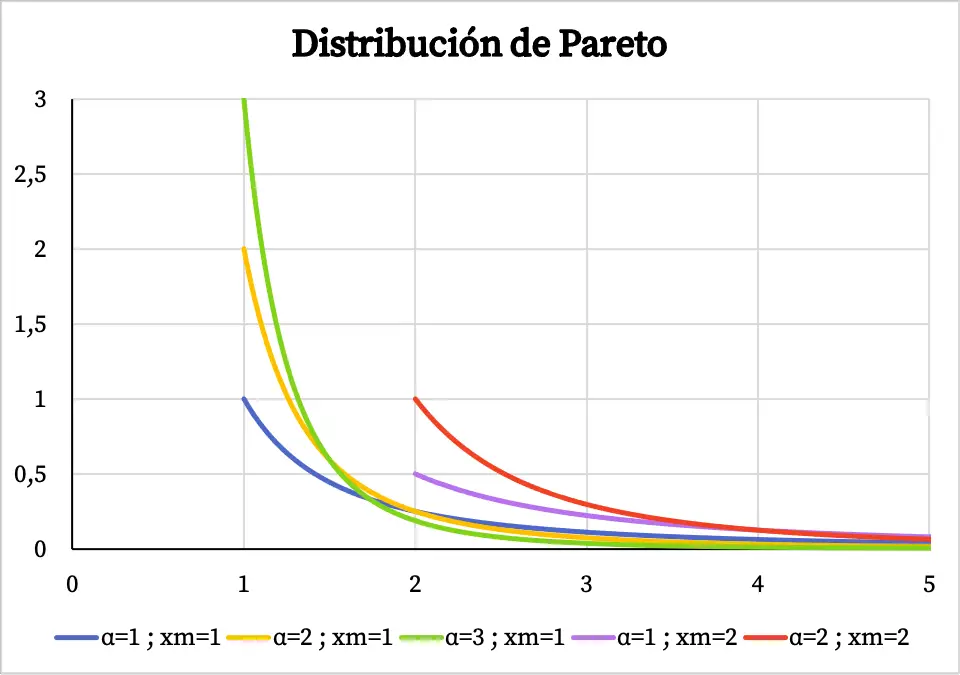
Notez que le domaine de la distribution de Pareto va de la valeur x m à +∞, c’est pourquoi la fonction de densité n’existe pas avant la valeur de x m .
D’autre part, le graphique de la fonction de probabilité cumulée de la distribution de Pareto est le suivant :
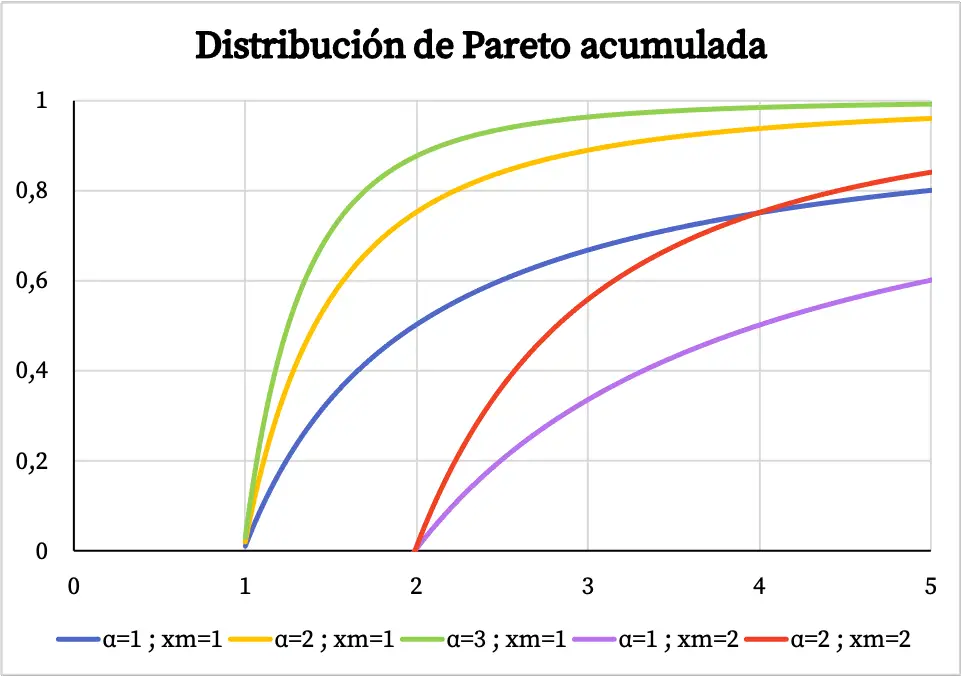
Caractéristiques de la distribution de Pareto
Vous trouverez ci-dessous les caractéristiques les plus importantes de la distribution de Pareto liées à la théorie des probabilités et aux statistiques.
- La distribution de Pareto possède deux paramètres caractéristiques qui définissent sa courbe : le paramètre d’échelle x m et le paramètre de forme α.
- Le domaine de la distribution de Pareto est constitué de tous les nombres réels depuis le paramètre d’échelle jusqu’à plus l’infini.
- Si α est supérieur à 1, la moyenne de la distribution de Pareto est égale au produit de α fois x m sur α moins 1.
![E[X]=\cfrac{\alpha\cdot x_m}{\alpha-1}\quad\text{para } \alpha>1](https://statorials.org/wp-content/ql-cache/quicklatex.com-6d26513868f9ed6fa45ab0fde0030884_l3.png "Rendered by QuickLaTeX.com")
- La variance de la distribution de Pareto dépend des deux paramètres caractéristiques de la distribution et se calcule avec la formule suivante :
- La médiane de la distribution de Pareto peut être déterminée avec l’expression suivante :
![\displaystyle Me=x_\mathrm{m}\cdot \sqrt[\alpha]{2}](https://statorials.org/wp-content/ql-cache/quicklatex.com-0dc2c772a0a0662ad05f8b22c3cf1ba1_l3.png "Rendered by QuickLaTeX.com")
- Le mode de la distribution Pareto est équivalent au paramètre d’échelle x m de la distribution.
- La formule de la fonction de densité de la distribution de Pareto est la suivante :
![\displaystyle P[X=x]=\frac{\alpha\cdot x_m^\alpha}{x^{\alpha+1}}\quad\text{para }x\geq x_m](https://statorials.org/wp-content/ql-cache/quicklatex.com-1e182771cfe3bf9a145a2ee59b9c7eeb_l3.png "Rendered by QuickLaTeX.com")
- De même, la formule de la fonction de probabilité cumulative de la distribution de Pareto est la suivante :
![\displaystyle P[X\leq x]=1-\left(\frac{x_\mathrm{m}}{x}\right)^\alpha](https://statorials.org/wp-content/ql-cache/quicklatex.com-480adc7841b7c72cb4bfecb446ed3fab_l3.png "Rendered by QuickLaTeX.com")
- Le coefficient d’asymétrie de la distribution de Pareto dépend uniquement du paramètre de forme α et son expression est :
- Le coefficient d’aplatissement de la distribution de Pareto varie également en fonction de la valeur du paramètre α et est calculé à l’aide de la formule suivante :
à propos de l'auteur
Pr Amélia Rodriguez
En mettant l'accent sur l'apprentissage interactif et les applications pratiques, la professeure Amélia Rodriguez propose des tutoriels complets et des exemples concrets pour rendre les concepts de probabilité accessibles et pertinents pour la vie de ses étudiants. Lire plus