Test de Brown – Forsythe dans R : exemple étape par étape
Une ANOVA unidirectionnelle est utilisée pour déterminer s’il existe ou non une différence significative entre les moyennes de trois groupes indépendants ou plus.
L’une des hypothèses d’une ANOVA unidirectionnelle est que les variances des populations dont proviennent les échantillons sont égales.
L’un des moyens les plus courants de tester cela consiste à utiliser un test de Brown-Forsythe , qui est un test statistique qui utilise les hypothèses suivantes :
- H 0 : Les variances entre les populations sont égales.
- H A : Les écarts entre les populations ne sont pas égaux.
Si la valeur p du test est inférieure à un certain niveau de signification (par exemple α = 0,05), alors nous rejetons l’hypothèse nulle et concluons que les variances ne sont pas égales entre les différentes populations.
Ce didacticiel fournit un exemple étape par étape de la façon d’effectuer un test de Brown-Forsythe dans R.
Étape 1 : Saisissez les données
Supposons que nous aimerions savoir si trois programmes d’entraînement différents conduisent ou non à différents niveaux de perte de poids.
Pour tester cela, nous recrutons 90 personnes et en assignons 30 au hasard pour utiliser chaque programme. Nous mesurons ensuite la perte de poids de chaque personne au bout d’un mois.
L’ensemble de données suivant contient des informations sur la quantité de poids perdue avec chaque programme :
#make this example reproducible set.seed(0) #create data frame data <- data.frame(program = as.factor(rep(c("A", "B", "C"), each = 30)), weight_loss = c(runif(30, 0, 3), runif(30, 0, 5), runif(30, 1, 7))) #view first six rows of data frame head(data) # program weight_loss #1 A 2.6900916 #2 A 0.7965260 #3 A 1.1163717 #4 A 1.7185601 #5 A 2.7246234 #6 A 0.6050458
Étape 2 : Résumer et visualiser les données
Avant d’effectuer un test de Brown-Forsythe, nous pouvons créer des diagrammes en boîte pour visualiser la variance de la perte de poids pour chaque groupe :
boxplot(weight_loss ~ program, data = data)
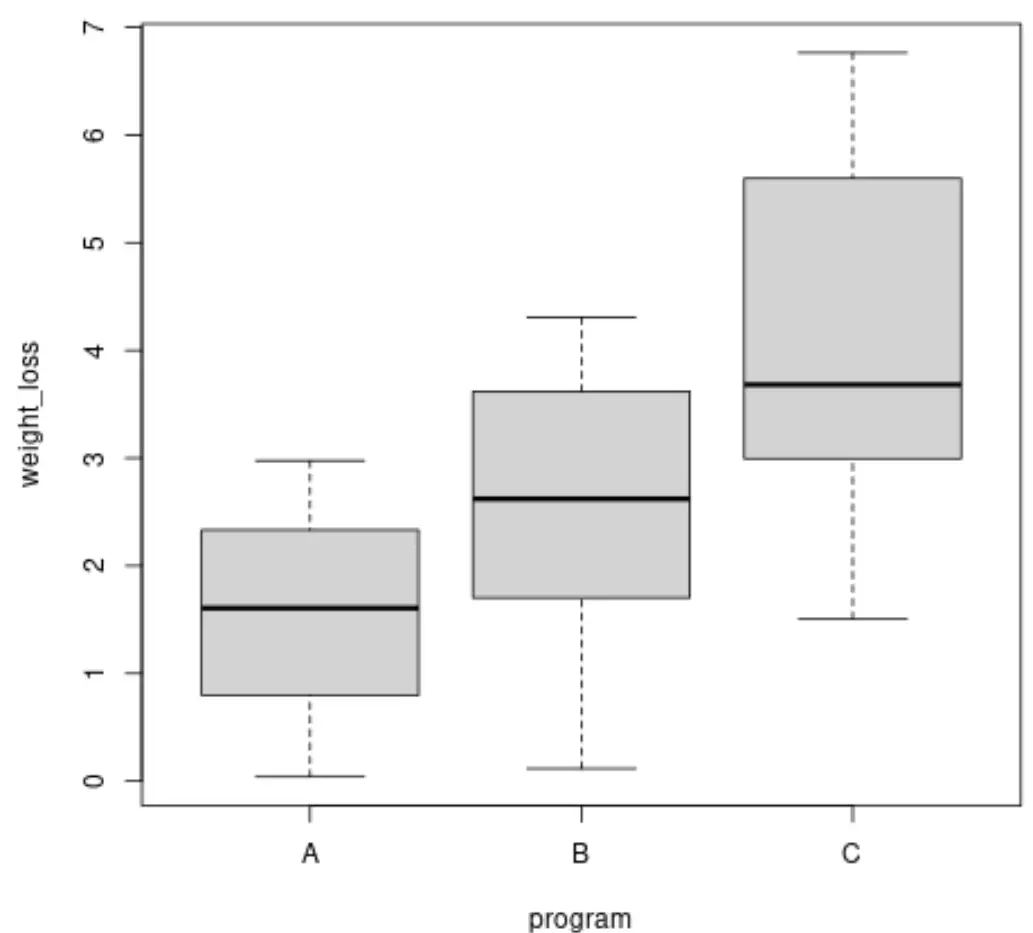
Nous pouvons également calculer la variance de la perte de poids dans chaque groupe :
#load dplyr package library(dplyr) #calculate variance of weight loss by group data %>% group_by(program) %>% summarize(var=var(weight_loss)) # A tibble: 3 x 2 program var 1 A 0.819 2 B 1.53 3 C 2.46
Nous pouvons voir que les variances entre les groupes diffèrent, mais pour déterminer si ces différences sontstatistiquement significatives , nous pouvons effectuer le test de Brown-Forsythe.
Étape 3 : Effectuer le test de Brown-Forsythe
Pour effectuer un test de Brown-Forsythe dans R, nous pouvons utiliser la fonction bf.test() du package onewaytests :
#load onewaytests package library(onewaytests) #perform Brown-Forsythe test bf.test(weight_loss ~ program, data = data) Brown-Forsythe Test (alpha = 0.05) ------------------------------------------------------------- data : weight_loss and program statistic : 30.83304 num df : 2 denom df : 74.0272 p.value : 1.816529e-10 Result : Difference is statistically significant. -------------------------------------------------------------
La valeur p du test s’avère inférieure à 0,000 et, comme l’indique le résultat, les différences de variances entre les trois groupes sont statistiquement significatives.
Prochaines étapes
Si vous ne parvenez pas à rejeter l’hypothèse nulle du test de Brown-Forsythe, vous pouvez alors procéder à une ANOVA unidirectionnelle sur les données.
Cependant, si vous rejetez l’hypothèse nulle, cela signifie que l’hypothèse d’égalité des variances est violée. Dans ce cas, vous avez deux options :
1. Procédez quand même à une ANOVA unidirectionnelle.
Il s’avère qu’une ANOVA unidirectionnelle est en fait robuste aux variances inégales tant que la plus grande variance n’est pas supérieure à 4 fois la plus petite variance.
À l’étape 2 de l’exemple ci-dessus, nous avons constaté que la plus petite variance était de 0,819 et la plus grande variance était de 2,46. Ainsi, le rapport de la variance la plus grande à la plus petite est 2,46 / 0,819 = 3,003 .
Puisque cette valeur est inférieure à 4, nous pourrions simplement procéder à l’ANOVA unidirectionnelle.
2. Effectuez un test de Kruskal-Wallis
Si le rapport de la plus grande variance à la plus petite variance est supérieur à 4, on peut plutôt choisir d’effectuer un test de Kruskal-Wallis . Ceci est considéré comme l’équivalent non paramétrique de l’ANOVA unidirectionnelle.
Vous pouvez trouver un exemple étape par étape d’un test de Kruskal-Wallis dans R ici .
