Matrice de corrélation

Par Pr Amélia Rodriguez août 5, 2023 Statistiques 0 commentaire

Dans cet article vous découvrirez ce qu’est une matrice de corrélation, quelle est sa formule et comment interpréter une matrice de corrélation. De plus, vous pourrez voir un exemple concret de l’interprétation d’une matrice de corrélation.

Qu’est-ce qu’une matrice de corrélation ?

La matrice de corrélation est une matrice qui contient en position i,j le coefficient de corrélation entre les variables i et j .

Par conséquent, la matrice de corrélation est une matrice carrée remplie de un sur la diagonale principale et l’élément de la ligne i et de la colonne j est constitué de la valeur du coefficient de corrélation entre la variable i et la variable j .

La formule de la matrice de corrélation est donc la suivante :

Où

$r_{ij}$ est le coefficient de corrélation entre les variables $i$ et $j.$

Ainsi, afin de trouver la matrice de corrélation d’un ensemble de données, il est essentiel que vous sachiez comment le coefficient de corrélation est calculé. Au cas où vous ne vous en souvenez pas, dans le lien suivant, vous découvrirez comment le faire avec une calculatrice en ligne :

➤ Voir : calculateur de coefficient de corrélation

Une propriété du coefficient de corrélation est que l’ordre des variables n’a pas d’importance pour son calcul, c’est-à-dire que le coefficient de corrélation

$r_{ij}$ est équivalent à $r_{ji}.$ Par conséquent, la matrice de corrélation est symétrique.

$\displaystyle R=\begin{pmatrix}1&r_{12}&r_{13}&\dots&r_{1n}\\[1.1ex] r_{12}&1&r_{23}&\dots&r_{2n}\\[1.1ex] r_{13}&r_{23}&1&\dots&r_{3n}\\[1.1ex] \vdots &\vdots &\vdots &\ddots &\vdots\\[1.1ex] r_{1n}&r_{2n}&r_{3n}&\dots&1\end{pmatrix}$

Pour qu’une matrice de corrélation ait un sens, l’ensemble de données statistiques doit comporter plus de deux variables. Autrement, il suffirait de déterminer un seul coefficient de corrélation et la matrice de corrélation n’aurait aucun sens.

Comment faire une matrice de corrélation

Compte tenu de la définition de la matrice de corrélation, voyons comment est réalisé ce type de matrice statistique :

Calculez le coefficient de corrélation de chaque paire de variables. Notez que l’ordre des variables ne change pas le résultat, il ne doit donc être calculé qu’une seule fois pour chaque paire de variables.
Créez une matrice carrée de la même dimension que le nombre de variables dans la série de données. Cette matrice sera la matrice de corrélation.
Mettez un 1 dans chaque élément de la diagonale principale de la matrice de corrélation.
Mettez le coefficient de corrélation des variables i , j dans les positions i , j et j , i .
Une fois la matrice de corrélation réalisée, il ne reste plus qu’à interpréter ses valeurs.

Gardez à l’esprit que simplement exécuter la matrice de corrélation ne suffit pas, vous devez ensuite interpréter ses valeurs et comprendre ce qu’elles signifient. La section suivante explique comment interpréter une matrice de corrélation.

Interprétation de la matrice de corrélation

Pour interpréter correctement la matrice de corrélation, il faut tenir compte du fait que la valeur du coefficient de corrélation peut aller de -1 à +1 :

r=-1 : les deux variables ont une corrélation négative parfaite, on peut donc tracer une ligne avec une pente négative dans laquelle se trouvent tous les points.
-1<r<0 : la corrélation entre les deux variables est négative, donc lorsqu’une variable augmente l’autre diminue. Plus la valeur est proche de -1, plus les variables sont liées négativement.
r=0 : la corrélation entre les deux variables est très faible, en effet, la relation linéaire entre elles est nulle. Cela ne signifie pas que les variables sont indépendantes, car elles pourraient avoir une relation non linéaire.
0<r<1 : la corrélation entre les deux variables est positive, plus la valeur est proche de +1, plus la relation entre les variables est forte. Dans ce cas, une variable a tendance à augmenter sa valeur lorsque l’autre augmente également.
r=1 : les deux variables ont une corrélation positive parfaite, c’est-à-dire qu’elles ont une relation linéaire positive.

Ainsi, pour interpréter la matrice de corrélation, il faut faire une interprétation de chaque coefficient de corrélation et comparer les différents résultats.

De cette façon, vous pourrez voir quelles variables sont les plus liées les unes aux autres, quelles variables sont les plus importantes, quelles variables n’ont pratiquement aucune relation les unes avec les autres, etc.

Exemple de matrice de corrélation

Pour bien comprendre en quoi consiste la matrice de corrélation et comment elle est interprétée, dans cette section nous analyserons un exemple de matrice de corrélation :

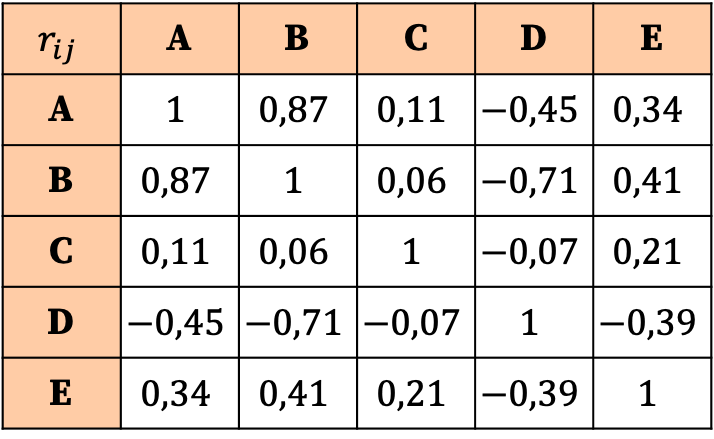
L’interprétation de la matrice de corrélation repose sur les valeurs des coefficients. Ainsi, on peut voir que la corrélation la plus forte est la relation entre la variable A et la variable B, puisque son coefficient correspondant est le plus grand (0,87).

En revanche, la variable C n’a pratiquement aucune corrélation avec aucune variable, puisque tous ses coefficients sont très proches de zéro et donc très faibles. Ainsi, pour simplifier l’analyse, on pourrait même envisager de supprimer cette variable de l’étude statistique.

De même, toutes les relations de la variable D avec les autres variables sont négatives, ce qui signifie que la corrélation entre la variable D et les autres variables est inverse. Cela n’implique pas que la variable doit être éliminée, mais simplement que la variable D est corrélée négativement.

Comme vous pouvez le constater, la matrice de corrélation est très utile pour résumer les données et faire une analyse globale de la relation entre les différentes variables de l’ensemble de données.

à propos de l'auteur

Pr Amélia Rodriguez

En mettant l'accent sur l'apprentissage interactif et les applications pratiques, la professeure Amélia Rodriguez propose des tutoriels complets et des exemples concrets pour rendre les concepts de probabilité accessibles et pertinents pour la vie de ses étudiants. Lire plus