Comment créer une matrice de corrélation dans R (4 exemples)

Une matrice de corrélation est un tableau carré qui montre les coefficients de corrélation entre les variables d’un ensemble de données.

Il offre un moyen rapide de comprendre la force des relations linéaires qui existent entre les variables d’un ensemble de données.

Il existe quatre manières courantes de créer une matrice de corrélation dans R :

Méthode 1 : la fonction cor (pour obtenir une matrice simple de coefficients de corrélation)

cor(df)

Méthode 2 : la fonction rcorr (pour obtenir les valeurs p des coefficients de corrélation)

library(Hmisc)

rcorr(as.matrix(df))

Méthode 3 : la fonction corrplot (pour visualiser la matrice de corrélation)

library(corrplot)

corrplot(cor(df))

Méthode 4 : la fonction ggcorrplot (pour visualiser la matrice de corrélation)

library(ggcorrplot)

ggcorrplot(cor(df))

Les exemples suivants montrent comment utiliser chaque méthode avec le bloc de données suivant dans R :

#create data frame
df <- data.frame(assists=c(4, 5, 5, 6, 7, 8, 8, 10),
                 rebounds=c(12, 14, 13, 7, 8, 8, 9, 13),
                 points=c(22, 24, 26, 26, 29, 32, 20, 14))

#view data frame
df

  assists rebounds points
1       4       12     22
2       5       14     24
3       5       13     26
4       6        7     26
5       7        8     29
6       8        8     32
7       8        9     20
8      10       13     14

Exemple 1 : La fonction cor

Nous pouvons utiliser la fonction cor() de la base R pour créer une matrice de corrélation qui montre les coefficients de corrélation entre chaque variable de notre bloc de données :

#create correlation matrix
cor(df)

            assists   rebounds     points
assists   1.0000000 -0.2448608 -0.3295730
rebounds -0.2448608  1.0000000 -0.5220917
points   -0.3295730 -0.5220917  1.0000000

Les coefficients de corrélation le long de la diagonale du tableau sont tous égaux à 1 car chaque variable est parfaitement corrélée avec elle-même.

Tous les autres coefficients de corrélation indiquent la corrélation entre différentes combinaisons de variables par paires. Par exemple:

• Le coefficient de corrélation entre passes décisives et rebonds est de -0,245 .
• Le coefficient de corrélation entre les passes décisives et les points est de -0,330 .
• Le coefficient de corrélation entre rebonds et points est de -0,522 .

Exemple 2 : la fonction rcorr

Nous pouvons utiliser la fonction rcorr() du package Hmisc dans R pour créer une matrice de corrélation qui montre les coefficients de corrélation entre chaque variable de notre bloc de données :

library(Hmisc)

#create matrix of correlation coefficients and p-values
rcorr(as.matrix(df))

         assists rebounds points
assists     1.00    -0.24  -0.33
rebounds   -0.24     1.00  -0.52
points     -0.33    -0.52   1.00

n= 8 

P
         assists rebounds points
assists          0.5589   0.4253
rebounds 0.5589           0.1844
points   0.4253  0.1844 

La première matrice montre les coefficients de corrélation entre les variables et la deuxième matrice montre les valeurs p correspondantes.

Par exemple, le coefficient de corrélation entre les passes décisives et les rebonds est de -0,24 et la valeur p de ce coefficient de corrélation est de 0,5589 .

Cela nous indique que la corrélation entre les deux variables est négative mais ce n’est pas une corrélation statistiquement significative puisque la valeur p n’est pas inférieure à 0,05.

Exemple 3 : La fonction corrplot

Nous pouvons utiliser la fonction corrplot() du package corrplot dans R pour visualiser la matrice de corrélation :

library(corrplot)

#visualize correlation matrix
corrplot(cor(df))

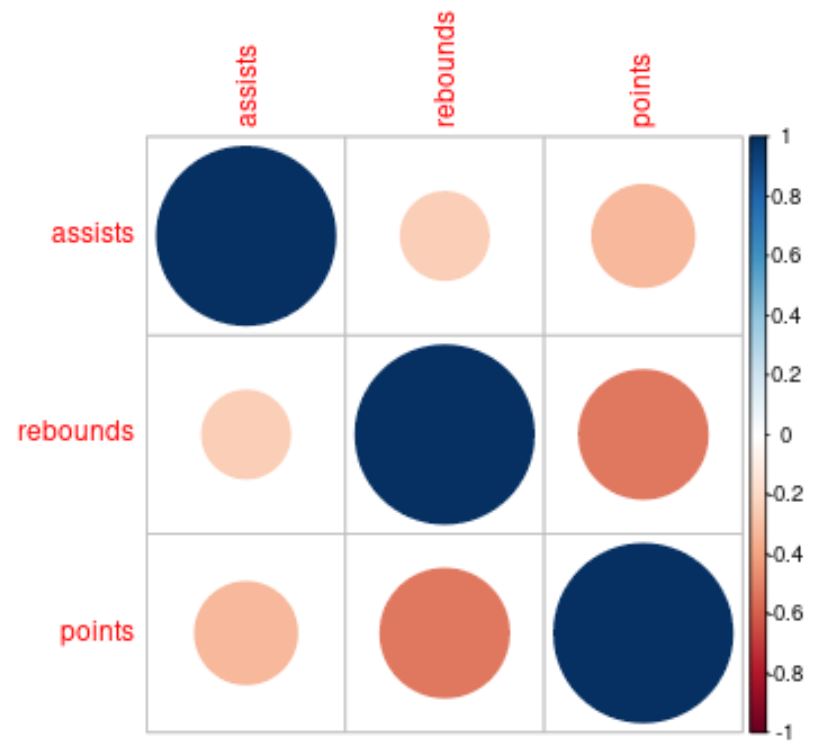
La couleur et la taille des cercles dans la matrice de corrélation nous aident à visualiser les corrélations entre chaque variable.

Par exemple, le cercle où se croisent les variables de passes décisives et de rebonds est petit et rouge clair, ce qui nous indique que la corrélation est faible et négative.

Exemple 4 : La fonction corrplot

Nous pouvons utiliser la fonction ggcorrplot() du package ggcorrplot dans R pour visualiser la matrice de corrélation :

library(ggcorrplot)

#visualize correlation matrix
ggcorrplot(cor(df))

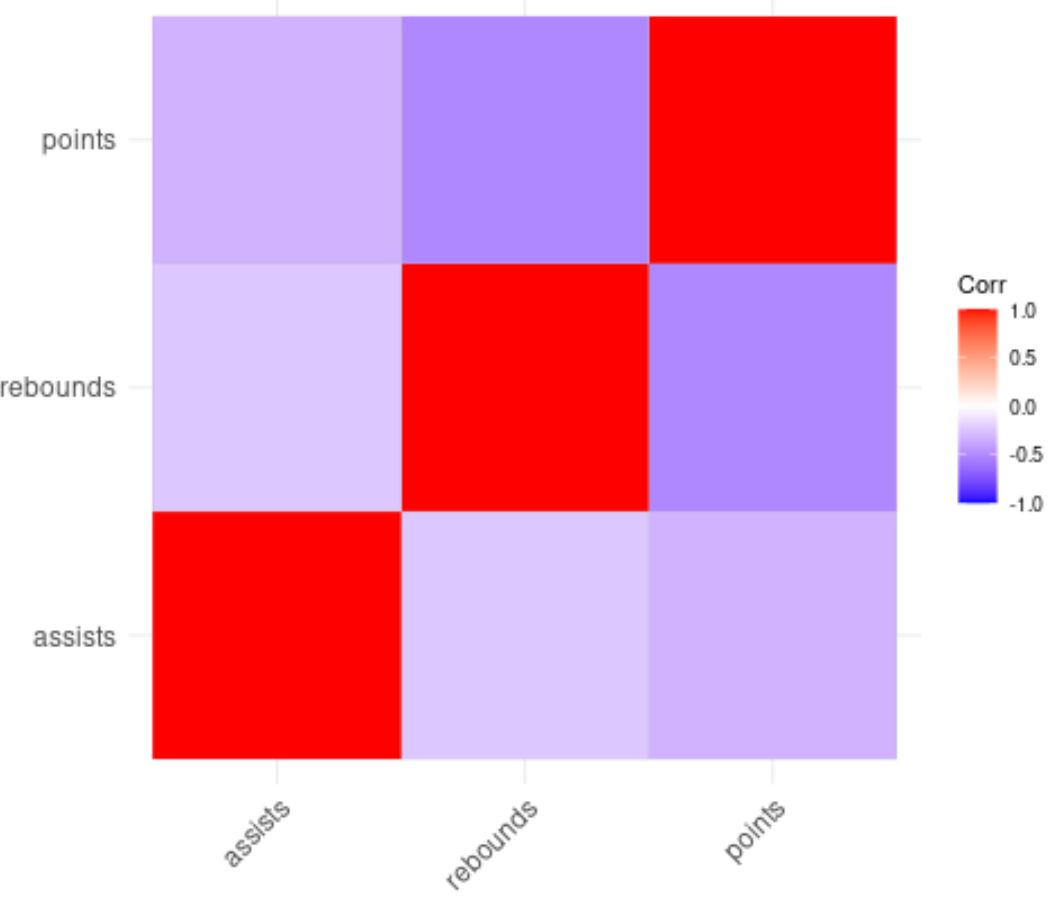
La couleur des carrés de la matrice de corrélation nous aide à visualiser les corrélations entre chaque variable.

Ressources additionnelles

Les didacticiels suivants expliquent comment effectuer d’autres tâches courantes dans R :

Comment calculer la corrélation de rang de Spearman dans R
Comment calculer la corrélation partielle dans R
Comment calculer la corrélation glissante dans R