Comment créer et interpréter une matrice de corrélation dans Excel

Une façon de quantifier la relation entre deux variables consiste à utiliser le coefficient de corrélation de Pearson , qui est une mesure de l’association linéaire entre deux variables .

Il a une valeur comprise entre -1 et 1 où :

• -1 indique une corrélation linéaire parfaitement négative entre deux variables
• 0 indique aucune corrélation linéaire entre deux variables
• 1 indique une corrélation linéaire parfaitement positive entre deux variables

Plus le coefficient de corrélation s’éloigne de zéro, plus la relation entre les deux variables est forte.

Mais dans certains cas, nous souhaitons comprendre la corrélation entre plusieurs paires de variables.

Dans ces cas, nous pouvons créer une matrice de corrélation , qui est un tableau carré qui montre les coefficients de corrélation entre plusieurs combinaisons de variables par paires.

Ce tutoriel explique comment créer et interpréter une matrice de corrélation dans Excel.

Comment créer une matrice de corrélation dans Excel

Supposons que nous ayons l’ensemble de données suivant qui montre le nombre moyen de points, de rebonds et de passes décisives pour 10 joueurs de basket-ball :

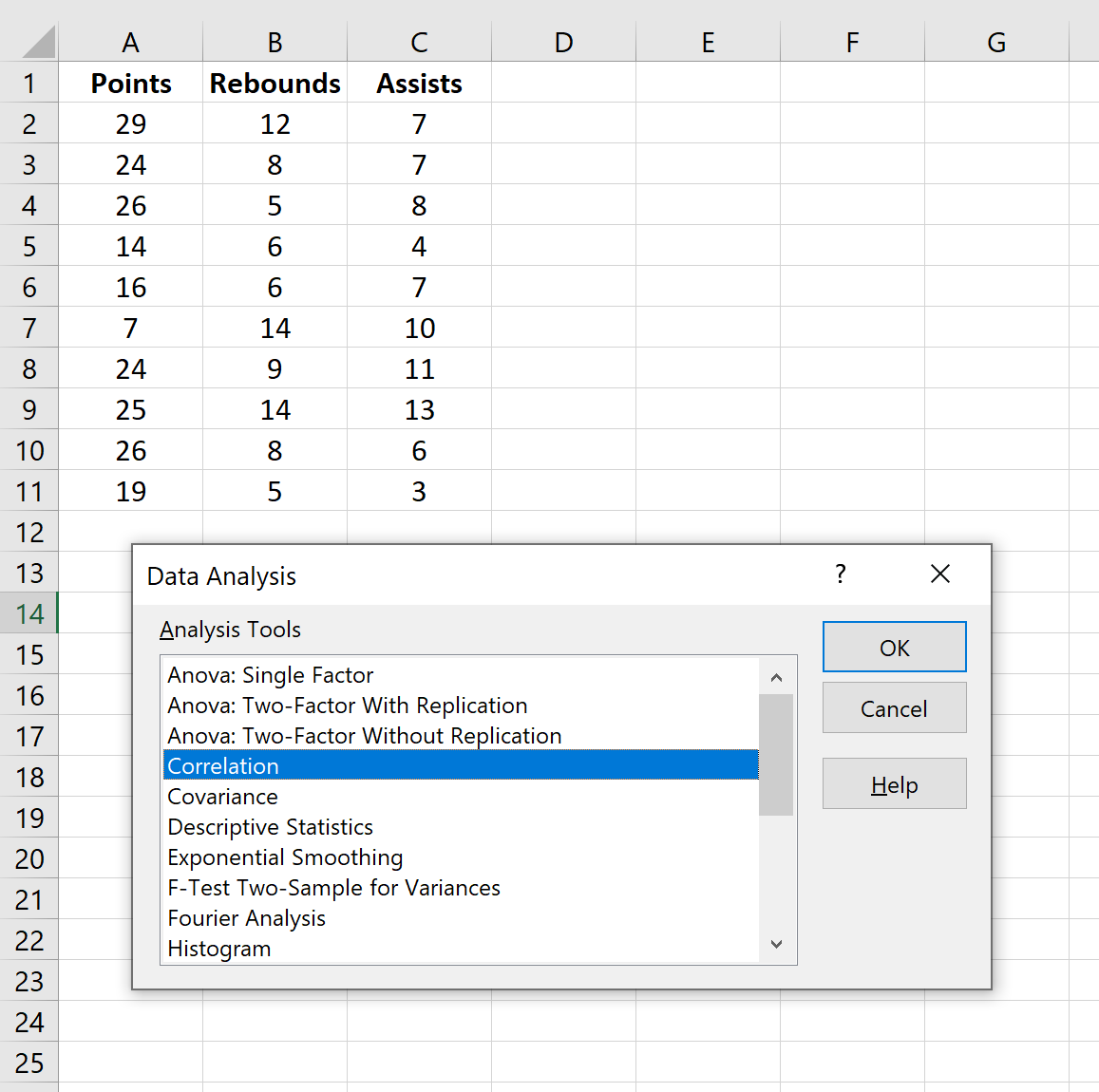
Pour créer une matrice de corrélation pour cet ensemble de données, accédez à l’onglet Données dans le ruban supérieur d’Excel et cliquez sur Analyse des données .

Si vous ne voyez pas cette option, vous devez d’abord charger le Data Analysis Toolpak gratuit dans Excel .

Dans la nouvelle fenêtre qui apparaît, sélectionnez Corrélation et cliquez sur OK .

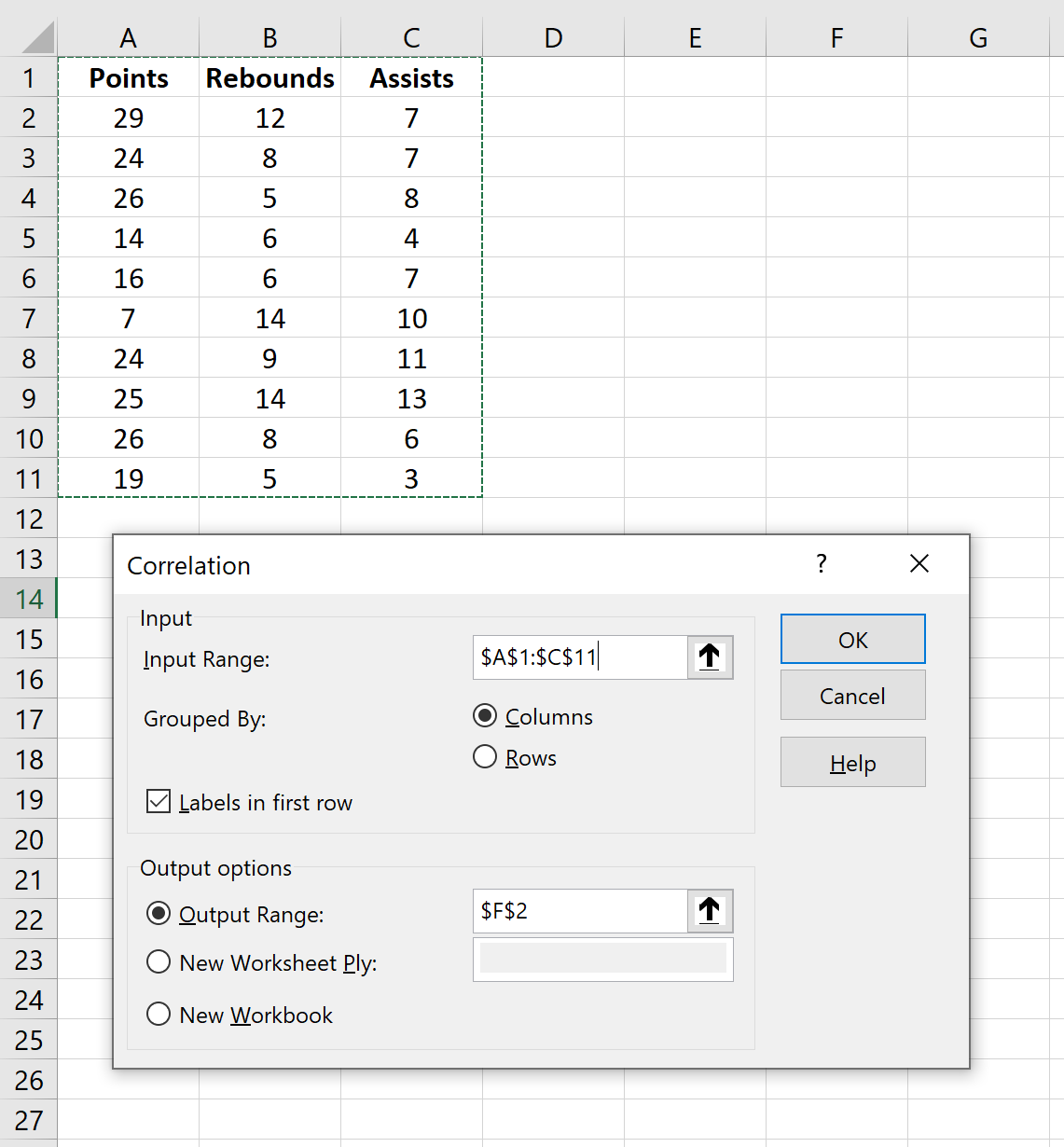
Pour Plage d’entrée , sélectionnez les cellules où se trouvent les données (y compris la première ligne avec les étiquettes). Cochez la case à côté de Étiquettes dans la première ligne . Pour Plage de sortie , sélectionnez une cellule dans laquelle vous souhaitez que la matrice de corrélation apparaisse. Cliquez ensuite sur OK .

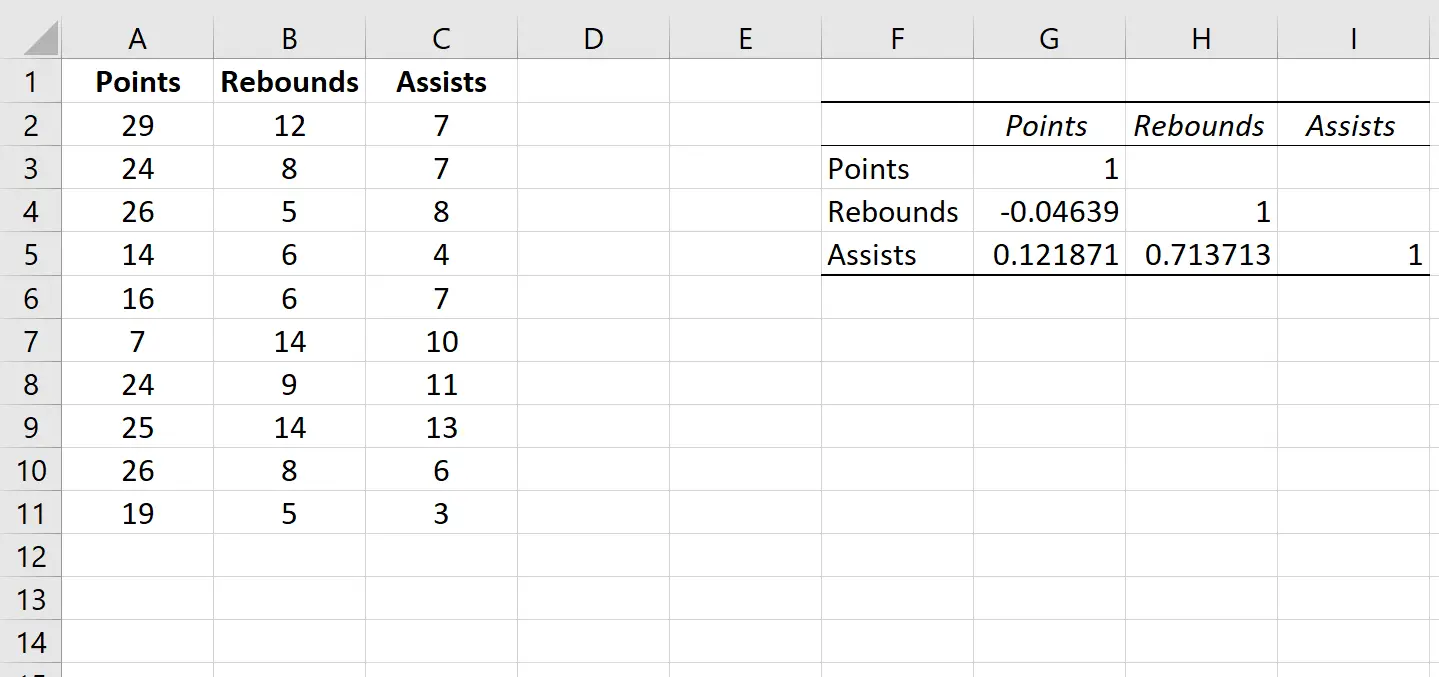
Cela produira automatiquement la matrice de corrélation suivante :

Comment interpréter une matrice de corrélation dans Excel

Les valeurs dans les cellules individuelles de la matrice de corrélation nous indiquent le coefficient de corrélation de Pearson entre chaque combinaison de variables par paire. Par exemple:

Corrélation entre points et rebonds : -0,04639. Les points et les rebonds sont légèrement corrélés négativement, mais cette valeur est si proche de zéro qu’il n’existe pas de preuves solides d’une association significative entre ces deux variables.

Corrélation entre points et passes décisives : 0,121871. Les points et les passes décisives sont légèrement corrélés positivement, mais cette valeur est également assez proche de zéro, il n’existe donc pas de preuves solides d’une association significative entre ces deux variables.

Corrélation entre rebonds et passes décisives : 0,713713. Les rebonds et les passes décisives sont fortement corrélés positivement. Autrement dit, les joueurs qui ont plus de rebonds ont également tendance à avoir plus de passes décisives.

Notez que les valeurs diagonales de la matrice de corrélation sont toutes égales à 1 car la corrélation entre une variable et elle-même est toujours 1. En pratique, ce nombre n’est pas utile à interpréter.

Bonus : Visualiser les coefficients de corrélation

Un moyen simple de visualiser la valeur des coefficients de corrélation dans le tableau consiste à appliquer un formatage conditionnel au tableau.

Dans le ruban supérieur d’Excel, accédez à l’onglet Accueil , puis au groupe Styles .

Cliquez sur Graphique de mise en forme conditionnelle , puis sur Échelles de couleurs , puis sur Échelle de couleurs vert-jaune-rouge .

Cela applique automatiquement l’échelle de couleurs suivante à la matrice de corrélation :

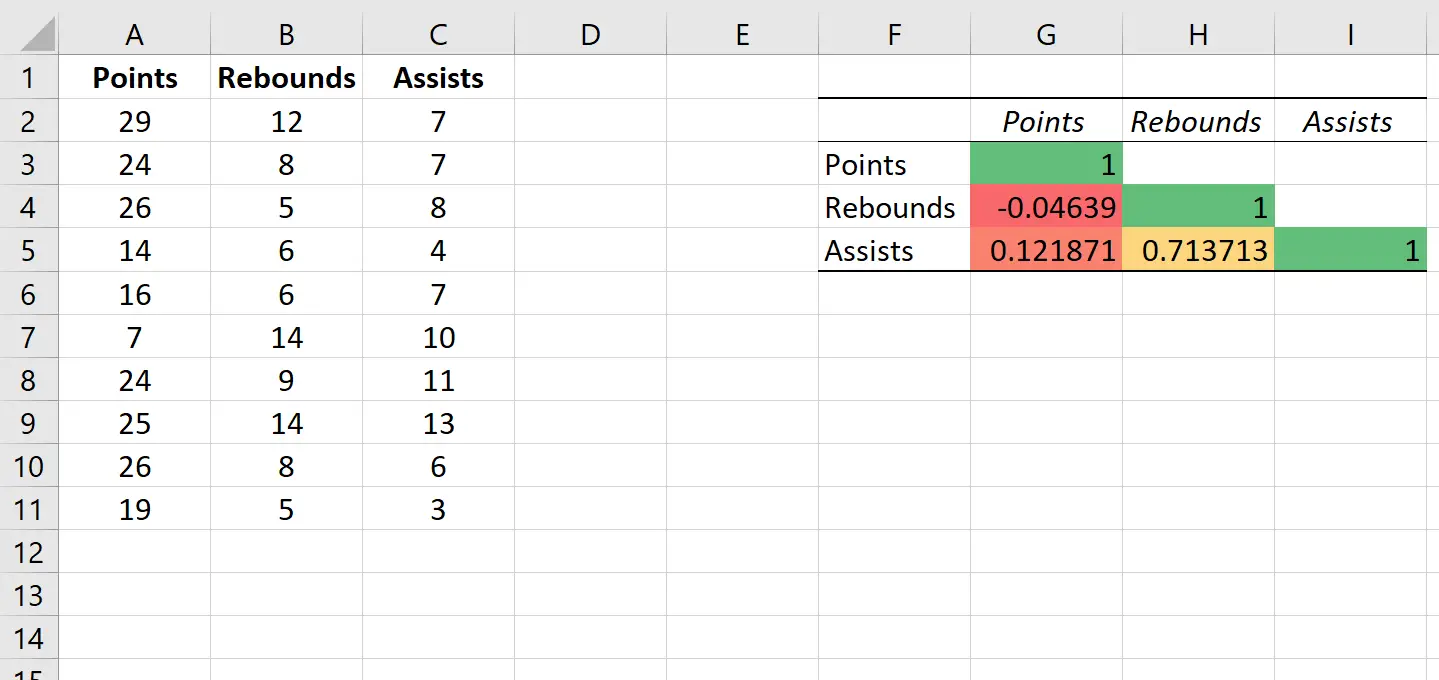
Cela nous aide à visualiser facilement la force des corrélations entre les variables.

C’est une astuce particulièrement utile si nous travaillons avec une matrice de corrélation comportant de nombreuses variables, car elle nous aide à identifier rapidement les variables qui ont les corrélations les plus fortes.

Connexes : Qu’est-ce qui est considéré comme une corrélation « forte » ?

Ressources additionnelles

Les didacticiels suivants expliquent comment effectuer d’autres tâches courantes dans R :

Comment créer une matrice de nuages de points dans Excel
Comment effectuer un test de corrélation dans Excel