Comment créer une matrice de corrélation en Python

Une façon de quantifier la relation entre deux variables consiste à utiliser le coefficient de corrélation de Pearson , qui est une mesure de l’association linéaire entre deux variables .

Il prend une valeur comprise entre -1 et 1 où :

• -1 indique une corrélation linéaire parfaitement négative.
• 0 indique aucune corrélation linéaire.
• 1 indique une corrélation linéaire parfaitement positive.

Plus le coefficient de corrélation s’éloigne de zéro, plus la relation entre les deux variables est forte.

Mais dans certains cas, nous souhaitons comprendre la corrélation entre plusieurs paires de variables. Dans ces cas, nous pouvons créer une matrice de corrélation , qui est un tableau carré qui montre les coefficients de corrélation entre plusieurs combinaisons de variables par paires.

Ce tutoriel explique comment créer et interpréter une matrice de corrélation en Python.

Comment créer une matrice de corrélation en Python

Utilisez les étapes suivantes pour créer une matrice de corrélation en Python.

Étape 1 : Créez l’ensemble de données.

import pandas as pd

data = {'assists': [4, 5, 5, 6, 7, 8, 8, 10],
        'rebounds': [12, 14, 13, 7, 8, 8, 9, 13],
        'points': [22, 24, 26, 26, 29, 32, 20, 14]
        }

df = pd.DataFrame(data, columns=['assists','rebounds','points'])
df

   assist  rebounds  points
0	4	12	22
1	5	14	24
2	5	13	26
3	6	7	26
4	7	8	29
5	8	8	32
6	8	9	20
7	10	13	14

Étape 2 : Créez la matrice de corrélation.

#create correlation matrix
df.corr()

                assists   rebounds     points
assists        1.000000  -0.244861  -0.329573
rebounds      -0.244861   1.000000  -0.522092
points        -0.329573  -0.522092   1.000000

#create same correlation matrix with coefficients rounded to 3 decimals 
df.corr().round(3)
	       assists	rebounds  points
assists	         1.000	  -0.245  -0.330
rebounds	-0.245	   1.000  -0.522
points	        -0.330	  -0.522   1.000

Étape 3 : Interpréter la matrice de corrélation.

Les coefficients de corrélation le long de la diagonale du tableau sont tous égaux à 1 car chaque variable est parfaitement corrélée avec elle-même.

Tous les autres coefficients de corrélation indiquent la corrélation entre différentes combinaisons de variables par paires. Par exemple:

• Le coefficient de corrélation entre passes décisives et rebonds est de -0,245 .
• Le coefficient de corrélation entre les passes décisives et les points est de -0,330 .
• Le coefficient de corrélation entre rebonds et points est de -0,522 .

Étape 4 : Visualisez la matrice de corrélation (facultatif).

Vous pouvez visualiser la matrice de corrélation en utilisant les options de style disponibles dans pandas :

corr = df.corr()
corr.style.background_gradient(cmap='coolwarm')

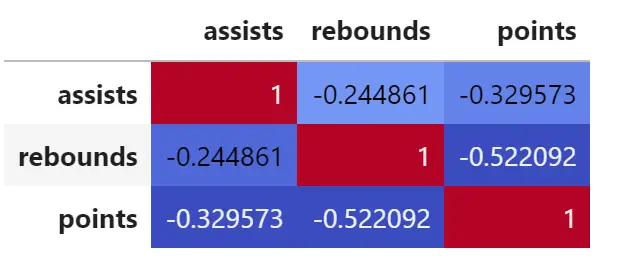
Vous pouvez également modifier l’argument de cmap pour produire une matrice de corrélation avec différentes couleurs.

corr = df.corr()
corr.style.background_gradient(cmap='RdYlGn')

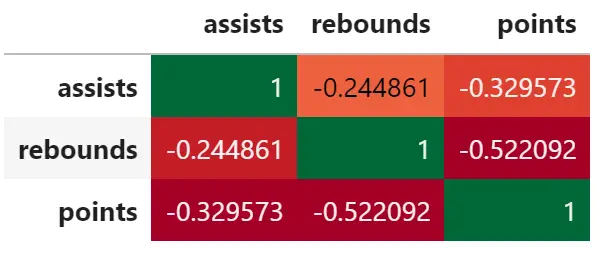
corr = df.corr()
corr.style.background_gradient(cmap='bwr')

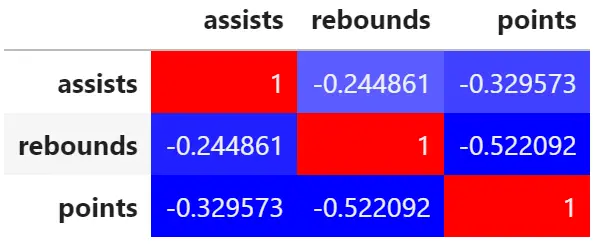
corr = df.corr()
corr.style.background_gradient(cmap='PuOr')

Remarque : Pour une liste complète des arguments cmap , reportez-vous à la documentation matplotlib .