Comment créer une matrice de covariance dans SPSS

La covariance est une mesure de la façon dont les changements dans une variable sont associés aux changements dans une deuxième variable. Plus précisément, il s’agit d’une mesure du degré auquel deux variables sont linéairement associées.

La formule pour calculer la covariance entre deux variables, X et Y est :

COV( X , Y ) = Σ(x- x )(y- y ) / n

Une matrice de covariance est une matrice carrée qui montre la covariance entre différentes variables d’un ensemble de données.

Ce didacticiel explique comment créer une matrice de covariance pour un ensemble de données donné dans SPSS.

Exemple : Matrice de covariance dans SPSS

Supposons que nous disposions de l’ensemble de données suivant qui montre les résultats aux tests de 10 élèves différents dans trois matières : mathématiques, sciences et histoire :

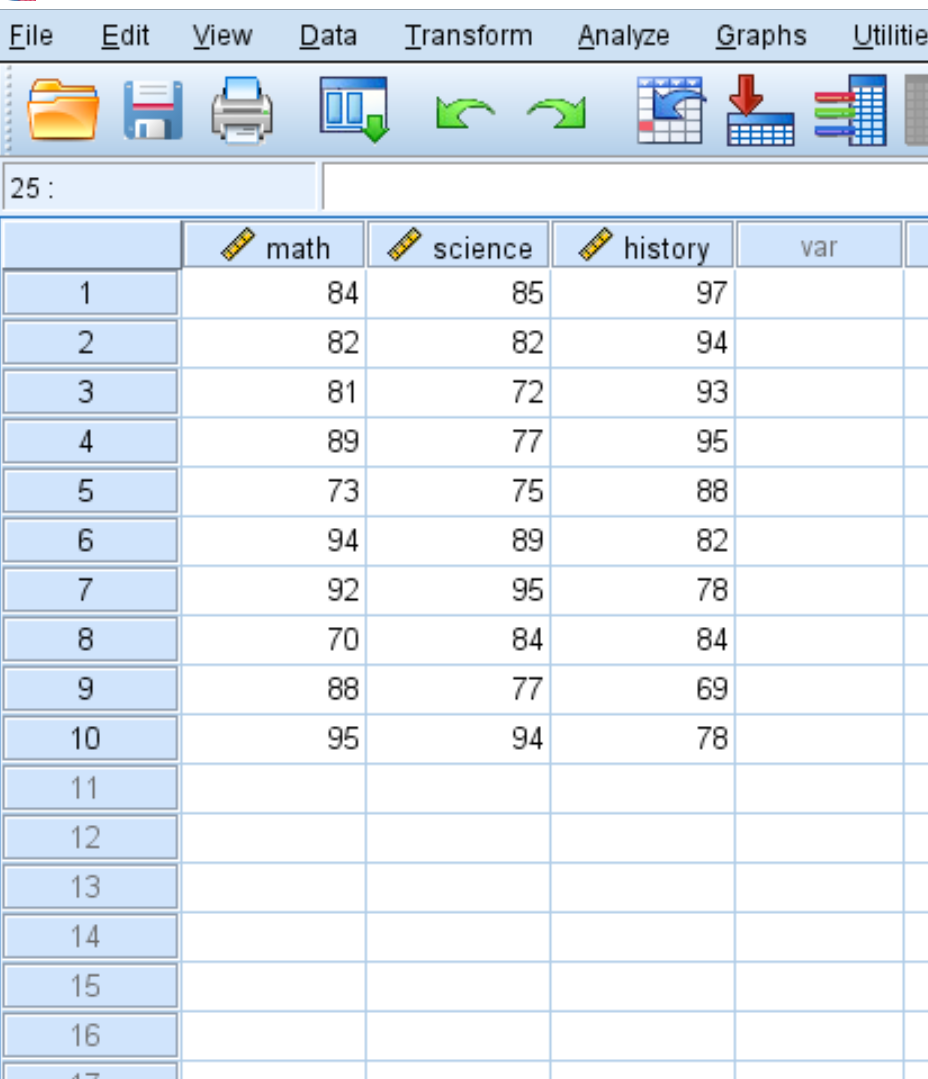
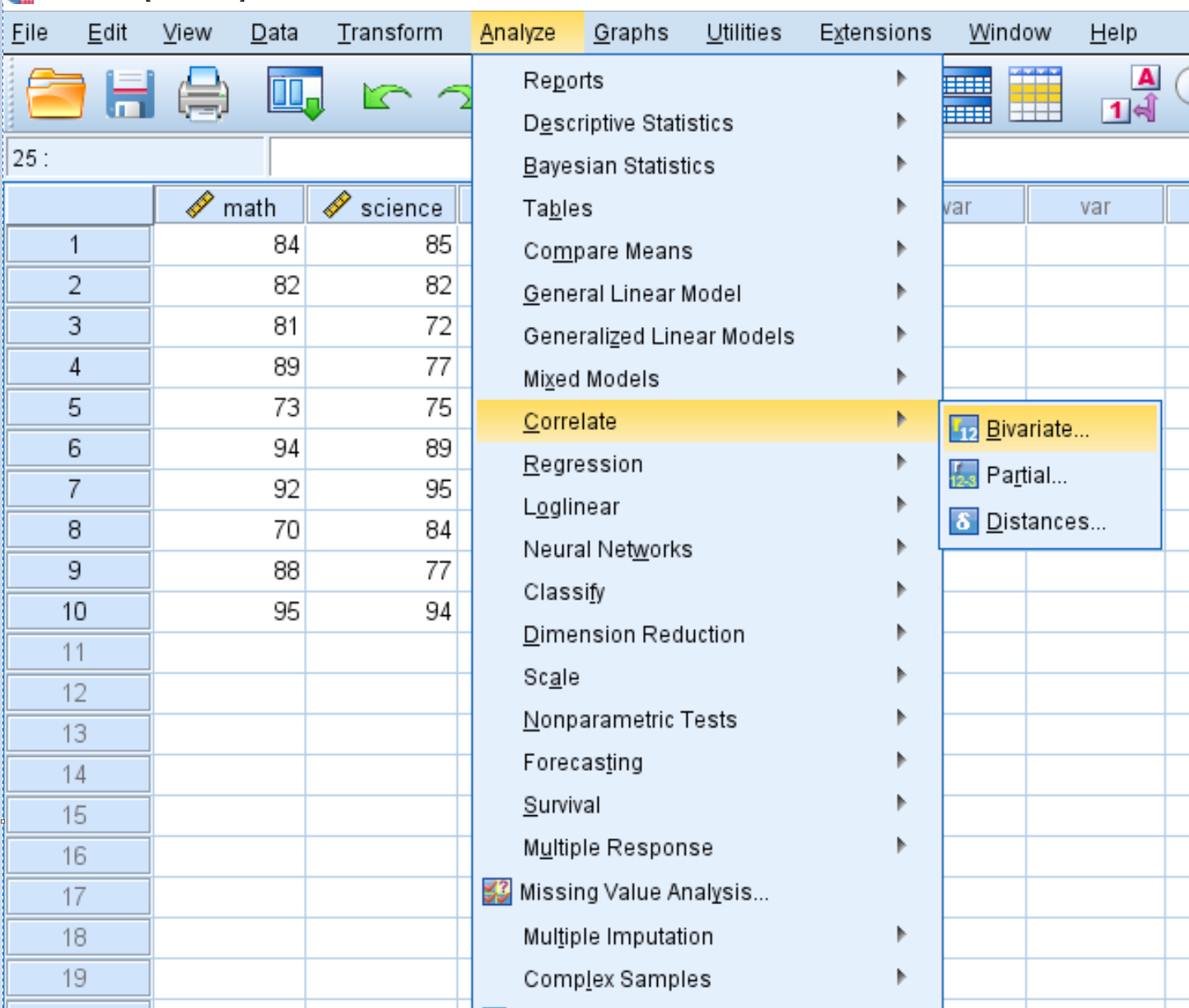
Pour créer une matrice de covariance pour cet ensemble de données, cliquez sur l’onglet Analyser , puis Corréler , puis Bivarier :

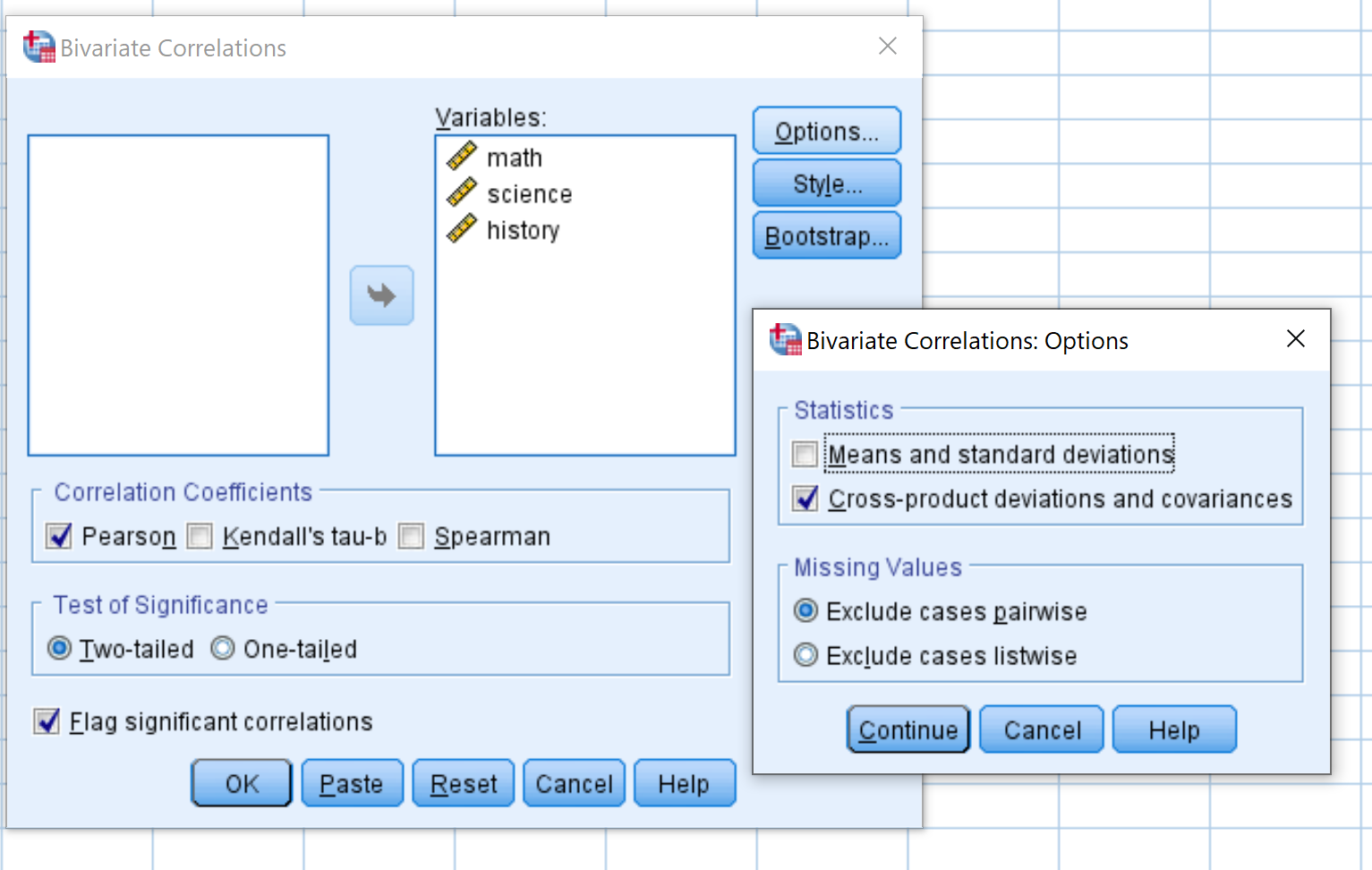
Dans la nouvelle fenêtre qui apparaît, faites glisser chacune des trois variables dans la case intitulée Variables :

Ensuite, cliquez sur Options . Cochez la case à côté de Écarts et covariances entre produits . Cliquez ensuite sur Continuer .

Cliquez ensuite sur OK . Le résultat apparaîtra dans une nouvelle fenêtre :

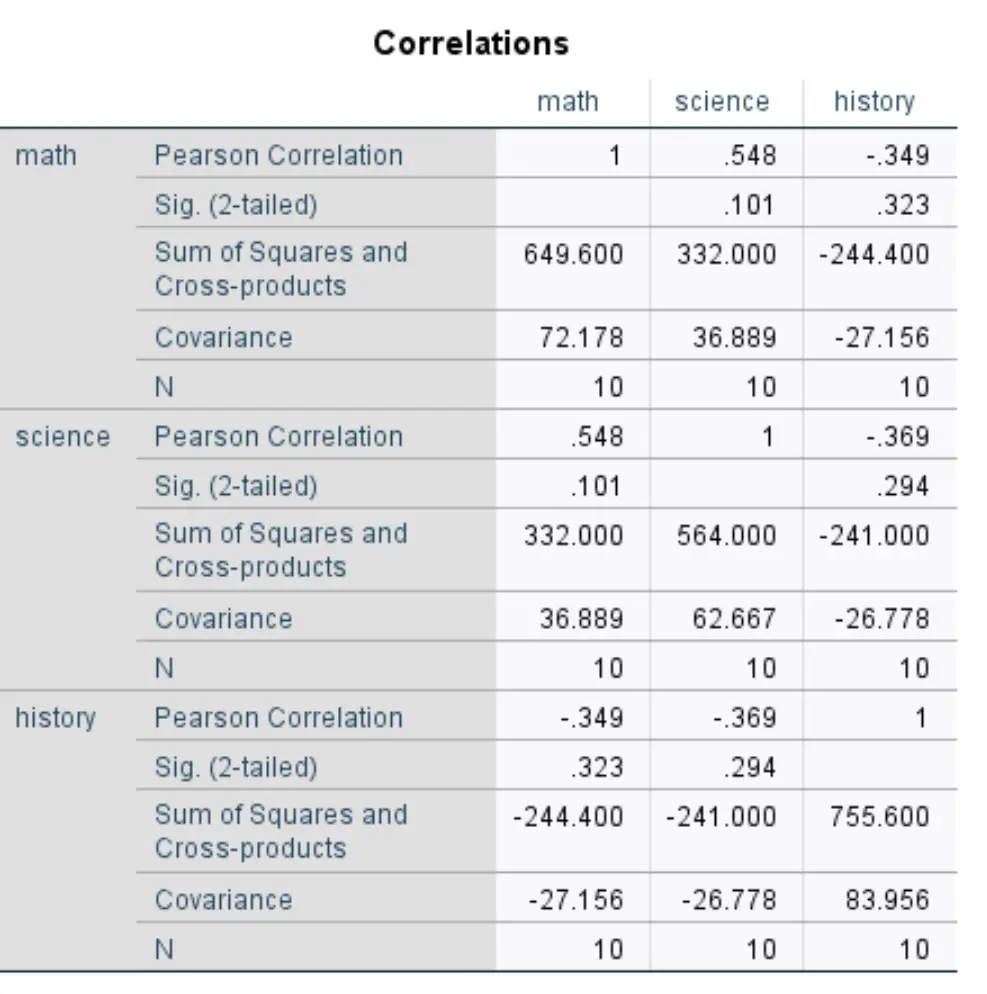
Pour obtenir la covariance pour chaque combinaison par paire de variables, vous devez diviser la somme des carrés et des produits vectoriels par N .

Par exemple, la covariance entre les mathématiques et les sciences peut être calculée comme suit :

COV(mathématiques, sciences) = 332 000 / 10 = 33,2 .

De même, la covariance entre les mathématiques et l’histoire peut être calculée comme suit :

COV(mathématiques, histoire) = -244,400 / 10 = -24,44 .

Vous pouvez également obtenir la variance pour chaque variable en divisant la somme des carrés et des produits vectoriels par N .

Par exemple, la variance en mathématiques peut être calculée comme suit :

VAR(mathématiques) = 649,600 / 10 = 64,96 .

Vous pouvez obtenir la matrice de covariance complète pour cet ensemble de données en effectuant des calculs similaires :

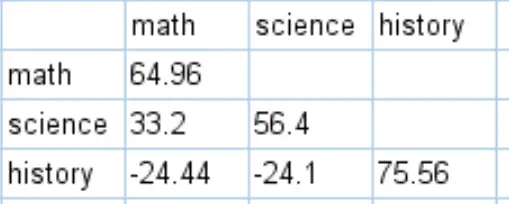
Comment interpréter une matrice de covariance

Les valeurs le long des diagonales de la matrice de covariance sont simplement les variances de chaque sujet. Par exemple:

• La variance des résultats en mathématiques est de 64,96 .
• La variance des scores en sciences est de 56,4 .
• La variance des scores historiques est de 75,56 .

Les autres valeurs de la matrice représentent les covariances entre les différents sujets. Par exemple:

• La covariance entre les scores en mathématiques et en sciences est de 33,2 .
• La covariance entre les scores en mathématiques et en histoire est de -24,44 .
• La covariance entre les scores en sciences et en histoire est de -24,1 .

Un nombre positif pour la covariance indique que deux variables ont tendance à augmenter ou diminuer en tandem. Par exemple, les mathématiques et les sciences ont une covariance positive (33,2), ce qui indique que les élèves qui obtiennent des résultats élevés en mathématiques ont également tendance à obtenir des résultats élevés en sciences. De même, les élèves qui obtiennent de faibles résultats en mathématiques ont également tendance à obtenir de faibles résultats en sciences.

Un nombre négatif pour la covariance indique que lorsqu’une variable augmente, une deuxième variable a tendance à diminuer. Par exemple, les sciences et l’histoire ont une covariance négative (-24,1), ce qui indique que les élèves qui obtiennent des résultats élevés en sciences ont tendance à avoir des résultats faibles en histoire. De même, les élèves qui obtiennent de faibles résultats en sciences ont tendance à obtenir des résultats élevés en histoire.

Ressources additionnelles

Comment créer une matrice de corrélation dans SPSS
Comment calculer la corrélation partielle dans SPSS