Comment trouver la médiane des données groupées : avec des exemples

Nous souhaitons souvent calculer la médiane des données regroupées d’une manière ou d’une autre.

Rappelons que la médiane représente la valeur qui se situe directement au milieu d’un ensemble de données, lorsque toutes les valeurs sont classées de la plus petite à la plus grande.

Par exemple, supposons que nous disposions des données groupées suivantes :

Bien qu’il ne soit pas possible de calculer la médiane exacte puisque nous ne connaissons pas les valeurs des données brutes , il est possible d’estimer la médiane à l’aide de la formule suivante :

Médiane des données groupées = L + W[(N/2 – C) / F]

où:

• L : Limite inférieure de la classe médiane
• W : Largeur de la classe médiane
• N : Fréquence totale
• C : Fréquence cumulée jusqu’à la classe médiane
• F : Fréquence de classe médiane

Remarque : La classe médiane est la classe qui contient la valeur située à N/2. Dans l’exemple ci-dessus, il y a N = 23 valeurs totales. Ainsi, la valeur médiane est celle en position 23/2 = 11,5, qui se situerait dans la classe 21-30.

Les exemples suivants montrent comment calculer la médiane des données groupées dans différents scénarios.

Exemple 1 : calculer la médiane des données groupées

Supposons que nous ayons la distribution de fréquence suivante qui montre l’examen noté par 40 étudiants dans une certaine classe :

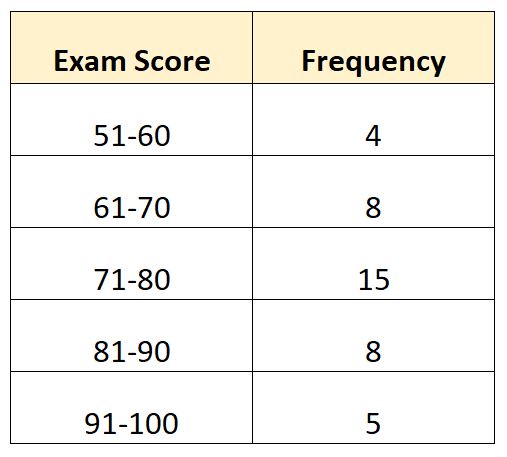
Dans cet exemple, il y a N = 40 valeurs totales. Ainsi, la valeur médiane se situe dans la classe où se situe 40/2 = 20. La 20e plus grande valeur se situerait dans la classe 71-80 .

Sachant cela, nous pouvons calculer les valeurs suivantes :

• L : Limite inférieure de classe médiane : 71
• W : Largeur de classe médiane : 9
• N : Fréquence totale : 40
• C : Fréquence cumulée jusqu’à la classe médiane : 12
• F : Fréquence de classe médiane : 15

Nous pouvons intégrer ces valeurs dans la formule pour calculer la médiane de la distribution :

• Médiane = L + W[(N/2 – C) / F]
• Médiane = 71 + 9[(40/2 – 12) / 15]
• Médiane = 75,8

Nous estimons que la note médiane à l’examen est de 75,8 .

Exemple 2 : calculer la médiane des données groupées

Supposons que nous ayons la distribution de fréquence suivante qui montre le nombre de points marqués par match par 60 joueurs de basket-ball :

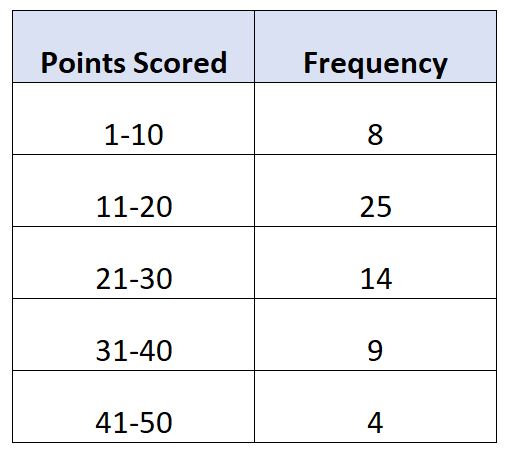
Dans cet exemple, il y a N = 60 valeurs totales. Ainsi, la valeur médiane se situe dans la classe où se situe 60/2 = 30. La 30ème plus grande valeur se situerait dans la classe 11-20 .

Sachant cela, nous pouvons calculer les valeurs suivantes :

• L : Limite inférieure de classe médiane : 11
• W : Largeur de classe médiane : 9
• N : Fréquence totale : 60
• C : Fréquence cumulée jusqu’à la classe médiane : 8
• F : Fréquence de classe médiane : 25

Nous pouvons intégrer ces valeurs dans la formule pour calculer la médiane de la distribution :

• Médiane = L + W[(N/2 – C) / F]
• Médiane = 11 + 9[(60/2 – 8) / 25]
• Médiane = 18,92

Nous estimons que la note médiane à l’examen est de 18,92 .

Ressources additionnelles

Les didacticiels suivants expliquent comment effectuer d’autres opérations courantes avec des données groupées :

Comment trouver la moyenne et l’écart type des données groupées
Comment trouver le mode des données groupées
Comment calculer le classement centile pour les données groupées