Les trois hypothèses de l’ANOVA à mesures répétées

Une ANOVA à mesures répétées est utilisée pour déterminer s’il existe ou non une différence statistiquement significative entre les moyennes de trois groupes ou plus dans lesquels les mêmes sujets apparaissent dans chaque groupe.

Cependant, avant d’effectuer une ANOVA à mesures répétées, nous devons nous assurer que les hypothèses suivantes sont remplies :

1. Indépendance : Chacune des observations doit être indépendante.

2. Normalité : La distribution de la variable de réponse est normalement distribuée.

3. Sphéricité : Les variances des différences entre toutes les combinaisons de groupes apparentés doivent être égales.

Si une ou plusieurs de ces hypothèses ne sont pas respectées, les résultats de l’ANOVA à mesures répétées peuvent ne pas être fiables.

Dans cet article, nous fournissons une explication pour chaque hypothèse, comment déterminer si l’hypothèse est satisfaite et que faire si elle n’est pas respectée.

Hypothèse 1 : Indépendance

Une ANOVA à mesures répétées suppose que chaque observation de votre ensemble de données est indépendante de toutes les autres observations.

Comment déterminer si cette hypothèse est remplie

Le moyen le plus simple de vérifier cette hypothèse est de vérifier que chaque individu de l’ensemble de données a été échantillonné au hasard dans la population en utilisant une méthode d’échantillonnage aléatoire .

Si une méthode d’échantillonnage aléatoire a été utilisée, on peut supposer que chaque observation est indépendante.

Que faire si cette hypothèse n’est pas respectée

Si cette hypothèse n’est pas respectée, il s’agit alors d’un problème grave car les valeurs de chaque individu peuvent être liées les unes aux autres d’une manière ou d’une autre.

Souvent, le seul remède dans ce scénario consiste à recruter des individus pour une nouvelle étude en utilisant une méthode d’échantillonnage aléatoire.

Hypothèse 2 : normalité

Une ANOVA à mesures répétées suppose que la distribution de la variable de réponse est normalement distribuée .

Comment déterminer si cette hypothèse est remplie

Il existe deux manières de vérifier si cette hypothèse est vérifiée :

1. Créez un histogramme ou un tracé QQ

Vous pouvez vérifier visuellement si la distribution de la variable de réponse est à peu près normalement distribuée en créant un histogramme ou un tracé QQ.

Si vous créez un histogramme , vérifiez simplement que la distribution de la variable de réponse suit approximativement une forme de « cloche ». Si tel est le cas, vous pouvez souvent supposer que l’hypothèse de normalité est remplie :

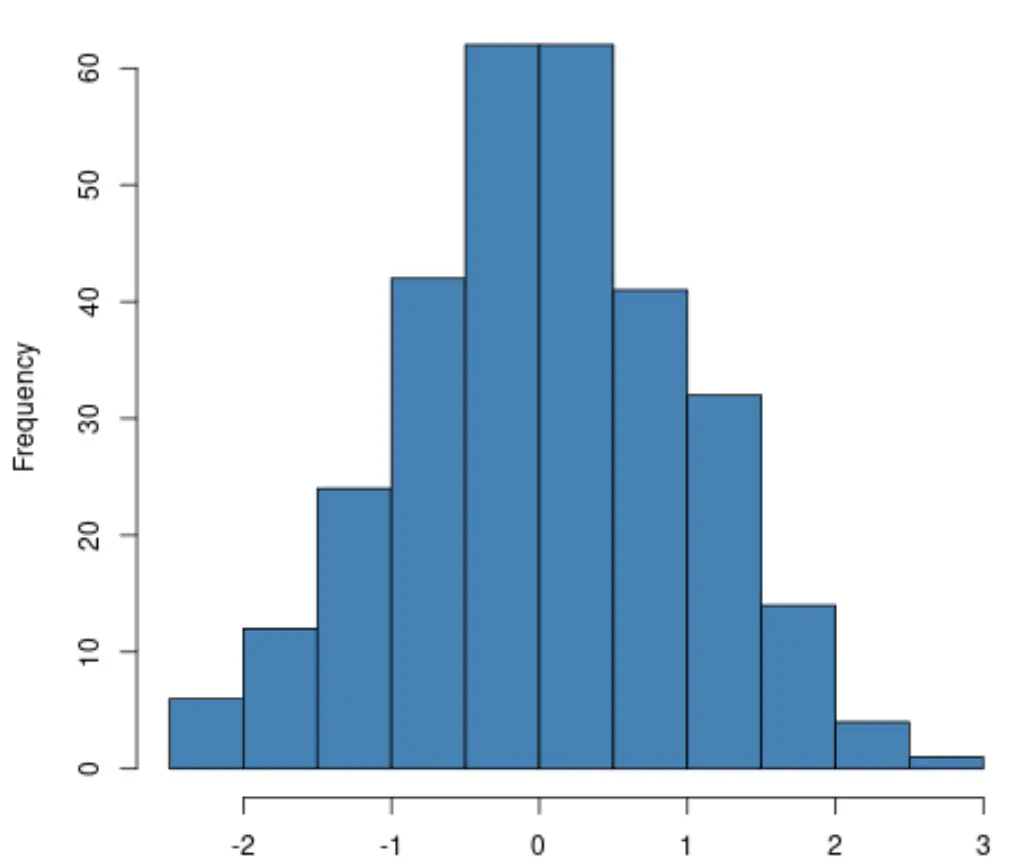
Si vous créez un tracé QQ , vérifiez si les points de données se situent le long d’une ligne diagonale droite. Si tel est le cas, vous pouvez généralement supposer que l’hypothèse de normalité est remplie :

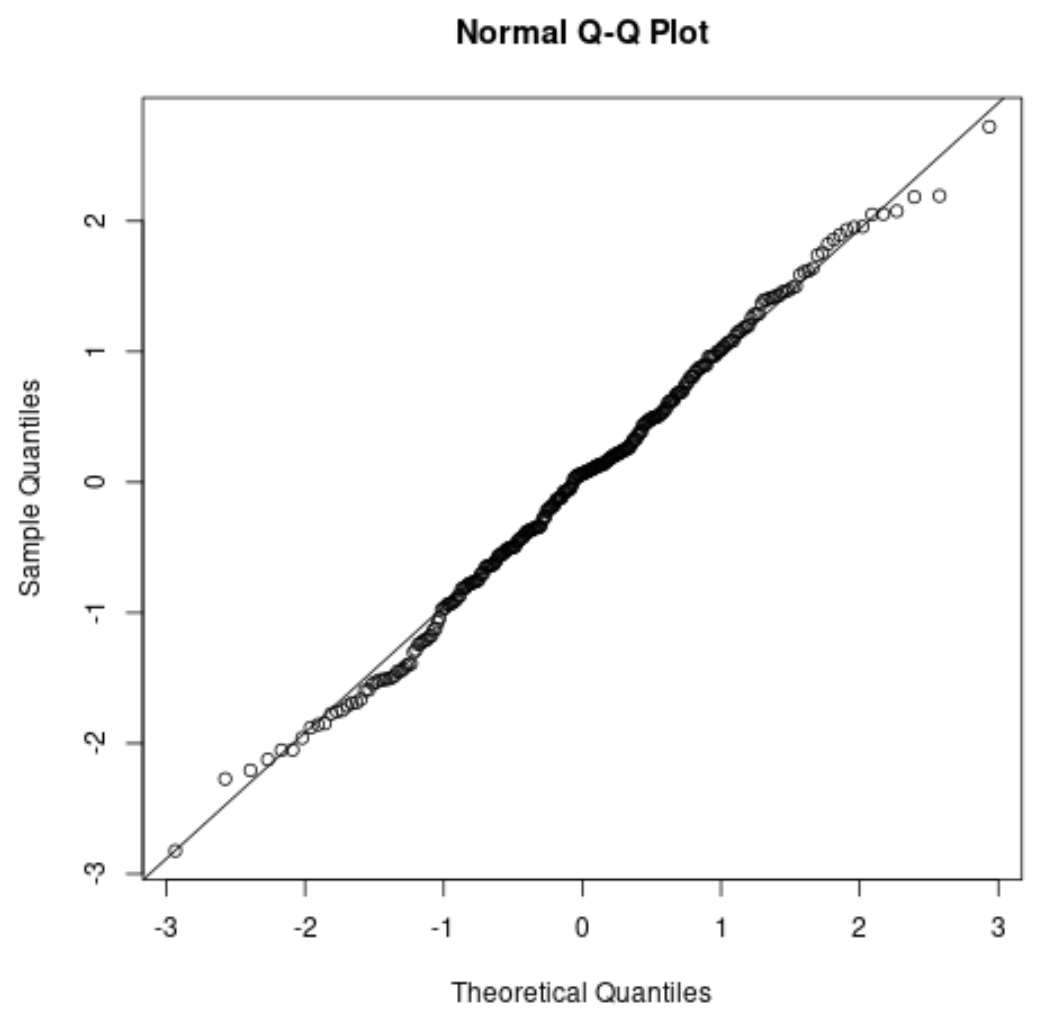
Connexe : Comment utiliser les tracés QQ pour vérifier la normalité

2. Effectuer un test statistique formel

Vous pouvez également effectuer un test Shapiro-Wilk pour vérifier la normalité. Si la valeur p du test est inférieure à 0,05, cela suggère que les données ne sont pas distribuées normalement.

Cependant, sachez que lorsque vous travaillez avec des échantillons extrêmement grands, les tests statistiques comme le test de Shapiro-Wilk vous indiqueront presque toujours que vos données ne sont pas normales.

Pour cette raison, il est souvent préférable d’inspecter visuellement vos données à l’aide de graphiques tels que des histogrammes et des tracés QQ. En regardant simplement les graphiques, vous pouvez avoir une assez bonne idée de si les données sont normalement distribuées ou non.

Que faire si cette hypothèse n’est pas respectée

En général, une ANOVA à mesures répétées est considérée comme assez robuste contre les violations de l’hypothèse de normalité tant que la taille des échantillons est suffisamment grande.

Si l’hypothèse de normalité est gravement violée, vous avez deux choix :

1. Transformez les valeurs de réponse de vos données afin que les distributions soient distribuées plus normalement.

2. Effectuez un test non paramétrique équivalent tel que le test de Friedman qui ne nécessite pas l’hypothèse de normalité.

Hypothèse 3 : Sphéricité

Une ANOVA à mesures répétées suppose la sphéricité – c’est-à-dire que les variances des différences entre toutes les combinaisons de groupes apparentés doivent être égales.

Si cette hypothèse n’est pas respectée, le rapport F devient gonflé et les résultats des mesures répétées de l’ANOVA deviennent peu fiables.

Comment déterminer si cette hypothèse est remplie

Pour tester si cette hypothèse est remplie, nous pouvons effectuer le test de sphéricité de Mauchly .

Ce test utilise l’hypothèse nulle et alternative suivante :

• H ₀ : Les variances des différences sont égales
• H _A : Les variances des différences ne sont pas égales

Si la valeur p du test est inférieure à un certain niveau de signification (par exemple α = 0,05), alors nous rejetons l’hypothèse nulle et concluons que les variances des différences ne sont pas égales.

Sinon, si la valeur p n’est pas inférieure à un certain niveau de signification (par exemple α = 0,05), nous ne parvenons pas à rejeter l’hypothèse nulle et concluons que l’hypothèse de sphéricité est remplie.

Selon le logiciel statistique que vous utilisez, les résultats de ce test ressembleront à ceci :

Puisque la valeur p n’est pas inférieure à 0,05, nous ne parviendrons pas à rejeter l’hypothèse nulle et à conclure que l’hypothèse de sphéricité est remplie dans cet exemple particulier.

Que faire si cette hypothèse n’est pas respectée

Si nous rejetons l’hypothèse nulle du test de sphéricité de Mauchly, nous appliquons généralement une correction aux degrés de liberté utilisés pour calculer la valeur F dans le tableau ANOVA à mesures répétées.

Il y a trois corrections que nous pouvons appliquer :

• Huynh-Feldt (le moins conservateur)
• Serre–Geisser
• Limite inférieure (la plus conservatrice)

Chacune de ces corrections a tendance à augmenter les valeurs p dans le tableau de sortie de l’ANOVA à mesures répétées pour tenir compte du fait que l’hypothèse de sphéricité est violée.

Nous pouvons ensuite utiliser ces valeurs p pour déterminer si nous devons rejeter ou non l’hypothèse nulle de l’ANOVA à mesures répétées.

Ressources additionnelles

Les didacticiels suivants fournissent des informations supplémentaires sur l’ANOVA à mesures répétées :

Une introduction à l’ANOVA à mesures répétées
Calculateur ANOVA à mesures répétées
Comment rapporter les résultats d’une ANOVA à mesures répétées
ANOVA unidirectionnelle et ANOVA à mesures répétées : la différence