Comment effectuer une mise à l’échelle multidimensionnelle en Python
En statistiques, la mise à l’échelle multidimensionnelle est un moyen de visualiser la similarité des observations dans un ensemble de données dans un espace cartésien abstrait (généralement un espace 2D).
Le moyen le plus simple d’effectuer une mise à l’échelle multidimensionnelle en Python consiste à utiliser la fonction MDS() du sous-module sklearn.manifold .
L’exemple suivant montre comment utiliser cette fonction dans la pratique.
Exemple : mise à l’échelle multidimensionnelle en Python
Supposons que nous ayons le DataFrame pandas suivant qui contient des informations sur divers joueurs de basket-ball :
import pandas as pd #create DataFrane df = pd.DataFrame({'player': ['A', 'B', 'C', 'D', 'E', 'F', 'G', 'H', 'I', 'J', 'K'], 'points': [4, 4, 6, 7, 8, 14, 16, 19, 25, 25, 28], 'assists': [3, 2, 2, 5, 4, 8, 7, 6, 8, 10, 11], 'blocks': [7, 3, 6, 7, 5, 8, 8, 4, 2, 2, 1], 'rebounds': [4, 5, 5, 6, 5, 8, 10, 4, 3, 2, 2]}) #set player column as index column df = df.set_index('player') #view Dataframe print(df) points assists blocks rebounds player A 4 3 7 4 B 4 2 3 5 C 6 2 6 5 D 7 5 7 6 E 8 4 5 5 F 14 8 8 8 G 16 7 8 10 H 19 6 4 4 I 25 8 2 3 J 25 10 2 2 K 28 11 1 2
Nous pouvons utiliser le code suivant pour effectuer une mise à l’échelle multidimensionnelle avec la fonction MDS() du module sklearn.manifold :
from sklearn.manifold import MDS
#perform multi-dimensional scaling
mds = MDS(random_state=0)
scaled_df = mds.fit_transform(df)
#view results of multi-dimensional scaling
print(scaled_df)
[[ 7.43654469 8.10247222]
[ 4.13193821 10.27360901]
[ 5.20534681 7.46919526]
[ 6.22323046 4.45148627]
[ 3.74110999 5.25591459]
[ 3.69073384 -2.88017811]
[ 3.89092087 -5.19100988]
[ -3.68593169 -3.0821144 ]
[ -9.13631889 -6.81016012]
[ -8.97898385 -8.50414387]
[-12.51859044 -9.08507097]]
Chaque ligne du DataFrame d’origine a été réduite à une coordonnée (x, y).
Nous pouvons utiliser le code suivant pour visualiser ces coordonnées dans un espace 2D :
import matplotlib.pyplot as plt #create scatterplot plt.scatter(scaled_df[:,0], scaled_df[:,1]) #add axis labels plt.xlabel('Coordinate 1') plt.ylabel('Coordinate 2') #add lables to each point for i, txt in enumerate(df.index): plt.annotate(txt, (scaled_df[:,0][i]+.3, scaled_df[:,1][i])) #display scatterplot plt.show()
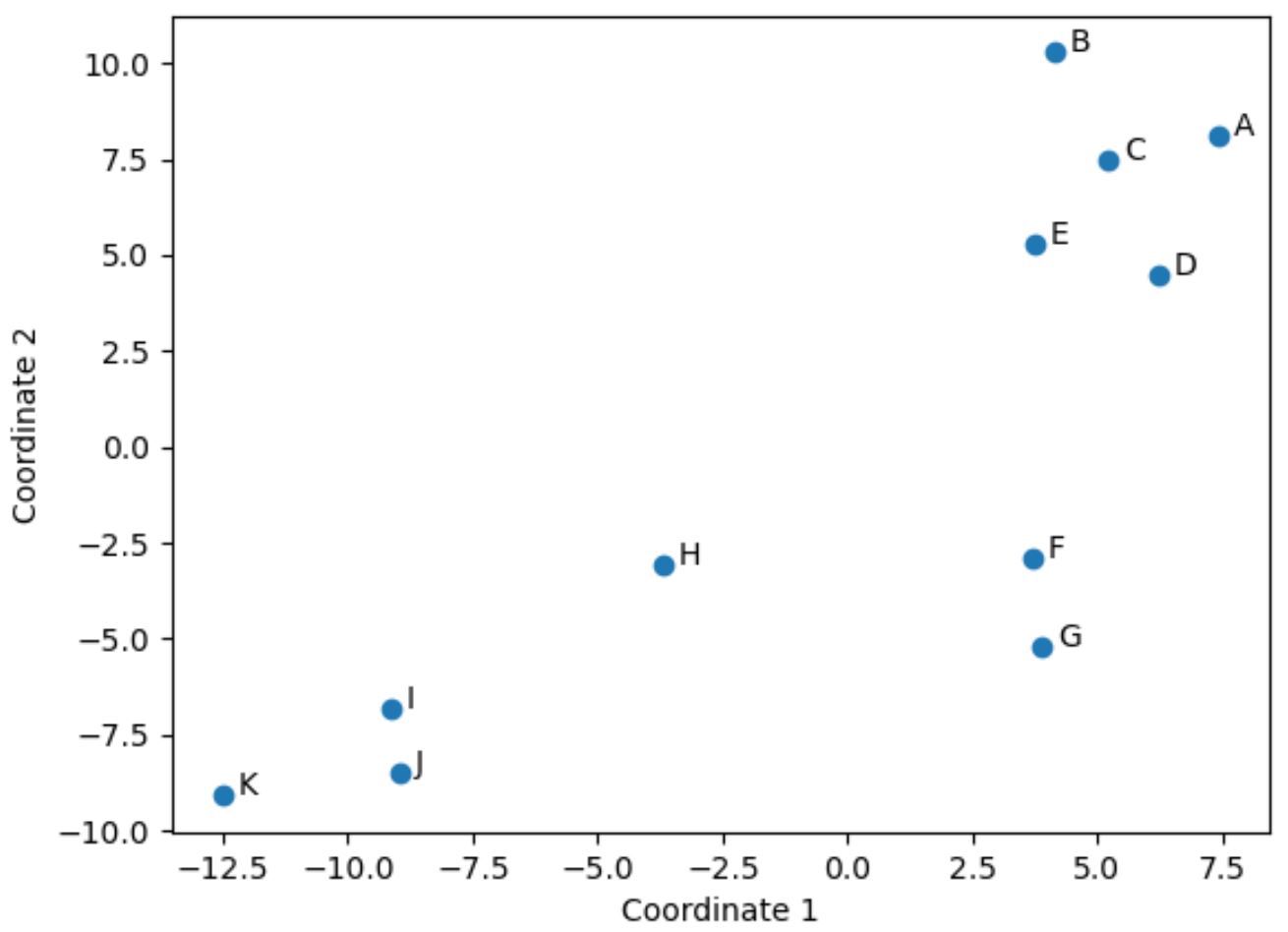
Les joueurs du DataFrame d’origine qui ont des valeurs similaires dans les quatre colonnes d’origine (points, passes décisives, blocages et rebonds) sont proches les uns des autres dans l’intrigue.
Par exemple, les joueurs F et G sont proches l’un de l’autre. Voici leurs valeurs du DataFrame d’origine :
#select rows with index labels 'F' and 'G'
df.loc[['F', 'G']]
points assists blocks rebounds
player
F 14 8 8 8
G 16 7 8 10
Leurs valeurs pour les points, les passes décisives, les blocages et les rebonds sont toutes assez similaires, ce qui explique pourquoi ils sont si proches les uns des autres dans le tracé 2D.
En revanche, considérons les joueurs B et K qui sont éloignés l’un de l’autre dans l’intrigue.
Si nous nous référons à leurs valeurs dans le DataFrame d’origine, nous pouvons voir qu’elles sont assez différentes :
#select rows with index labels 'B' and 'K'
df.loc[['B', 'K']]
points assists blocks rebounds
player
B 4 2 3 5
K 28 11 1 2
Ainsi, le tracé 2D est un bon moyen de visualiser à quel point chaque joueur est similaire à travers toutes les variables du DataFframe.
Les joueurs ayant des statistiques similaires sont regroupés à proximité tandis que les joueurs ayant des statistiques très différentes sont éloignés les uns des autres dans l’intrigue.
Ressources additionnelles
Les didacticiels suivants expliquent comment effectuer d’autres tâches courantes en Python :
Comment normaliser les données en Python
Comment supprimer les valeurs aberrantes en Python
Comment tester la normalité en Python
