MLE pour une distribution de Poisson (étape par étape)

L’estimation du maximum de vraisemblance (MLE) est une méthode qui peut être utilisée pour estimer les paramètres d’une distribution donnée.

Ce tutoriel explique comment calculer le MLE pour le paramètre λ d’une distribution de Poisson .

Étape 1 : Rédigez le PDF.

Tout d’abord, écrivez la fonction de densité de probabilité de la distribution de Poisson :

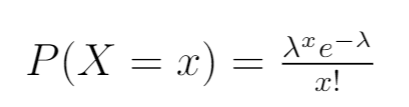
Étape 2 : Écrivez la fonction de vraisemblance.

Ensuite, écrivez la fonction de vraisemblance. Il s’agit simplement du produit de la PDF pour les valeurs observées x ₁ , …, x _n .

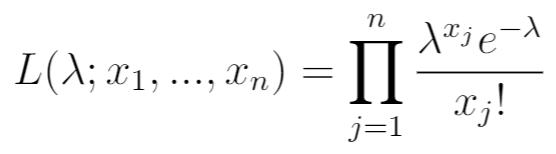
Étape 3 : Écrivez la fonction de vraisemblance du logarithme naturel.

Pour simplifier les calculs, nous pouvons écrire la fonction de vraisemblance naturelle :

Étape 4 : Calculez la dérivée de la fonction de vraisemblance naturelle par rapport à λ.

Ensuite, nous pouvons calculer la dérivée de la fonction de vraisemblance naturelle par rapport au paramètre λ :

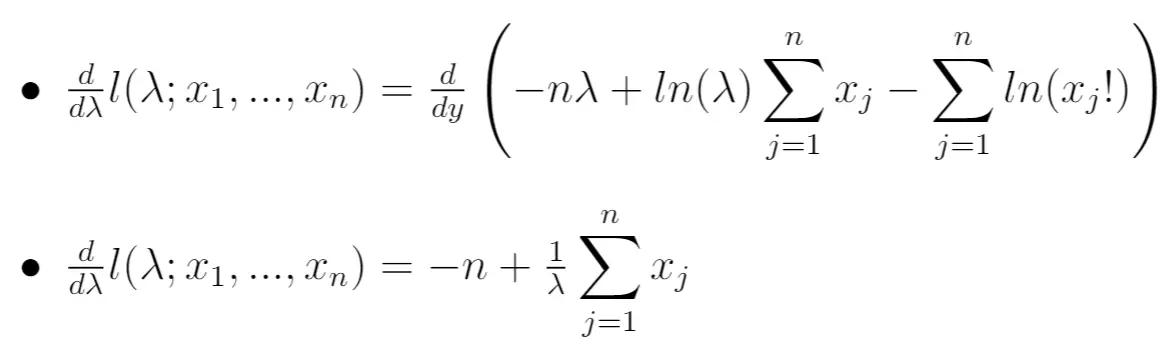
Étape 5 : Définissez la dérivée égale à zéro et résolvez λ.

Enfin, nous fixons la dérivée de l’étape précédente égale à zéro et résolvons simplement λ :

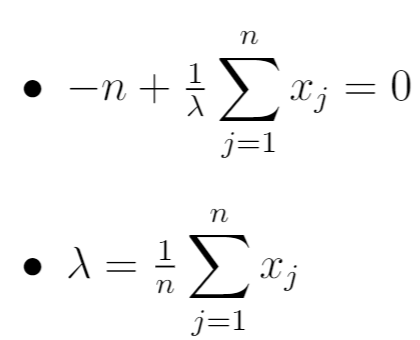
Ainsi, le MLE s’avère être :

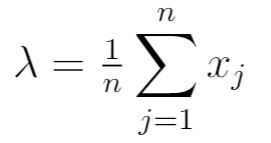
Cela équivaut à la moyenne de l’échantillon des n observations de l’échantillon.

Ressources additionnelles

Une introduction à la distribution de Poisson
Calculateur de distribution de Poisson
Comment utiliser la distribution de Poisson dans Excel