Moindres carrés

Par Pr Amélia Rodriguez août 2, 2023 Statistiques 0 commentaire

Cet article explique ce que sont les moindres carrés en statistique, ce qu’est la méthode des moindres carrés et comment un modèle de régression est ajusté par le critère des moindres carrés.

Quelle est la méthode des moindres carrés ?

La méthode des moindres carrés est une méthode statistique utilisée pour déterminer l’équation d’une régression. Autrement dit, la méthode des moindres carrés est un critère utilisé dans un modèle de régression pour minimiser l’erreur obtenue lors du calcul de l’équation de régression.

Concrètement, la méthode des moindres carrés consiste à minimiser la somme des carrés des résidus, ou en d’autres termes, elle repose sur la minimisation de la somme des carrés des différences entre les valeurs prédites par le modèle de régression et les valeurs observées. . Ci-dessous nous verrons en détail comment un modèle de régression est ajusté par le critère des moindres carrés.

La principale caractéristique de la méthode des moindres carrés est que les distances les plus longues entre les valeurs observées et la fonction de régression sont minimisées. Contrairement à d’autres critères de régression, la méthode des moindres carrés considère qu’il est plus important de minimiser les grands résidus que les petits résidus, puisque le carré d’un grand nombre est beaucoup plus grand que le carré d’un petit nombre.

Erreur d’estimation

Pour bien comprendre le concept des moindres carrés, nous devons d’abord savoir clairement ce que sont les résidus dans un modèle de régression. Nous verrons donc ci-dessous ce qu’est une erreur d’estimation et comment elle est calculée.

En statistique, l’ erreur d’estimation , également appelée résiduel , est la différence entre la vraie valeur et la valeur ajustée par le modèle de régression. Un résidu statistique est donc calculé comme suit :

$e_i=y_i-\widehat{y}_i$

Où:

$e_i$ est le résidu des données i.
$y_i$ est la valeur réelle des données i.
$\widehat{y}_i$ est la valeur fournie par le modèle de régression pour les données i.

Ainsi, plus le résidu d’une donnée est grand, plus le modèle de régression est mal adapté à cette donnée. Ainsi, plus un résidu est petit, plus la distance entre sa valeur réelle et sa valeur prédite est petite.

De même, si le résidu d’une donnée est positif, cela signifie que le modèle de régression a prédit une valeur inférieure à la valeur réelle. Alors que si le résidu est négatif, cela signifie que la valeur prédite est supérieure à la valeur réelle.

Minimiser les carrés des erreurs

Maintenant que nous savons ce qu’est un résidu en statistique, il sera plus facile de comprendre comment les carrés des erreurs sont minimisés.

Le carré d’une erreur est le carré d’un résidu, donc le carré d’une erreur est égal à la différence entre la vraie valeur et la valeur ajustée par le modèle de régression élevée à la puissance deux.

$e_i^2=(y_i-\widehat{y}_i)^2$

Où:

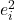$e_i^2$ est le carré du résiduel des données i.
$y_i$ est la valeur réelle des données i.
$\widehat{y}_i$ est la valeur fournie par le modèle de régression pour les données i.

Ainsi, la méthode des moindres carrés consiste à réaliser un modèle de régression en minimisant la somme des carrés des erreurs . Le critère des moindres carrés repose donc sur la minimisation de l’expression suivante :

$\begin{array}{l} [MIN] \ \displaystyle \sum_{i=1}^ne_i^2\\[4ex][MIN] \ \displaystyle \sum_{i=1}^n(y_i-\widehat{y}_i)^2\end{array}$

C’est pourquoi le critère des moindres carrés est également appelé critère des moindres carrés.

Comme vous pouvez le voir dans la formule précédente, le critère des moindres carrés donne plus d’importance à minimiser les gros résidus que les petits résidus. Par exemple, si un résidu vaut 3 et un autre résidu vaut 5, leurs carrés valent respectivement 9 et 25, donc le critère des moindres carrés donnera la priorité à la minimisation du deuxième résidu avant le premier résidu.

Ajustement par moindres carrés

L’ajustement d’un modèle de régression par le critère des moindres carrés consiste à trouver un modèle de régression qui minimise les carrés des résidus. Par conséquent, l’équation obtenue à partir du modèle de régression sera celle dont les carrés des différences entre les valeurs observées et les valeurs ajustées sont minimes.

Notez dans l’exemple suivant qu’il existe plus de critères pour créer un modèle de régression et, selon le critère choisi, l’équation de régression est différente.

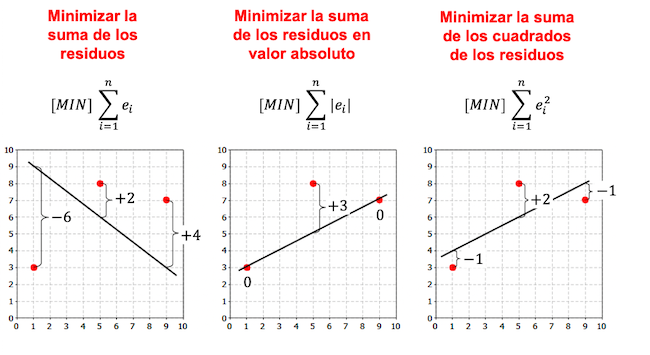
méthode des moindres carrés, ajustement des moindres carrés

Comme vous pouvez le voir dans les exemples précédents, la droite obtenue à partir du modèle de régression linéaire pour le même ensemble de données dépend du critère choisi. Généralement, le critère des moindres carrés est utilisé dans les modèles de régression.

En statistique, le modèle de régression le plus utilisé est le modèle de régression linéaire simple, qui consiste à approximer la relation entre la variable indépendante X et la variable dépendante Y à l’aide d’une droite.

$y=b_0+b_1x$

Ainsi, les formules pour ajuster un ensemble de données à un modèle de régression linéaire simple sont les suivantes :

$b_1=\cfrac{\displaystyle \sum_{i=1}^n (x_i-\overline{x})(y_i-\overline{y})}{\displaystyle \sum_{i=1}^n (x_i-\overline{x})^2}$

$b_0=\overline{y}-b_1\overline{x}$

Vous pouvez voir un exemple de la façon dont un modèle de régression linéaire simple est calculé selon le critère des moindres carrés en cliquant sur le lien suivant :

➤ Voir : Exemple de régression linéaire simple

à propos de l'auteur

Pr Amélia Rodriguez

En mettant l'accent sur l'apprentissage interactif et les applications pratiques, la professeure Amélia Rodriguez propose des tutoriels complets et des exemples concrets pour rendre les concepts de probabilité accessibles et pertinents pour la vie de ses étudiants. Lire plus