Moindres carrés partiels en Python (étape par étape)
L’un des problèmes les plus courants que vous rencontrerez en apprentissage automatique est la multicolinéarité . Cela se produit lorsque deux variables prédictives ou plus dans un ensemble de données sont fortement corrélées.
Lorsque cela se produit, un modèle peut être capable de bien s’adapter à un ensemble de données d’entraînement, mais il peut avoir des performances médiocres sur un nouvel ensemble de données qu’il n’a jamais vu, car il surajuste l’ensemble d’entraînement.
Une façon de contourner ce problème consiste à utiliser une méthode appelée moindres carrés partiels , qui fonctionne comme suit :
- Standardisez les variables prédictives et de réponse.
- Calculez M combinaisons linéaires (appelées « composantes PLS ») des p variables prédictives d’origine qui expliquent une quantité significative de variation à la fois de la variable de réponse et des variables prédictives.
- Utilisez la méthode des moindres carrés pour ajuster un modèle de régression linéaire en utilisant les composants PLS comme prédicteurs.
- Utilisez la validation croisée k-fold pour trouver le nombre optimal de composants PLS à conserver dans le modèle.
Ce didacticiel fournit un exemple étape par étape de la façon d’effectuer des moindres carrés partiels en Python.
Étape 1 : Importer les packages nécessaires
Tout d’abord, nous allons importer les packages nécessaires pour effectuer les moindres carrés partiels en Python :
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.preprocessing import scale
from sklearn import model_selection
from sklearn.model_selection import RepeatedKFold
from sklearn.model_selection import train_test_split
from sklearn.cross_decomposition import PLSRegression
from sklearn.metrics import mean_squared_error
Étape 2 : Charger les données
Pour cet exemple, nous utiliserons un ensemble de données appelé mtcars , qui contient des informations sur 33 voitures différentes. Nous utiliserons hp comme variable de réponse et les variables suivantes comme prédicteurs :
- mpg
- afficher
- merde
- poids
- qsec
Le code suivant montre comment charger et afficher cet ensemble de données :
#define URL where data is located
url = "https://raw.githubusercontent.com/Statology/Python-Guides/main/mtcars.csv"
#read in data
data_full = pd.read_csv(url)
#select subset of data
data = data_full[["mpg", "disp", "drat", "wt", "qsec", "hp"]]
#view first six rows of data
data[0:6]
mpg disp drat wt qsec hp
0 21.0 160.0 3.90 2.620 16.46 110
1 21.0 160.0 3.90 2.875 17.02 110
2 22.8 108.0 3.85 2.320 18.61 93
3 21.4 258.0 3.08 3.215 19.44 110
4 18.7 360.0 3.15 3.440 17.02 175
5 18.1 225.0 2.76 3.460 20.22 105
Étape 3 : Ajuster le modèle des moindres carrés partiels
Le code suivant montre comment adapter le modèle PLS à ces données.
Notez que cv = RepeatedKFold() indique à Python d’utiliser la validation croisée k-fold pour évaluer les performances du modèle. Pour cet exemple nous choisissons k = 10 plis, répété 3 fois.
#define predictor and response variables
X = data[["mpg", "disp", "drat", "wt", "qsec"]]
y = data[["hp"]]
#define cross-validation method
cv = RepeatedKFold(n_splits=10, n_repeats=3, random_state=1)
mse = []
n = len(X)
# Calculate MSE with only the intercept
score = -1*model_selection.cross_val_score(PLSRegression(n_components=1),
np.ones((n,1)), y, cv=cv, scoring='neg_mean_squared_error').mean()
mse.append(score)
# Calculate MSE using cross-validation, adding one component at a time
for i in np.arange(1, 6):
pls = PLSRegression(n_components=i)
score = -1*model_selection.cross_val_score(pls, scale(X), y, cv=cv,
scoring='neg_mean_squared_error').mean()
mse.append(score)
#plot test MSE vs. number of components
plt.plot(mse)
plt.xlabel('Number of PLS Components')
plt.ylabel('MSE')
plt.title('hp')
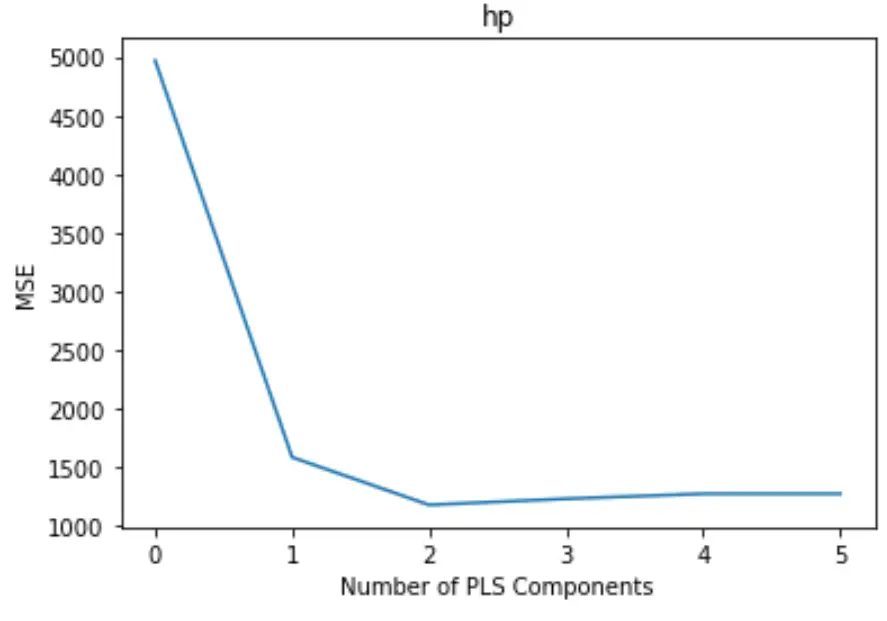
Le tracé affiche le nombre de composants PLS le long de l’axe des x et le test MSE (erreur quadratique moyenne) le long de l’axe des y.
À partir du graphique, nous pouvons voir que le MSE du test diminue en ajoutant deux composants PLS, mais il commence à augmenter à mesure que nous ajoutons plus de deux composants PLS.
Ainsi, le modèle optimal inclut uniquement les deux premières composantes PLS.
Étape 4 : Utiliser le modèle final pour faire des prédictions
Nous pouvons utiliser le modèle PLS final avec deux composants PLS pour faire des prédictions sur de nouvelles observations.
Le code suivant montre comment diviser l’ensemble de données d’origine en un ensemble de formation et de test et utiliser le modèle PLS avec deux composants PLS pour faire des prédictions sur l’ensemble de test.
#split the dataset into training (70%) and testing (30%) sets
X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=0.3,random_state=0)
#calculate RMSE
pls = PLSRegression(n_components=2)
pls.fit(scale(X_train), y_train)
np.sqrt(mean_squared_error(y_test, pls.predict(scale(X_test))))
29.9094
On voit que le RMSE du test s’avère être 29.9094 . Il s’agit de l’écart moyen entre la valeur prédite de hp et la valeur observée de hp pour les observations de l’ensemble de tests.
Le code Python complet utilisé dans cet exemple peut être trouvé ici .