Qu’est-ce que le Moi de Moran ? (Définition & #038; Exemple)

Le I de Moran est un moyen de mesurer l’autocorrélation spatiale.

En termes simples, il s’agit d’un moyen de quantifier à quel point les valeurs sont regroupées dans un espace 2D. Il est souvent utilisé en géographie et en science de l’information géographique (SIG) pour mesurer le degré de regroupement de différentes entités sur une carte, comme le revenu du ménage, le niveau d’éducation, etc.

Moran’s I : la formule

La formule pour calculer le I de Moran est :

I = (N/W)*ΣΣw _ij (x _i – x )(x _j – x )/Σ(x _i – x ) ²

où:

• N : Le nombre d’unités spatiales indexées par i et j
• W : La somme de tous les w _ij
• x : La variable d’intérêt (revenu du ménage, années de scolarité, etc.)
• x : La moyenne de x
• w _ij : Une matrice de poids spatiaux

Vous n’aurez probablement jamais à calculer cette mesure à la main puisque la plupart des logiciels statistiques peuvent la calculer pour vous, mais il est utile de connaître la formule utilisée sous le capot.

La valeur du I de Moran peut aller de -1 à 1 où :

• -1 : La variable d’intérêt est parfaitement dispersée
• 0 : la variable d’intérêt est dispersée de manière aléatoire
• 1 : La variable d’intérêt est parfaitement regroupée

Parallèlement au calcul du I de Moran, la plupart des logiciels statistiques calculent une valeur p correspondante qui peut être utilisée pour déterminer si les données sont dispersées de manière aléatoire ou non.

Le test de Moran utilise les hypothèses nulles et alternatives suivantes :

Hypothèse nulle (H ₀ ) : les données sont dispersées de manière aléatoire.

Hypothèse alternative (H _A ) : les données ne sont pas dispersées de manière aléatoire, c’est-à-dire qu’elles sont regroupées selon des modèles visibles.

Si la valeur p qui correspond au I de Moran est inférieure à un certain niveau de signification (c’est-à-dire α = 0,05), alors nous pouvons rejeter l’hypothèse nulle et conclure que les données sont regroupées spatialement de telle manière qu’il est peu probable qu’elles soient regroupées dans l’espace. sont survenus par hasard.

Moran’s I : quelques exemples

Les exemples suivants représentent de fausses cartes avec des valeurs différentes pour le I de Moran.

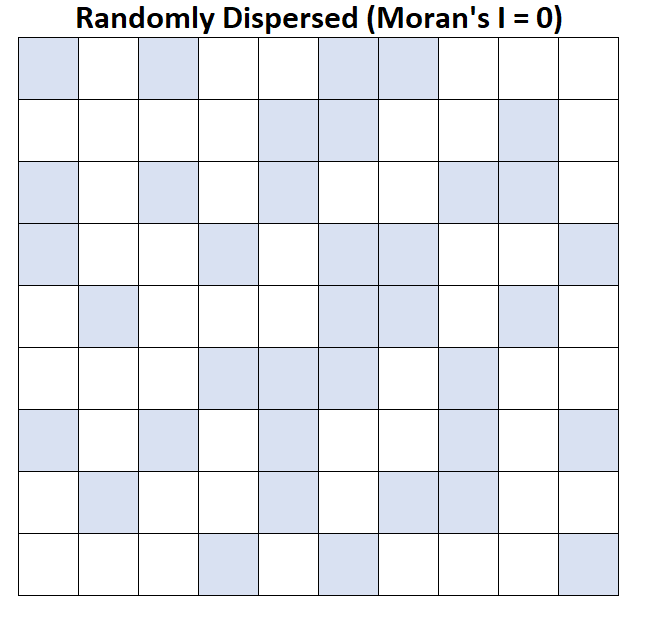
Supposons que chaque carré de la carte représente un comté et que les comtés dont le revenu moyen des ménages est supérieur à 50 000 $ sont indiqués en bleu.

I de Moran = 0 : le revenu moyen du ménage est dispersé de manière aléatoire (c’est-à-dire des grappes aléatoires dans des zones aléatoires).

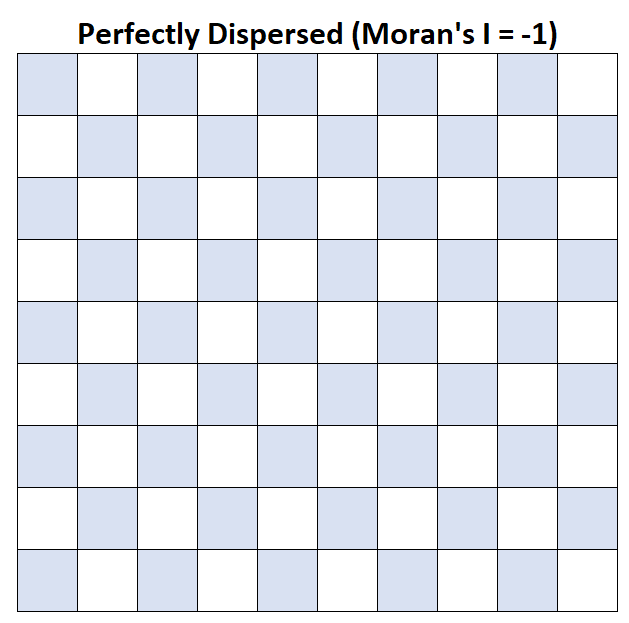
I de Moran = -1 : Le revenu moyen du ménage est parfaitement dispersé.

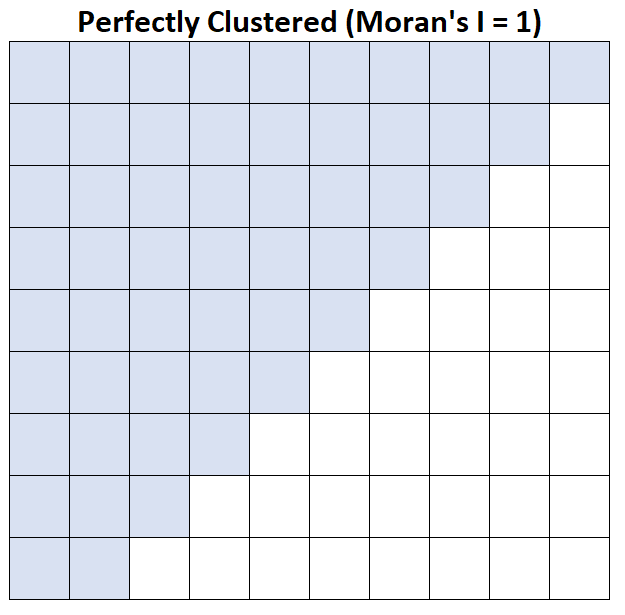
I de Moran = 1 : le revenu moyen du ménage est parfaitement regroupé.

Reportez-vous à cet exemple pour un exemple concret de calcul du I de Moran dans le logiciel statistique R.