Moyenne arithmétique

Par Pr Amélia Rodriguez août 6, 2023 Statistiques 0 commentaire

Nous expliquons ici ce qu’est la moyenne arithmétique et comment elle est calculée. Vous trouverez des exemples de moyenne arithmétique et même une calculatrice pour trouver la moyenne arithmétique de n’importe quel échantillon statistique. Enfin, vous pourrez voir quelles sont les propriétés de ce type de moyenne et comment la moyenne arithmétique est obtenue avec des données regroupées en intervalles.

Quelle est la moyenne arithmétique ?

La moyenne arithmétique est une valeur centrale caractéristique d’un ensemble de données statistiques. Pour calculer la moyenne arithmétique, toutes les valeurs sont additionnées et divisées par le nombre total de données.

Par ailleurs, la moyenne arithmétique est l’un des principaux indicateurs utilisés pour réaliser une étude statistique d’un échantillon.

La formule de la moyenne arithmétique est donc la suivante :

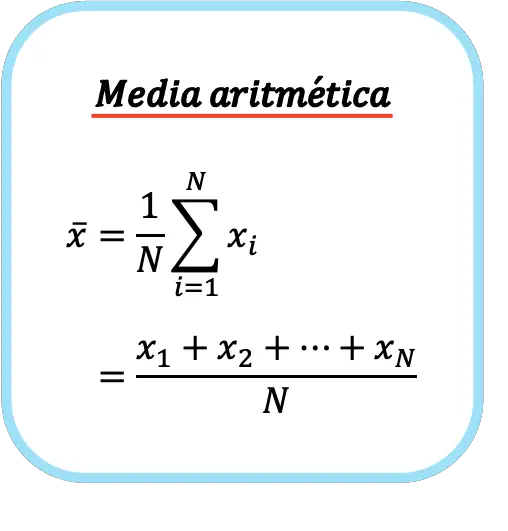
Le symbole de la moyenne arithmétique est une bande horizontale au-dessus de la lettre x.

$(\overline{x}).$ Vous pouvez également différencier la moyenne de l’échantillon de la moyenne de la population avec le symbole de moyenne : la moyenne d’un échantillon est exprimée avec le symbole $\overline{x}$ , par contre, pour la moyenne d’une population, on utilise la lettre grecque $\mu.$

Il convient de noter que la moyenne arithmétique d’une population équivaut à la valeur attendue de la variable statistique.

La moyenne arithmétique, également appelée moyenne arithmétique, n’est pas le seul type de moyenne qui existe, il existe également la moyenne pondérée, la moyenne carrée, la moyenne géométrique et la moyenne harmonique, entre autres. Vous pouvez voir comment chacun d’eux est calculé dans le moteur de recherche de notre site Web.

Comment calculer la moyenne arithmétique

Pour calculer la moyenne arithmétique, les étapes suivantes doivent être effectuées :

Ajoutez toutes les données statistiques de l’échantillon.
Divisez la somme précédente par le nombre total de données.
Le résultat obtenu est la moyenne arithmétique de l’échantillon statistique.

👉 Vous pouvez utiliser la calculatrice ci-dessous pour calculer la moyenne arithmétique de n’importe quel ensemble de données.

Exemple de calcul de la moyenne arithmétique

Étant donné la définition de la moyenne arithmétique, nous allons voir comment obtenir la moyenne arithmétique d’un ensemble de données en résolvant un exemple étape par étape.

Un élève a obtenu les notes suivantes au cours d’une année scolaire : en mathématiques un 9, en langue un 7, en histoire un 6, en économie un 8 et en sciences un 7,5. Quelle est la moyenne arithmétique de toutes vos notes ?

Pour trouver la moyenne arithmétique, nous devons additionner toutes les notes, puis diviser par le nombre total de matières du cours, qui est 5. Par conséquent, nous appliquons la formule de la moyenne arithmétique :

$\displaystyle\overline{x}=\frac{1}{N}\sum_{i=1}^N x_i=\frac{x_1+x_2+x_3+x_4+x_5}{N}$

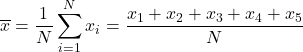
Nous substituons les données dans la formule et calculons la moyenne arithmétique :

$\overline{x}=\cfrac{9+7+5+8+7,5}{5}=7,3$

Comme vous pouvez le constater, dans la moyenne arithmétique, le même poids est attribué à chaque valeur, c’est-à-dire que chaque donnée a le même poids au sein de l’ensemble.

Calculateur de moyenne arithmétique

Entrez les données de n’importe quel échantillon statistique dans la calculatrice suivante pour calculer sa moyenne arithmétique. Les données doivent être séparées par un espace et saisies en utilisant le point comme séparateur décimal.

Moyenne arithmétique pour les données groupées

Par données groupées, nous entendons que les données sont structurées sous forme de groupes ou d’intervalles. Cela se produit généralement lorsque la taille de l’échantillon statistique est très grande.

Ainsi, le calcul de la moyenne arithmétique varie un peu lorsque les données sont regroupées, même si le concept est le même.

Pour calculer la moyenne arithmétique des données regroupées en intervalles, la note de classe de chaque groupe doit être multipliée par sa fréquence absolue, puis divisée par la somme de toutes les fréquences absolues.

$\displaystyle\overline{x}=\frac{\sum_{i=1}^N x_i\cdot f_i}{\sum_{i=1}^N f_i} =\frac{x_1\cdot f_1+ x_2\cdot f_2+\dots +x_N\cdot f_N}{N}$

Remarque : La note de classe d’un intervalle se calcule en divisant la somme des extrémités de l’intervalle par deux. Par exemple, la note de classe de l’intervalle [3,7) serait :

$\cfrac{3+7}{2}=5$

Pour que vous puissiez voir comment cela se fait, vous avez ci-dessous un exercice résolu sur la moyenne arithmétique de données regroupées en intervalles :

Nous souhaitons étudier statistiquement le poids d’un groupe, pour cela nous avons interrogé un groupe représentatif de 81 personnes et nous avons obtenu les données suivantes :

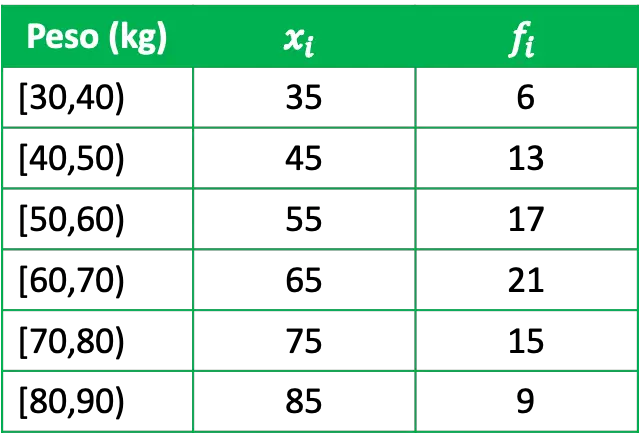
Où x _i est la note de classe de chaque groupe et f _i sa fréquence absolue, c’est-à-dire le nombre de personnes qui ont un poids dans cet intervalle.

Afin de déterminer la moyenne arithmétique, il faut ajouter une colonne dans le tableau des fréquences qui est le produit des notes de classe par leurs fréquences absolues respectives :

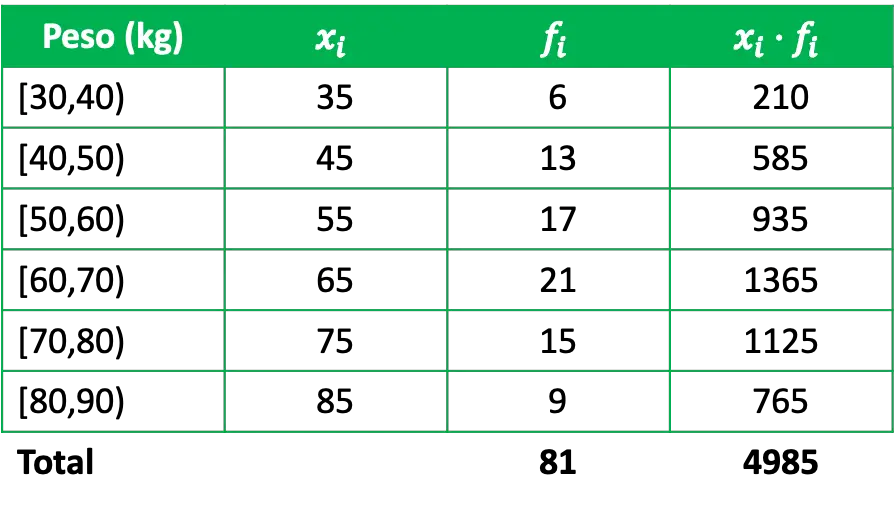
exercice de moyenne arithmétique résolue pour des données groupées

Ainsi, pour calculer la moyenne arithmétique des données regroupées, il suffit de diviser la somme des produits des notes de classe par leurs fréquences par le nombre total de données :

$\displaystyle\overline{x}=\frac{\sum_{i=1}^N x_i\cdot f_i}{\sum_{i=1}^N f_i} =\frac{4985}{81}=61,54 \text{ kg}$

Propriétés de la moyenne arithmétique

La moyenne arithmétique présente les caractéristiques suivantes :

La somme des écarts de toutes les données d’une distribution par rapport à la moyenne donne zéro.

$\sum_{i=1}^N\left(x_i-\overline{x}\right)=0$

Si nous ajoutons la même quantité à toutes les données d’un échantillon, la moyenne de l’échantillon augmente de ce montant.

La même chose se produit avec la multiplication, si l’on multiplie toutes les valeurs d’un échantillon par un nombre, la moyenne de l’échantillon est multipliée par ce nombre.

La moyenne arithmétique ne peut être calculée qu’en variables quantitatives . Autrement dit, vous ne pouvez pas prendre la moyenne de variables qualitatives.

La moyenne arithmétique sera toujours une valeur comprise entre le minimum et le maximum d’une distribution.

$\text{min}\{x_1,x_2,...,x_N\}\leq \cfrac{x_1+\dots +x_N}{N}\leq \text{max}\{x_1,x_2,...,x_N\}$

Ce type de moyenne est très sensible aux valeurs très élevées ou très faibles, ce qui fait qu’une valeur aberrante modifie considérablement le résultat de la moyenne arithmétique.

La moyenne arithmétique d’un ensemble de données est toujours égale ou supérieure à la moyenne géométrique du même ensemble de données.

$\displaystyle\frac{x_1+x_2+\dots+x_N}{N}\geq \sqrt[N]{x_1+x_2+\dots+x_N}$

Calculer la moyenne arithmétique avec Excel

Calculer la moyenne arithmétique dans Excel est très simple, puisqu’il suffit de saisir les données sur une feuille et d’utiliser la fonction MOYENNE .

Par exemple, pour déterminer la moyenne arithmétique des données du premier exercice résolu que nous avons expliqué, il suffit de copier toutes les données dans un document Excel et d’écrire la formule suivante dans une cellule : =MOYENNE(9;7;5 ;8;7 ,5) . La fonction renverra la moyenne arithmétique des données, qui est de 7,3.

Évidemment, il est beaucoup plus rapide de trouver la moyenne arithmétique de certains nombres avec le programme Excel que de la calculer à la main, surtout lorsque la taille de l’échantillon est très grande.

à propos de l'auteur

Pr Amélia Rodriguez

En mettant l'accent sur l'apprentissage interactif et les applications pratiques, la professeure Amélia Rodriguez propose des tutoriels complets et des exemples concrets pour rendre les concepts de probabilité accessibles et pertinents pour la vie de ses étudiants. Lire plus