Moyenne de l’échantillon

Par Pr Amélia Rodriguez août 3, 2023 Statistiques 0 commentaire

Dans cet article, vous découvrirez quelle est la moyenne de l’échantillon dans les statistiques. De même, vous trouverez comment calculer la moyenne d’un échantillon, un exercice résolu et, en plus, un calculateur en ligne pour calculer la moyenne de n’importe quel échantillon.

Quelle est la moyenne de l’échantillon ?

En statistiques, la moyenne de l’échantillon est la moyenne des valeurs d’un échantillon. Pour calculer la moyenne de l’échantillon, toutes les valeurs de l’échantillon doivent être additionnées puis divisées par le nombre total de données de l’échantillon.

Le symbole de la moyenne de l’échantillon est

$\overline{x}$ .

Dans une étude statistique, généralement toutes les valeurs d’une population ne sont pas connues, c’est pourquoi un échantillon de la population est sélectionné pour l’analyser et extrapoler les conclusions obtenues à l’ensemble de la population. Ainsi, la moyenne de l’échantillon est utilisée pour estimer la moyenne de la population.

Exemple de formule moyenne

La moyenne de l’échantillon est égale à la somme de toutes les valeurs de l’échantillon divisée par la taille de l’échantillon. Autrement dit, pour calculer la moyenne de l’échantillon, toutes les valeurs de l’échantillon sont additionnées puis divisées par le nombre total de données de l’échantillon.

Par conséquent, la formule pour calculer la moyenne de l’échantillon est la suivante :

$\displaystyle\overline{x}=\frac{\displaystyle \sum_{i=1}^n x_i}{n}=\frac{x_1+x_2+\dots +x_n}{n}$

👉 Vous pouvez utiliser la calculatrice ci-dessous pour calculer la moyenne d’échantillon de n’importe quel ensemble de données.

Gardez à l’esprit que la moyenne de l’échantillon est calculée à l’aide des données d’un échantillon, de sorte que la valeur de la moyenne de la population peut différer de la valeur calculée.

Exemple de calcul de la moyenne de l’échantillon

Maintenant que nous connaissons la définition de la moyenne de l’échantillon et quelle est sa formule, voyons comment obtenir la moyenne de l’échantillon à partir d’un ensemble de données en résolvant un exemple simple.

José souhaite déménager au centre-ville, mais il n’a pas beaucoup de temps et ne peut donc pas analyser le prix de tous les appartements à louer. Vous décidez donc de regarder uniquement le prix de location de cinq appartements (indiqué ci-dessous) pour savoir combien il vous en coûtera pour vivre au centre-ville. Quelle est la moyenne des prix de l’échantillon ?

600 € 430 € 820 € 575 € 950 €

Pour trouver la moyenne de l’échantillon, nous devons additionner toutes les valeurs de l’échantillon, puis diviser par le nombre total d’observations, qui est 5. Ainsi, nous appliquons la formule de la moyenne de l’échantillon :

$\displaystyle\overline{x}=\frac{\displaystyle\sum_{i=1}^n x_i}{n}=\frac{x_1+x_2+x_3+x_4+x_5}{n}$

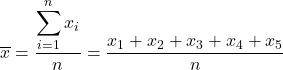
Ensuite, nous substituons les données dans la formule et calculons la moyenne de l’échantillon :

$\overline{x}=\cfrac{600+430+820+575+950}{5}=675$

En bref, le prix moyen de l’échantillon des appartements retenus pour l’échantillon est de 675 €.

Exemple de calculateur de moyenne

Entrez les données de n’importe quel échantillon statistique dans la calculatrice suivante pour calculer sa moyenne d’échantillon. Les données doivent être séparées par un espace et saisies en utilisant le point comme séparateur décimal.

Moyenne de l’échantillon et moyenne de la population

La moyenne de la population est la moyenne de la population statistique . La moyenne de population est donc la moyenne de tous les éléments sur lesquels une étude statistique est destinée à être réalisée.

Par conséquent, la différence entre la moyenne de l’échantillon et la moyenne de la population est que la moyenne de l’échantillon est la moyenne des valeurs de l’échantillon, tandis que la moyenne de la population est la moyenne des valeurs de la population.

Pour différencier la moyenne de l’échantillon de la moyenne de la population, elles sont représentées par des symboles différents. Le symbole de la moyenne de l’échantillon est

$\overline{x}$ , tandis que le symbole de la moyenne de la population est $\mu$ .

$\begin{array}{c}\overline{x} = \text{Media muestral}\\[2ex]\mu =\text{Media poblacional}\end{array}$

La moyenne de l’échantillon est utilisée pour estimer la valeur de la moyenne de la population, ce qui peut être effectué à l’aide d’une estimation ponctuelle ou d’une estimation par intervalle .

➤ Voir : Quelle est la moyenne de la population ?

Distribution d’échantillonnage de la moyenne de l’échantillon

Pour finir, voyons en quoi consiste la distribution d’échantillonnage de la moyenne de l’échantillon, car il s’agit d’un concept statistique qui peut créer de la confusion.

Tout d’abord, commençons par définir ce qu’est une distribution d’échantillonnage. Une distribution d’échantillonnage est la distribution qui résulte de la prise en compte de tous les échantillons possibles d’une population statistique.

Par conséquent, la distribution d’échantillonnage de la moyenne de l’échantillon est la distribution qui résulte du calcul de la moyenne de chaque échantillon possible d’une population. Autrement dit, si nous étudions tous les échantillons possibles d’une population et calculons la moyenne de chacun des échantillons, l’ensemble des valeurs calculées est une distribution d’échantillonnage de la moyenne de l’échantillon.

En conclusion, bien que la moyenne d’échantillon et la distribution d’échantillonnage portent des noms similaires, il faut savoir les distinguer : la moyenne d’échantillon est un paramètre statistique qui est calculé à partir d’un échantillon, en revanche, une distribution d’échantillonnage est une distribution qui résulte de l’étude de tous les échantillons qui peuvent être constitués à partir d’une population.

à propos de l'auteur

Pr Amélia Rodriguez

En mettant l'accent sur l'apprentissage interactif et les applications pratiques, la professeure Amélia Rodriguez propose des tutoriels complets et des exemples concrets pour rendre les concepts de probabilité accessibles et pertinents pour la vie de ses étudiants. Lire plus