Écart moyen absolu par rapport à l’écart type : quelle est la différence ?
L’ écart type est l’un des moyens les plus courants de mesurer la diffusion d’un ensemble de données.
Il est calculé comme suit :
Écart type = √( Σ(x je – x ) 2 / n )
Une autre façon de mesurer la répartition des observations dans un ensemble de données est l’ écart absolu moyen .
Il est calculé comme suit :
Déviation absolue moyenne = Σ|x i – x | /n
Ce didacticiel explique les différences entre ces deux métriques ainsi que des exemples de calcul de chacune.
Similitudes et différences
Comme leur nom l’indique, l’écart type et l’écart absolu moyen tentent de quantifier l’ écart typique des observations par rapport à la moyenne dans un ensemble de données donné.
Cependant, la méthode utilisée par chaque métrique est différente.
Écart-type
L’écart type trouve la différence au carré entre chaque observation et la moyenne d’un ensemble de données. Il fait ensuite la moyenne de ces carrés des différences et prend la racine carrée.
Cela nous laisse avec un nombre qui représente l’écart « standard » ou typique d’une observation par rapport à la moyenne.
Signifie une déviation absolue
À l’inverse, l’écart absolu moyen trouve l’ écart absolu entre chaque observation et la moyenne de l’ensemble de données. Il trouve ensuite la moyenne de ces écarts.
Cela nous laisse avec un nombre qui représente l’écart moyen des observations par rapport à la moyenne.
Étant donné que l’écart type trouve les différences au carré, il sera toujours égal ou supérieur à l’écart absolu moyen.
Lorsque des valeurs aberrantes extrêmes sont présentes, l’écart type sera considérablement plus grand que l’écart absolu moyen. L’exemple suivant illustre ce point.
Exemple : écart absolu moyen par rapport à l’écart type
Supposons que nous ayons l’ensemble de données suivant de 8 valeurs :
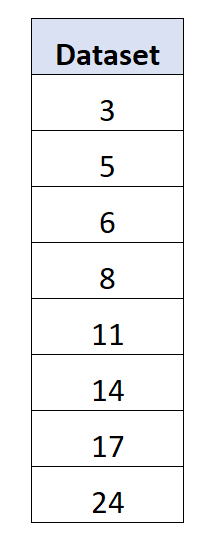
La moyenne s’avère être de 11 .
Ainsi, nous calculerions l’écart absolu moyen comme suit :
Déviation absolue moyenne = (|3-11| + |5-11| + |6-11| + |8-11| + |11-11| + |14-11| + |17-11| + |24- 11|) / 8 = 5,5 .
Et nous calculerions l’écart type comme suit :
Écart type = √((3-11) 2 + (5-11) 2 + (6-11) 2 + (8-11) 2 + (11-11) 2 + (14-11) 2 + (17- 11) 2 + (24-11) 2 ) / 8) = 6,595 .
Comme mentionné précédemment, l’écart type sera toujours égal ou supérieur à l’écart absolu moyen.
Cependant, la différence entre l’écart type et l’écart absolu moyen sera particulièrement importante s’il existe des valeurs aberrantes extrêmes dans l’ensemble de données.
Par exemple, considérons l’ensemble de données suivant avec une valeur aberrante extrême pour la dernière valeur :
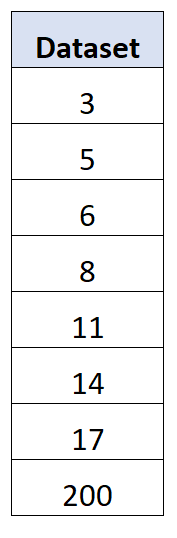
Il s’avère que l’écart type pour cet ensemble de données est de 63,27 tandis que l’écart absolu moyen est de 41,75 .
La valeur aberrante extrême fait que l’écart type est beaucoup plus grand que l’écart absolu moyen.
