Moyenne géométrique

Par Pr Amélia Rodriguez août 6, 2023 Statistiques 0 commentaire

Dans cet article, nous expliquons ce qu’est la moyenne géométrique, comment elle est calculée et quelle est la différence entre la moyenne géométrique et la moyenne arithmétique. Vous pourrez également voir un exercice résolu étape par étape de la moyenne géométrique et quelles sont les propriétés de ce type de moyenne. Enfin, vous trouverez une calculatrice pour calculer la moyenne géométrique de n’importe quel ensemble de données.

Quelle est la moyenne géométrique ?

La moyenne géométrique est une mesure de la position centrale des statistiques descriptives. La moyenne géométrique d’un ensemble de données statistiques est égale à la nième racine du produit de toutes les valeurs.

La moyenne géométrique est utilisée en finance d’entreprise pour calculer les taux de rendement, les moyennes en pourcentage et les intérêts composés.

La formule de la moyenne géométrique est donc la suivante :

La moyenne géométrique ne peut être calculée que lorsque toutes les données de l’échantillon sont positives. Parce que si une valeur est négative, la racine aurait une solution négative ou aucune solution, par contre, si une donnée est nulle alors la multiplication des données donnerait zéro et, par conséquent, la moyenne géométrique serait égale à 0.

La moyenne géométrique n’est pas le seul type de moyenne qui existe, il existe également la moyenne arithmétique, la moyenne pondérée, la moyenne quadratique et la moyenne harmonique.

Différence entre la moyenne géométrique et la moyenne arithmétique

La principale différence entre la moyenne géométrique et la moyenne arithmétique est que la moyenne géométrique est moins sensible aux valeurs extrêmes que la moyenne arithmétique. De plus, la moyenne arithmétique peut être calculée avec des valeurs négatives et nulles, alors que la moyenne géométrique ne peut être calculée qu’avec des valeurs positives.

De même, la moyenne géométrique sera en général inférieure à la moyenne arithmétique pour le même ensemble de données.

Il convient également de noter que le calcul de la moyenne géométrique est plus complexe et que, par conséquent, sa signification statistique est plus difficile à interpréter.

Bref, la moyenne géométrique présente des avantages et des inconvénients par rapport à la moyenne arithmétique et, selon la nature des données, il conviendra de calculer telle ou telle moyenne.

Comment calculer la moyenne géométrique

Pour calculer la moyenne géométrique, les étapes suivantes doivent être effectuées :

Calculez le produit de toutes les données statistiques de l’échantillon.
Trouvez la nième racine du produit calculé.
Le résultat obtenu est la moyenne géométrique de l’échantillon statistique.

Comme vous pouvez le constater, trouver la moyenne géométrique d’un ensemble de données est relativement simple avec une calculatrice ou un programme informatique, puisqu’il suffit de calculer un produit et une racine. Au contraire, il est assez laborieux de faire le calcul à la main.

👉 C’est pourquoi nous vous recommandons d’utiliser la calculatrice ci-dessous pour calculer la moyenne géométrique d’un ensemble de données.

Exemple de moyenne géométrique

Une fois que nous aurons vu la théorie sur la moyenne géométrique, nous allons faire un exemple afin que vous puissiez voir exactement comment obtenir la moyenne géométrique.

Les résultats économiques d’une entreprise des cinq dernières années sont connus. La première année, l’entreprise a généré une rentabilité économique de 10%, la deuxième année le bénéfice a atteint 23%, la troisième année l’argent gagné a été de 16%, la quatrième année elle a atteint une rentabilité économique de 7% et l’investissement de la cinquième année a représenté une rentabilité de 20%. Il vous est demandé de calculer la moyenne de tous les pourcentages.

Comme nous l’avons vu, pour calculer la moyenne des pourcentages, il ne faut pas utiliser la moyenne arithmétique, mais plutôt faire le calcul avec la moyenne géométrique.

Par conséquent, nous appliquons la formule de la moyenne géométrique :

$MG=\sqrt[n]{\prod_{i=1}^Nx_i}=\sqrt[n]{x_1\cdot x_2\cdot \ldots x_n}$

Et nous substituons les exemples de valeurs dans la formule et effectuons le calcul :

$MG=\sqrt[5]{1,10\cdot 1,23\cdot 1,16\cdot 1,07\cdot 1,20}=1,15 \ \longrightarrow \ 15 \%$

Notez que nous disposons de cinq points de données et que nous calculons donc la racine cinquième.

Le résultat numérique de la moyenne géométrique est 1,15, ce qui signifie que l’entreprise a connu une croissance économique de 15 % en moyenne chaque année.

Gardez à l’esprit que nous avons pu obtenir la moyenne géométrique car toutes les valeurs étaient positives, mais si un pourcentage avait été négatif, nous aurions dû mettre les données dans la formule sous la forme d’une décimale positive avec la partie entière. égal à zéro. Par exemple, une croissance de -30 % doit être exprimée dans la formule par 0,70 (1-0,3=0,7).

Calculateur de moyenne géométrique

Branchez n’importe quel échantillon de statistique dans la calculatrice ci-dessous pour trouver sa moyenne géométrique. Les données doivent être séparées par un espace et saisies en utilisant le point comme séparateur décimal. N’oubliez pas que vous ne pouvez pas déterminer la moyenne géométrique si une valeur est négative ou nulle.

Propriétés de la moyenne géométrique

La moyenne géométrique a les caractéristiques suivantes :

C’est un type de moyenne très utile pour trouver la moyenne de pourcentages ou d’indices.

Il ne peut être calculé que si toutes les données sont positives.

La signification géométrique de la moyenne géométrique de deux nombres a et b est le côté d’un carré de même aire que le rectangle dont les côtés mesurent a et b .

$MG(a,b)=\sqrt{a\cdot b}$

La signification géométrique de la moyenne géométrique de trois nombres a , b et c est le côté d’un cube dont le volume est équivalent au parallélépipède des côtés a , b et c .

$MG(a,b,c)=\sqrt[3]{a\cdot b \cdot c}$

Le logarithme de la moyenne géométrique d’un ensemble de données donne la moyenne arithmétique des logarithmes du même ensemble.

La moyenne géométrique d’un ensemble de valeurs sera toujours inférieure ou égale à la moyenne arithmétique.

$\sqrt[N]{x_1\cdot x_2\ldots x_N}\leq \cfrac{x_1+x_2+\ldots+x_N}{N}$

La moyenne géométrique pondérée est calculée de la même manière que la moyenne géométrique, mais en ajoutant des poids à l’exposant de chaque donnée pour pondérer les valeurs statistiques.

$\displaystyle \left(\prod_{i=1}^n{x_i}^{\alpha_i}\right)^{\frac{1}{\sum_i{\alpha_i}}}= \left({x_1}^{\alpha_1}{x_2}^{\alpha_2}\dots{x_n}^{\alpha_n}\right)^{ \frac{1}{\alpha_1+ \dots+ \alpha_n}} \left}}$

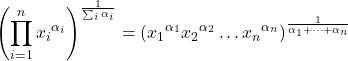
Calculer la moyenne géométrique dans Excel

Enfin, voyons comment trouver la moyenne géométrique d’un ensemble de données à l’aide du programme Excel.

Pour calculer la moyenne géométrique dans Excel, vous devez utiliser la fonction MEANS.GEOM. Il vous suffit de saisir toutes les valeurs dont vous souhaitez prendre la moyenne géométrique et la fonction renverra le résultat de la moyenne géométrique.

Par exemple, pour déterminer la moyenne géométrique de l’exemple travaillé ci-dessus, vous devez écrire dans une case Excel =MEDIA.GEOM(1.1;1.23;1.16;1.07;1.20) .

Vous devez garder à l’esprit que si l’une des valeurs est nulle ou négative, la fonction renverra une erreur.

Comme vous pouvez le constater, il est beaucoup plus simple et rapide de calculer une moyenne géométrique avec Excel, puisqu’il suffit de copier les données sur une feuille et d’utiliser une formule.

à propos de l'auteur

Pr Amélia Rodriguez

En mettant l'accent sur l'apprentissage interactif et les applications pratiques, la professeure Amélia Rodriguez propose des tutoriels complets et des exemples concrets pour rendre les concepts de probabilité accessibles et pertinents pour la vie de ses étudiants. Lire plus