Moyenne harmonique

Nous expliquons ici ce qu’est la moyenne harmonique et comment elle est calculée (formule). De plus, nous calculons la moyenne harmonique d’un exemple étape par étape. Vous trouverez également une calculatrice pour prendre la moyenne harmonique de n’importe quel ensemble de données. Et enfin, vous pourrez voir quelles sont les propriétés de la moyenne harmonique.

Quelle est la moyenne harmonique ?

La moyenne harmonique est une mesure de position centrale des statistiques descriptives. La moyenne harmonique est calculée en divisant le nombre total de données statistiques par la somme des inverses de chaque valeur.

La moyenne harmonique est utilisée pour calculer des moyennes de vitesses, de temps ou faire des calculs électroniques. Cette fonctionnalité différencie la moyenne harmonique des autres types de moyennes, fréquemment utilisés dans le calcul des prix moyens ou des pourcentages.

Ainsi, la formule de la moyenne harmonique est la suivante :

La moyenne harmonique est généralement représentée par un H majuscule.

Les autres types de moyenne qui existent sont la moyenne arithmétique, la moyenne pondérée, la moyenne carrée et la moyenne géométrique. La moyenne harmonique présente des avantages et des inconvénients par rapport aux autres types de moyenne, nous verrons ci-dessous de quoi il s’agit.

Comment calculer la moyenne harmonique

Pour calculer la moyenne harmonique, les étapes suivantes doivent être effectuées :

1. Calculez l’inverse de chaque donnée statistique de l’échantillon.
2. Ajoutez tous les inverses calculés.
3. Divisez le nombre total de données par la somme trouvée à l’étape précédente.
4. Le résultat obtenu est la moyenne harmonique de l’échantillon statistique.

👉 Comme vous pouvez le constater, prendre la moyenne harmonique d’un ensemble de données nécessite de nombreuses opérations, il est donc assez laborieux de le faire à la main. Par conséquent, pour calculer la moyenne harmonique, nous vous recommandons d’utiliser le calculateur ci-dessous.

Exemple de moyenne harmonique

Après avoir vu la théorie sur la moyenne harmonique, nous allons voir comment trouver la moyenne harmonique d’un ensemble de données en résolvant un exemple étape par étape du prix d’une action.

• Une personne achète des actions d’une entreprise chaque année pendant 5 années consécutives. Au cours de cette période, le prix des actions a beaucoup fluctué : la première année, chaque action valait 7 €, la deuxième année 10 €, la troisième année 15 €, la quatrième année, la société a connu d’importantes pertes financières et le prix est tombé à 6 € par action et, finalement, au cours de la cinquième année, l’entreprise a réalisé un investissement important qui a fait monter le prix à 11 €. Quel a été le prix moyen d’achat des actions ?

Une option consisterait à calculer la moyenne arithmétique, c’est-à-dire à additionner tous les prix et à les diviser par cinq. Cependant, comme les achats ont été effectués au cours d’années différentes, prendre la moyenne arithmétique serait une erreur. Il faut donc trouver la moyenne harmonique de tous les prix.

Ensuite, nous appliquons la formule de la moyenne harmonique :

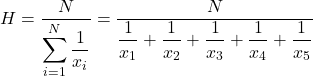
Et puis nous substituons les valeurs de prix problématiques dans la formule et calculons la moyenne harmonique :

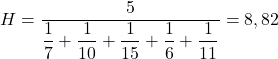
Il faut mettre cinq au numérateur de la fraction car il y a cinq informations différentes.

Ainsi, le prix moyen des actions que vous avez achetées durant cette période est de 8,82 euros par action.

Calculateur de moyenne harmonique

Avec la calculatrice suivante, vous pouvez calculer la moyenne harmonique de n’importe quel ensemble de données statistiques.

Vous devez saisir les nombres en utilisant le point comme séparateur décimal et séparer les nombres par un espace. N’oubliez pas que pour trouver la moyenne harmonique, aucune valeur ne peut être nulle.

Propriétés de la moyenne harmonique

La moyenne harmonique a les caractéristiques suivantes :

• Les valeurs élevées ont peu d’effet sur la moyenne harmonique d’un ensemble, c’est-à-dire qu’une valeur très grande par rapport aux autres données n’entraînera pas de changement notable dans la moyenne harmonique.

• En revanche, une petite valeur influence grandement la moyenne harmonique d’un ensemble, réduisant considérablement sa valeur. En effet, les réciproques du dénominateur de la formule prennent alors des valeurs très grandes.

• La moyenne harmonique ne peut pas être calculée si l’une des données est nulle, car cela entraînerait une indétermination dans la formule. Dans un tel cas, la moyenne harmonique est dite indéfinie.

• L’inverse de la moyenne harmonique équivaut à la moyenne arithmétique des inverses des observations.

• Pour un même groupe de données, la moyenne harmonique sera inférieure ou égale à la moyenne arithmétique.

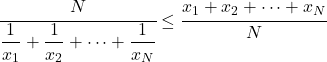
Calculer la moyenne harmonique avec Excel

Comme nous l’avons vu, calculer manuellement la moyenne harmonique peut s’avérer assez fastidieux car de nombreux calculs doivent être effectués. Et cela devient encore plus compliqué lorsque l’on dispose d’une grande quantité de données. C’est pourquoi, pour trouver la moyenne harmonique, nous recommandons d’utiliser une calculatrice ou le programme Excel.

La moyenne harmonique dans Excel est calculée avec la formule MEAN.ARMO . Autrement dit, pour calculer la moyenne harmonique d’un ensemble de données, vous devez les copier dans une feuille Excel et saisir toutes les données dans la fonction MEAN.ARMO .

Par exemple, pour obtenir la moyenne harmonique de l’exercice que nous avons résolu ci-dessus, vous écrivez dans une cellule Excel =MEDIA.ARMO(7;10;15;6;11) .

Vous devez garder à l’esprit que si l’une des valeurs est nulle, la fonction renverra une erreur, car la moyenne harmonique d’un ensemble de valeurs statistiques ne peut pas être déterminée si l’une d’entre elles est nulle.