Moyenne pondérée

Par Pr Amélia Rodriguez août 6, 2023 Statistiques 0 commentaire

Nous expliquons ici ce qu’est la moyenne pondérée et comment elle est calculée. Vous pourrez voir un exercice résolu sur la façon dont nous trouvons la moyenne pondérée. Et, en plus, vous pouvez calculer la moyenne pondérée de n’importe quel ensemble de données avec la calculatrice à la fin.

Quelle est la moyenne pondérée ?

La moyenne pondérée est une mesure de la position centrale des statistiques descriptives. Pour calculer la moyenne pondérée, il faut d’abord multiplier chaque donnée statistique par son poids (ou poids), puis additionner tous les produits, et enfin diviser la somme pondérée par la somme de tous les poids.

Autrement dit, la formule de la moyenne pondérée est la suivante :

Où x _i représente chaque échantillon de données et w _i son poids correspondant.

Ainsi, plus une donnée a un poids important, plus elle prend de l’importance dans le calcul de la moyenne pondérée. Autrement dit, plus la pondération d’une donnée est élevée, plus elle influencera le résultat de la moyenne pondérée.

La moyenne pondérée est particulièrement utile pour le calcul des notes, car elle permet d’évaluer avec une importance différente les exercices ou examens passés au cours d’un cours. La moyenne pondérée est également utilisée pour calculer l’IPC (Consumer Price Index), qui est un indicateur permettant de mesurer les prix d’une population.

Outre la moyenne pondérée, il existe également d’autres types de moyennes telles que la moyenne géométrique, la moyenne arithmétique, la moyenne quadratique et la moyenne harmonique.

Comment calculer la moyenne pondérée

Pour calculer la moyenne pondérée, les étapes suivantes doivent être suivies :

Multipliez chaque donnée statistique par son poids correspondant.
Additionnez tous les produits calculés à l’étape précédente.
Divisez la somme pondérée ci-dessus par la somme de tous les poids.
Le résultat obtenu est la moyenne pondérée de l’échantillon statistique.

👉 Vous pouvez utiliser la calculatrice ci-dessous pour calculer la moyenne pondérée de n’importe quel ensemble de données.

Exemple de moyenne pondérée

Compte tenu de la définition de la moyenne pondérée, nous allons maintenant résoudre un exercice pour bien comprendre comment la moyenne pondérée est obtenue à partir d’un ensemble de données.

Un élève de 1ère année d’un lycée a obtenu les notes suivantes dans la matière mathématiques : un 7 à l’examen partiel qui compte 30%, un 9 au travail de groupe qui vaut 20%, un 6 aux exercices dispensés en classe avec une pondération de 10 % et un 8 à l’examen final qui a une pondération de 40 %. Quelle est votre note finale pour la matière ?

Pour déterminer la note de l’élève, il faut trouver la moyenne pondérée avec les valeurs données par l’énoncé. Pour ce faire, nous appliquons la formule de moyenne pondérée :

$\overline{x_p}=\cfrac{\sum_{i=1}^N x_i\cdot w_i}{\sum_{i=1}^N w_i}=\cfrac{x_1\cdot w_1+x_2\cdot w_2+x_3\cdot w_3+x_4\cdot w_4+x_5\cdot w_5}{w_1+w_2+w_3+w_4+w_5}$

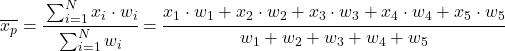
La note de chaque livrable est la valeur statistique et son pourcentage correspond au poids de ladite valeur. Par conséquent, nous substituons les valeurs et les poids dans la formule et effectuons le calcul de la moyenne pondérée :

$\overline{x_p}=\cfrac{7\cdot 0,30+9\cdot 0,20+6\cdot 0,10+8\cdot 0,40}{0,30+0,20+0,10+0,40}=7,7$

La note finale en mathématiques de cet élève sera donc de 7,7 car c’est le résultat obtenu à partir de la moyenne pondérée.

Calculateur de moyenne pondérée

Entrez les données de n’importe quel échantillon statistique et leurs poids respectifs dans la calculatrice ci-dessous pour calculer sa moyenne pondérée.

Inscrivez les données statistiques dans la première case et leurs poids respectifs dans la deuxième case. Vous devez écrire les poids dans le même ordre que les données et au format décimal. Tous les nombres doivent être séparés par un espace et saisis en utilisant le point comme séparateur décimal.

Poids normalisés

Comme nous l’avons vu, dans la moyenne pondérée, le poids est la valeur qui est donnée à chaque donnée pour lui donner plus ou moins d’importance. Ainsi, si une information est très importante, elle aura un poids très important, mais si une information n’est pas très pertinente, elle aura un poids très faible.

Eh bien, le poids normalisé est un type de pondération utilisé pour obtenir la moyenne pondérée sans avoir à faire de division.

Le poids normalisé est le poids d’un élément de données divisé par la somme de tous les poids.

$w_i'=\cfrac{w_i}{\sum_{k=1}^N w_k}$

La somme de tous les poids normalisés est donc égale à un :

$\sum_{i=1}^N w_i'=1$

Ainsi, pour calculer la moyenne pondérée avec les poids normalisés , multipliez simplement chaque élément de données par son poids normalisé :

$\displaystyle\overline{x_p}=\sum_{i=1}^N x_i\cdot w_i'=x_1\cdot w_1'+x_2\cdot w_2'+\dots+x_N\cdot w_N'$

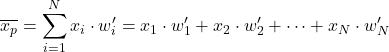
Par exemple, nous avons un échantillon statistique dont les données sont 24, 35, 17, 41 et leurs poids respectifs sont 4, 9, 6, 3. Pour trouver la moyenne pondérée de cet ensemble de données, nous pouvons d’abord calculer les poids normalisés en divisant chaque poids par la somme de tous les poids :

$\cfrac{4}{4+9+6+3}=0,18$

$\cfrac{9}{4+9+6+3}=0,41$

$\cfrac{6}{4+9+6+3}=0,27$

$\cfrac{3}{4+9+6+3}=0,14$

Et maintenant il suffit de multiplier chaque donnée par son poids normalisé et le résultat sera la moyenne pondérée :

$\overline{x_p}=24\cdot 0,18+35\cdot 0,41+17\cdot 0,27+41\cdot 0,14=28,91$

Différence entre la moyenne pondérée et la moyenne arithmétique

Le calcul de la moyenne pondérée et de la moyenne arithmétique se fait de la même manière, puisque des opérations similaires doivent être effectuées. Dans le calcul de la moyenne pondérée, chaque point de données est multiplié par son poids et divisé par la somme des poids, mais dans la moyenne arithmétique, toutes les données sont additionnées et divisées par le nombre total de points de données.

La différence entre la moyenne pondérée et la moyenne arithmétique réside dans son concept, puisque dans la moyenne arithmétique on considère que toutes les données ont la même valeur, cependant, dans la moyenne pondérée, chaque donnée a un poids différent.

Notez que si tous les poids sont égaux, la moyenne pondérée est équivalente à la moyenne arithmétique. Vous pouvez voir la preuve mathématique ci-dessous :

$\begin{aligned}\overline{x_p}&=\cfrac{x_1\cdot w+x_2\cdot w+x_3\cdot w+\dots+x_N\cdot w}{w+w+w+\dots +w}\\[2ex]&= \cfrac{w\cdot (x_1+x_2+\dots+x_N)}{N\cdot w}=\\[2ex] &= \cfrac{x_1+x_2+\dots+x_N}{N}=\overline{x}\end{aligned}$

à propos de l'auteur

Pr Amélia Rodriguez

En mettant l'accent sur l'apprentissage interactif et les applications pratiques, la professeure Amélia Rodriguez propose des tutoriels complets et des exemples concrets pour rendre les concepts de probabilité accessibles et pertinents pour la vie de ses étudiants. Lire plus