Comment calculer une moyenne tronquée dans Google Sheets

Une moyenne tronquée est la moyenne d’un ensemble de données qui a été calculée après avoir supprimé un pourcentage spécifique des valeurs les plus petites et les plus grandes de l’ensemble de données.

Par exemple, une moyenne tronquée de 10 % représenterait la moyenne d’un ensemble de données après la suppression des 10 % des valeurs des extrémités de l’ensemble de données.

Pour calculer une moyenne tronquée dans Google Sheets, vous pouvez utiliser la fonction TRIMMEAN , qui utilise la syntaxe de base suivante :

TRIMMEAN(données, exclure_proportion)

où:

• data : Plage contenant l’ensemble de données
• include_proportion : Proportion de données à exclure (entre 0 et 1)

L’exemple suivant montre comment utiliser cette fonction pour calculer une moyenne tronquée dans la pratique.

Exemple : calculer la moyenne tronquée dans Google Sheets

Supposons que nous ayons l’ensemble de données suivant dans Google Sheets :

Nous pouvons utiliser la formule suivante pour calculer une moyenne tronquée de 10 % pour cet ensemble de données :

TRIMMEAN(A2:A21, 0.1)

La capture d’écran suivante montre comment utiliser cette formule en pratique :

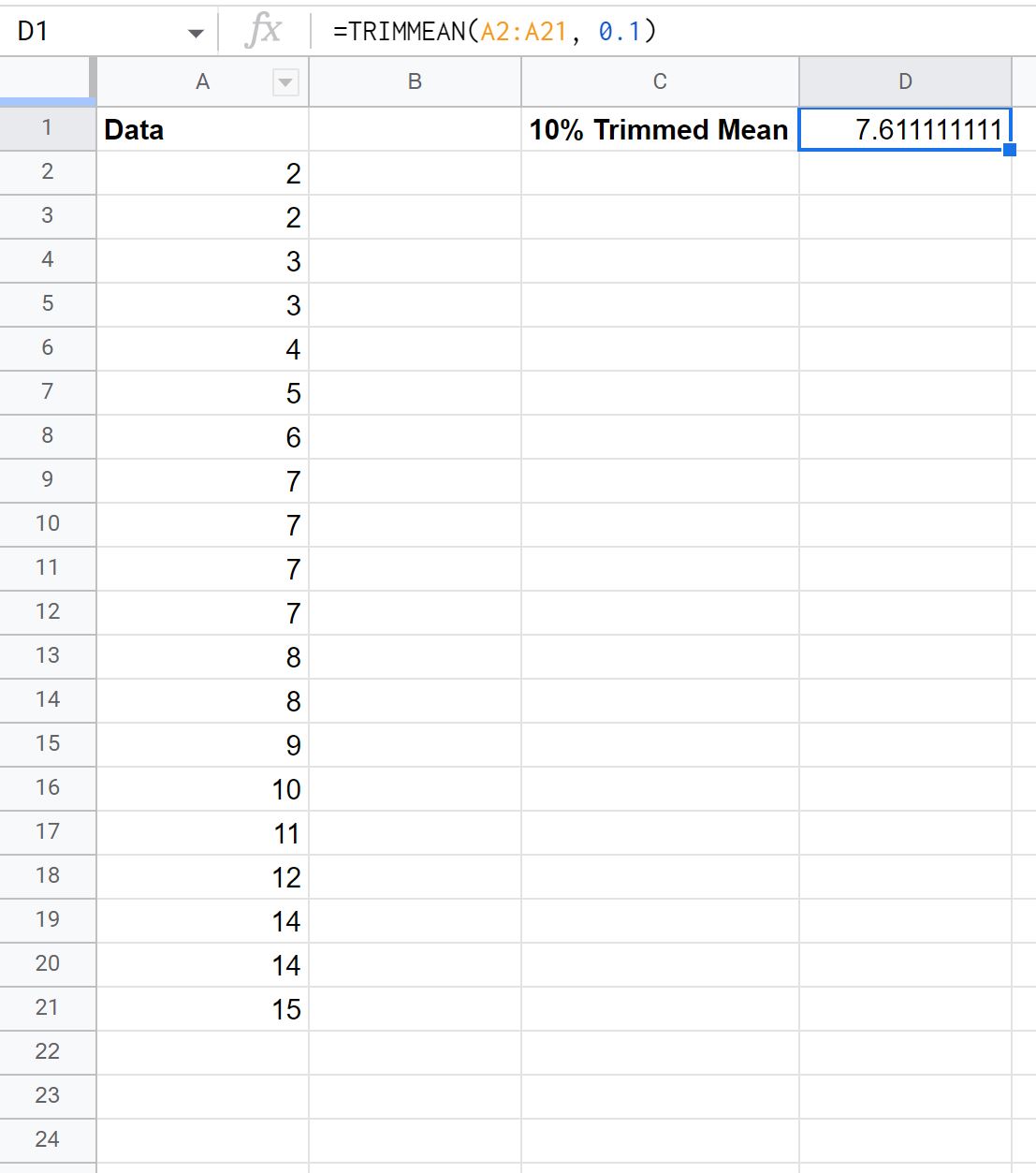
La moyenne tronquée à 10 % de l’ensemble de données est 7,61 .

Dans cet exemple particulier, il y a 20 valeurs totales dans l’ensemble de données. Ainsi, 10 % de 20 fait 2.

Ainsi, pour calculer une moyenne tronquée de 10 % dans cet exemple, Google Sheets doit supprimer deux valeurs des extrémités de l’ensemble de données.

Cela signifie que Google Sheets a supprimé la plus petite valeur (2) et la plus grande valeur (15) de l’ensemble de données, puis a calculé la moyenne.

Nous pouvons confirmer que la formule est correcte en calculant nous-mêmes manuellement cette moyenne tronquée :

Moyenne tronquée à 10 % : (2+3+3+4+5+6+7+7+7+7+8+8+9+10+11+12+14+14) / 18 = 7,61 .

Notez que dans cet exemple particulier, les valeurs supprimées des extrémités n’étaient clairement pas des valeurs aberrantes.

Cependant, une moyenne tronquée est plus utile en pratique lorsqu’il existe des valeurs aberrantes extrêmes dans l’ensemble de données et que vous souhaitez calculer la valeur moyenne sans permettre à ces valeurs aberrantes d’ influencer le calcul .

Ressources additionnelles

Les didacticiels suivants fournissent des informations supplémentaires sur les moyennes tronquées :

Comment calculer manuellement une moyenne tronquée
Comment calculer une moyenne tronquée en Python
Calculateur de moyenne tronquée