Événements mutuellement inclusifs ou mutuellement exclusifs

Deux événements s’excluent mutuellement s’ils ne peuvent pas se produire en même temps.

Par exemple, supposons que l’événement A soit l’événement selon lequel un dé tombe sur un nombre pair et que l’événement B soit l’événement selon lequel un dé tombe sur un nombre impair.

Nous définirions l’ espace échantillon pour les événements comme suit :

• UNE = {2, 4, 6}
• B = {1, 3, 5}

Notez qu’il n’y a pas de chevauchement entre les deux espaces échantillonnés. Ainsi, les événements A et B s’excluent mutuellement car ils ne peuvent pas se produire tous les deux en même temps. Le nombre sur lequel tombe un dé ne peut pas être à la fois pair et impair.

A l’inverse, deux événements s’inclusent mutuellement s’ils peuvent survenir en même temps.

Par exemple, soit l’événement C l’événement où un dé atterrit sur un nombre pair et soit l’événement D l’événement où un dé atterrit sur un nombre supérieur à 3.

Nous définirions l’espace échantillon pour les événements comme suit :

• C = {2, 4, 6}
• ré = {4, 5, 6}

Notez qu’il existe un chevauchement entre les deux espaces échantillonnés. Ainsi, les événements C et D s’inclusent mutuellement car ils peuvent tous deux se produire en même temps. Il est possible que les dés atterrissent sur un nombre pair et supérieur à 3.

Probabilités d’événements

Si deux événements s’excluent mutuellement , alors la probabilité qu’ils se produisent tous les deux est nulle.

Par exemple, considérons les deux exemples d’espaces pour les événements A et B précédents :

• UNE = {2, 4, 6}
• B = {1, 3, 5}

Puisqu’il n’y a pas de chevauchement dans les espaces d’échantillonnage, nous dirions P(A et B) = 0 .

Mais si deux événements sont mutuellement inclusifs , alors la probabilité qu’ils se produisent tous les deux sera un nombre supérieur à zéro.

Par exemple, considérons les deux exemples d’espaces pour les événements C et D précédemment :

• C = {2, 4, 6}
• ré = {4, 5, 6}

Puisqu’il y a 6 nombres possibles sur lesquels les dés pourraient atterrir et que deux de ces nombres (4 et 6) appartiennent aux deux événements C et D, nous calculerions P(C et D) comme 2/6, ou 1/3 .

Visualiser des événements mutuellement inclusifs et mutuellement exclusifs

Nous utilisons souvent des diagrammes de Venn pour visualiser les probabilités associées à des événements.

Si deux événements s’excluent mutuellement , ils ne se chevaucheront pas du tout dans un diagramme de Venn :

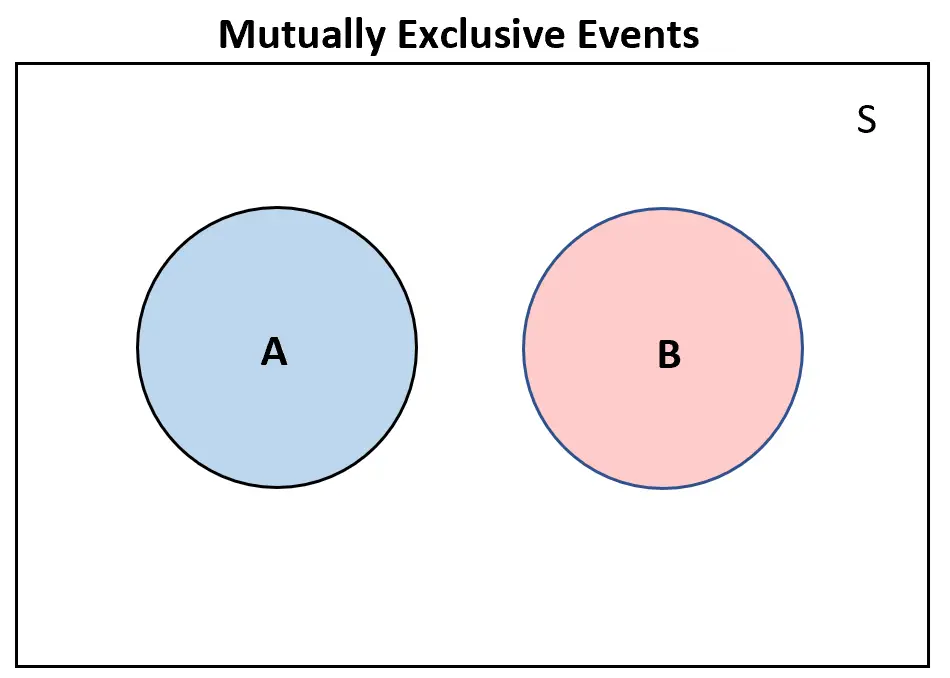
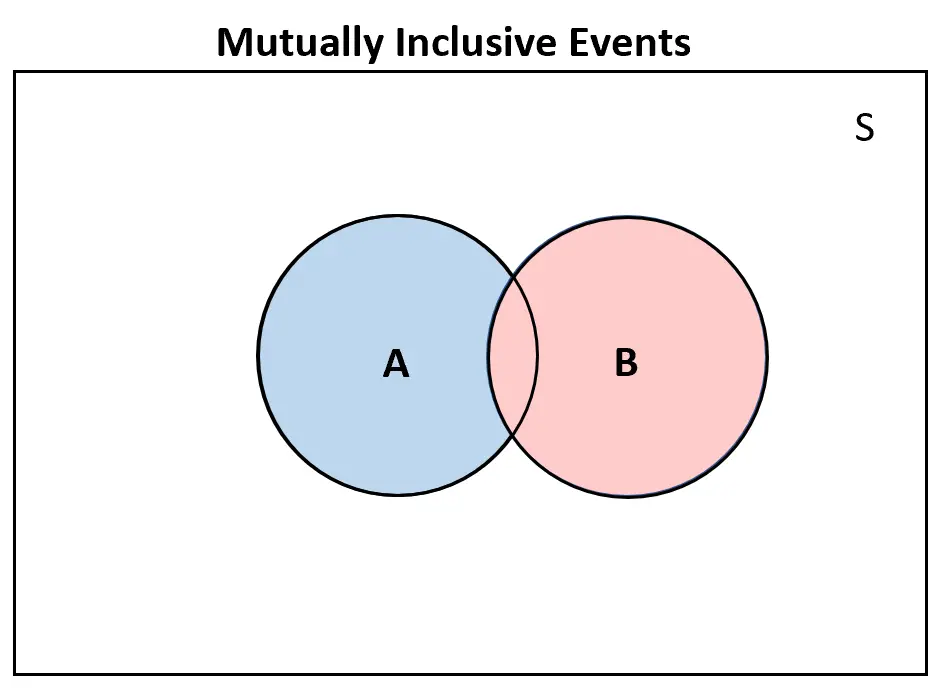
À l’inverse, si deux événements s’inclusent mutuellement , il y aurait au moins un certain chevauchement dans le diagramme de Venn :

Ressources additionnelles

Une introduction à la probabilité théorique
La règle générale de multiplication
Que sont les événements disjoints ?