Wat zijn dichtheidscurven? (uitleg & voorbeelden)

Een dichtheidscurve is een curve in een grafiek die de verdeling van waarden in een reeks gegevens weergeeft. Dit is om drie redenen nuttig:

1. Een dichtheidscurve geeft ons een goed beeld van de ‘vorm’ van een verdeling, inclusief of een verdeling al dan niet een of meer ‘pieken’ van frequentiewaarden heeft en of de verdeling al dan niet naar links scheef is of rechts. RECHTS. .

2. Met een dichtheidscurve kunnen we visueel zien waar het gemiddelde en de mediaan van een verdeling zich verhouden.

3. Met een dichtheidscurve kunnen we visueel zien welk percentage waarnemingen in een dataset tussen verschillende waarden ligt.

De meest bekende dichtheidscurve is de klokvormige curve die denormale verdeling weergeeft.

Om dichtheidscurven beter te begrijpen, kunt u het volgende voorbeeld overwegen.

Voorbeeld: een dichtheidscurve maken en interpreteren

Laten we zeggen dat we de volgende gegevensset hebben die de hoogte van 20 verschillende planten (in inches) in een bepaald veld toont:

4, 5, 5, 6, 6, 6, 6, 7, 7, 7, 7, 7, 8, 8, 8, 9, 9, 9, 2, 2

Als we een eenvoudig histogram zouden maken om de relatieve frequenties van elke waarde weer te geven, zou het er als volgt uitzien:

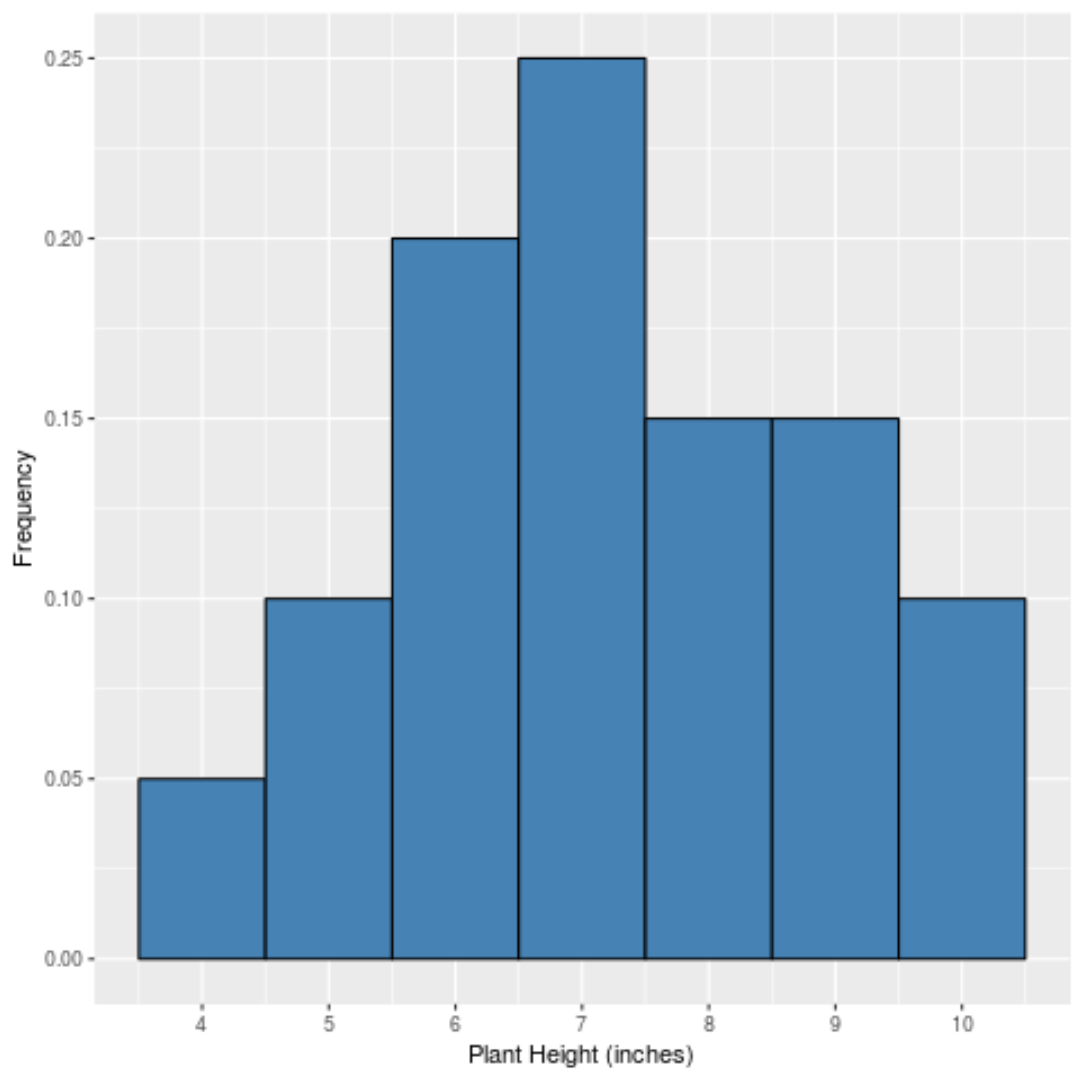
De x-as toont de gegevenswaarde en de y-as toont de relatieve frequentie (de waarde „7“ verschijnt bijvoorbeeld 5 keer van de 20 totale waarden in de dataset, dus deze heeft een relatieve frequentie van 25% of 0,25 .

En als we een dichtheidscurve zouden maken om de ‘vorm’ van deze verdeling vast te leggen, zou deze er als volgt uitzien:

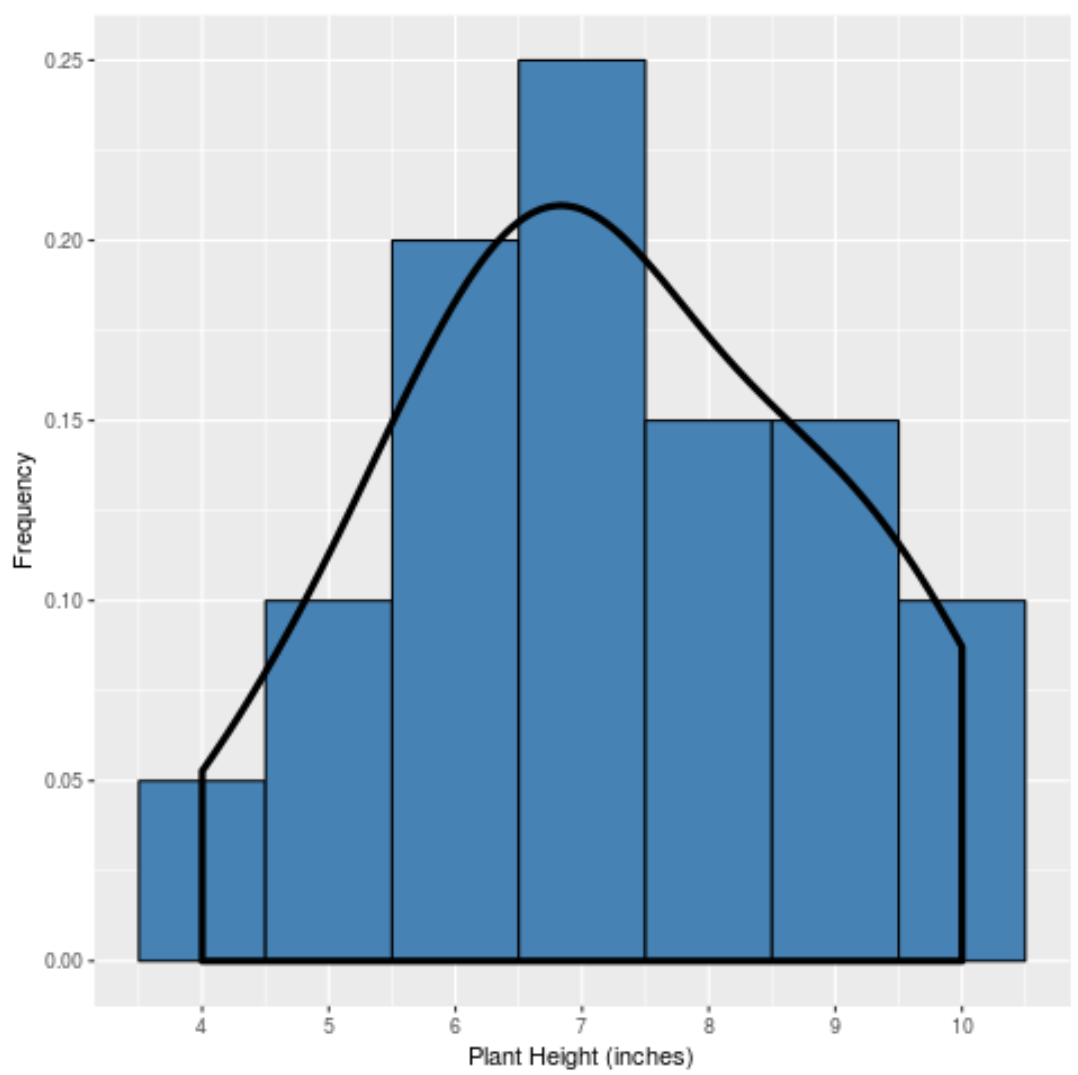
De curve is het hoogst nabij het midden van de verdeling, omdat daar de meeste waarden voorkomen. Het is ook het laagst nabij de uiteinden van de verdeling, omdat minder planten deze waarden aannemen (bijvoorbeeld een hoogte van 4 inch of 10 inch).

Hoe dichtheidscurven te interpreteren

Dichtheidscurven zijn er in alle soorten en maten en stellen ons in staat snel visueel inzicht te krijgen in de verdeling van waarden in een bepaalde dataset. Ze zijn vooral nuttig om ons te helpen visualiseren:

1. Asymmetrie

Scheefheid is een manier om de symmetrie van een verdeling te beschrijven. Met dichtheidscurven kunnen we snel zien of een grafiek naar links, rechts of helemaal niet gekanteld is:

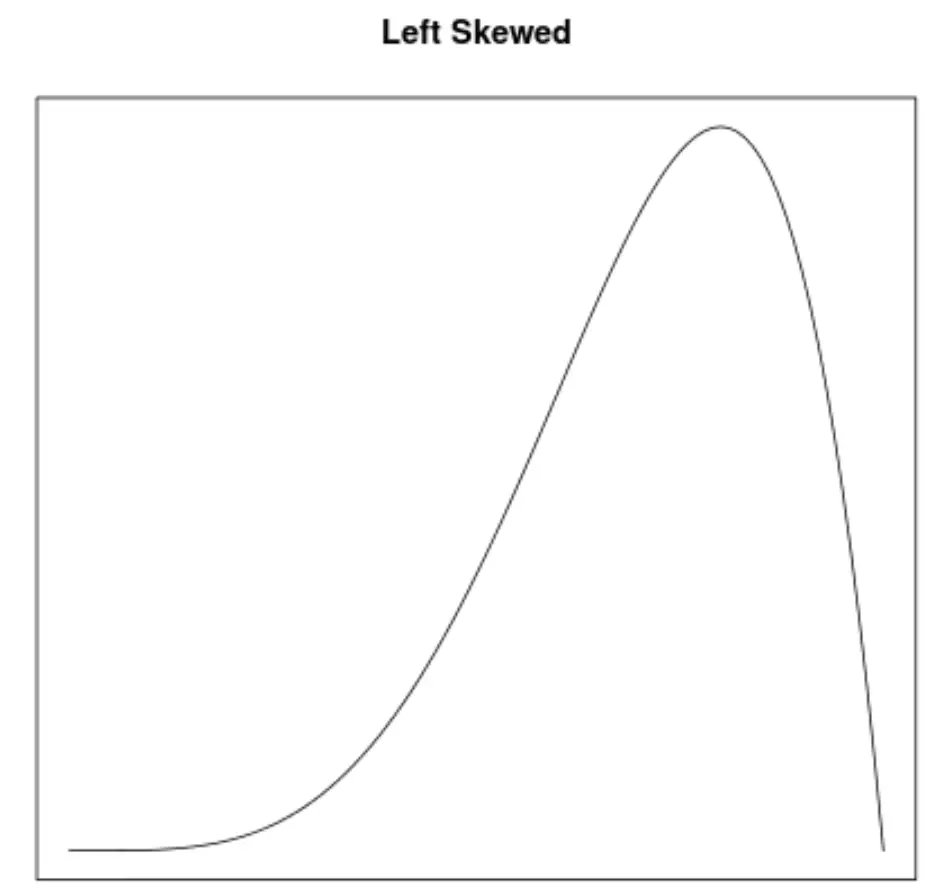
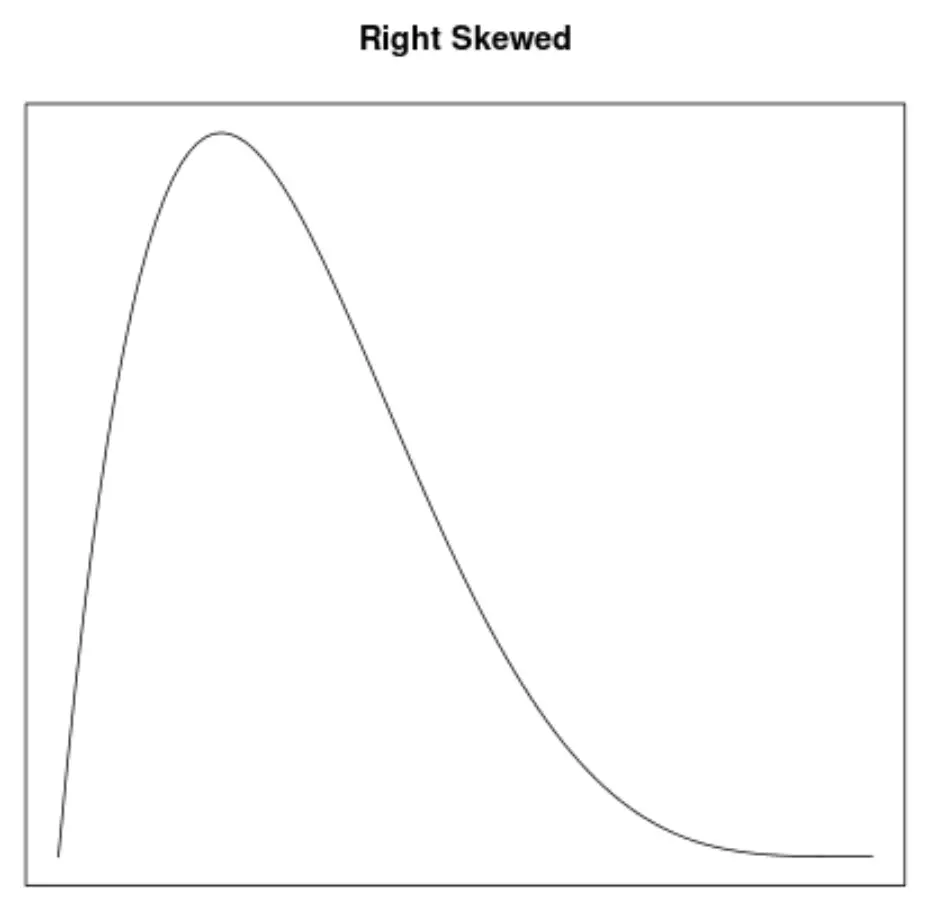
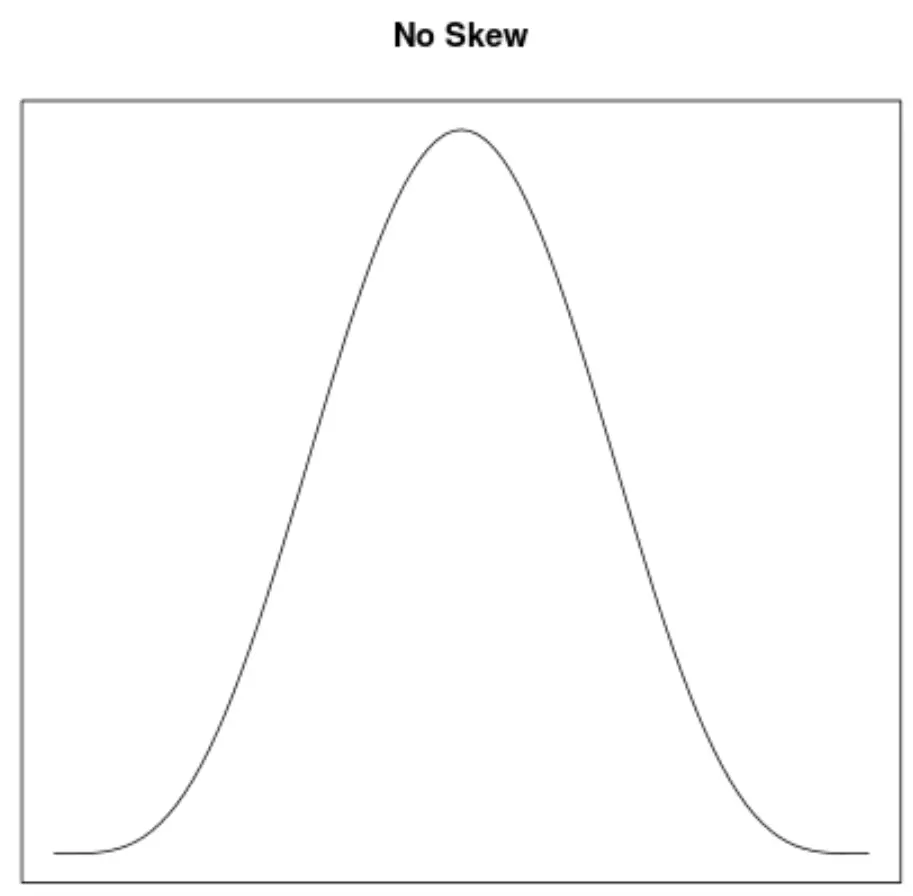
2. De locatie van het gemiddelde en de mediaan

Op basis van de scheefheid van een dichtheidscurve kunnen we snel zien of het gemiddelde of de mediaan groter is in een bepaalde verdeling. Speciaal:

• Als een dichtheidscurve asymmetrisch blijft , is het gemiddelde lager dan de mediaan.
• Als een dichtheidscurve naar rechts scheef is, is het gemiddelde groter dan de mediaan.
• Als een dichtheidscurve geen asymmetrie heeft, is het gemiddelde gelijk aan de mediaan.

3. Aantal pieken

Met dichtheidscurven kunnen we ook snel zien hoeveel ‘pieken’ er in een bepaalde verdeling zijn. In elk van de bovenstaande voorbeelden hadden de verdelingen slechts één piek, dus we zouden deze verdelingen als unimodaal omschrijven.

Sommige distributies kunnen echter twee pieken hebben, die webimodale distributies noemen. En in zeldzame gevallen kunnen we ook multimodale distributies hebben met twee of meer pieken.

Door simpelweg een dichtheidscurve te maken voor een bepaalde dataset, kunnen we snel zien hoeveel pieken er in de verdeling zitten.

Eigenschappen van dichtheidscurven

Dichtheidscurven hebben de volgende eigenschappen:

• De oppervlakte onder de curve bedraagt altijd 100%.
• De curve zal nooit onder de x-as komen.

Houd deze twee feiten in gedachten bij het maken of interpreteren van dichtheidscurven voor verschillende verdelingen.

Aanvullende bronnen

Inleiding tot relatieve frequentiehistogrammen
Hoe u een belcurve maakt in Excel
Hoe u een belcurve maakt in Python