Comment normaliser les données dans Excel

« Normaliser » un ensemble de valeurs de données signifie mettre les valeurs à l’échelle de telle sorte que la moyenne de toutes les valeurs soit 0 et l’écart type soit 1.

Ce tutoriel explique comment normaliser les données dans Excel.

Exemple : Comment normaliser les données dans Excel

Supposons que nous ayons l’ensemble de données suivant dans Excel :

Effectuez les étapes suivantes pour normaliser cet ensemble de valeurs de données.

Étape 1 : Trouvez la moyenne.

Tout d’abord, nous utiliserons la fonction =AVERAGE(plage de valeurs) pour trouver la moyenne de l’ensemble de données.

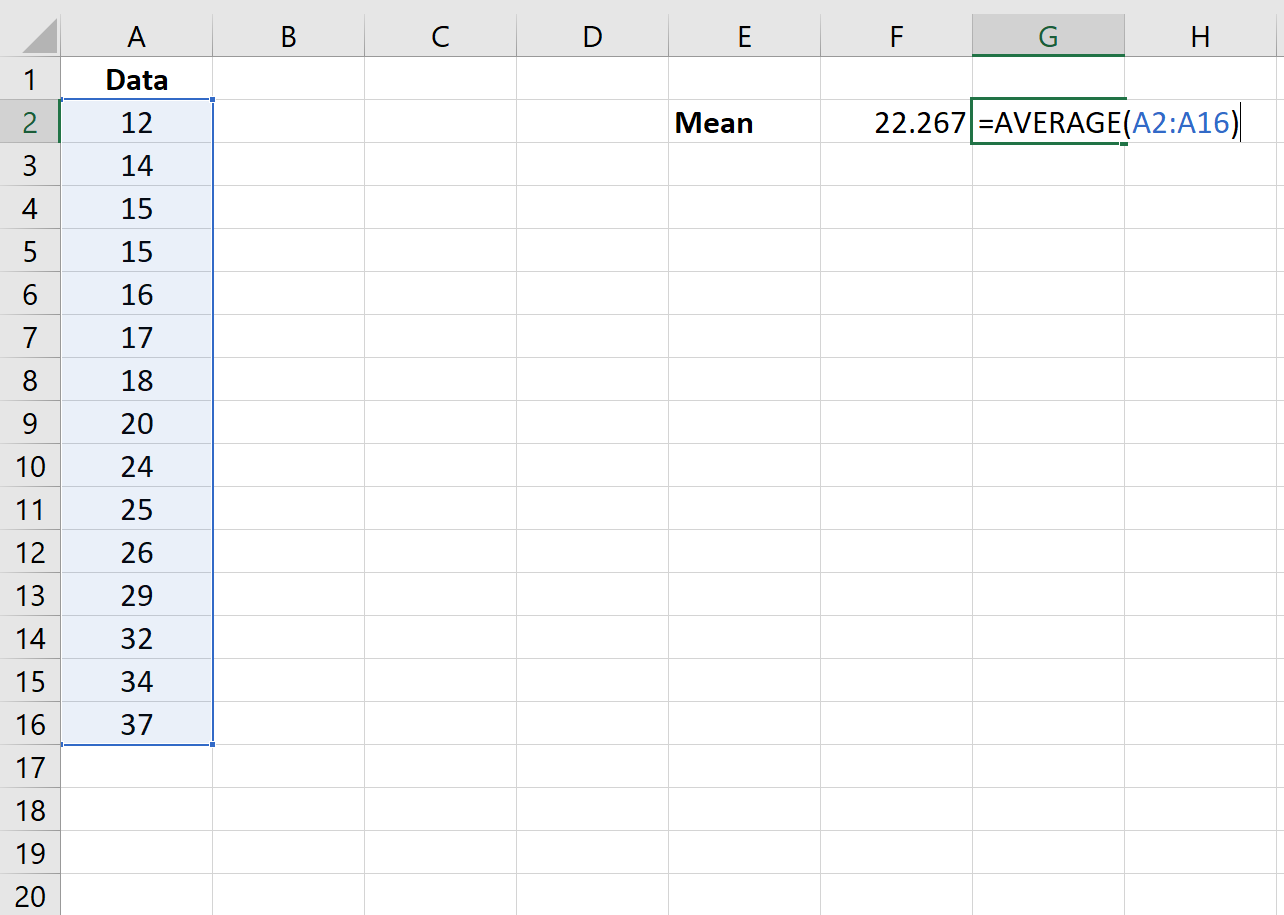
Étape 2 : Trouvez l’écart type.

Ensuite, nous utiliserons la fonction =STDEV (plage de valeurs) pour trouver l’écart type de l’ensemble de données.

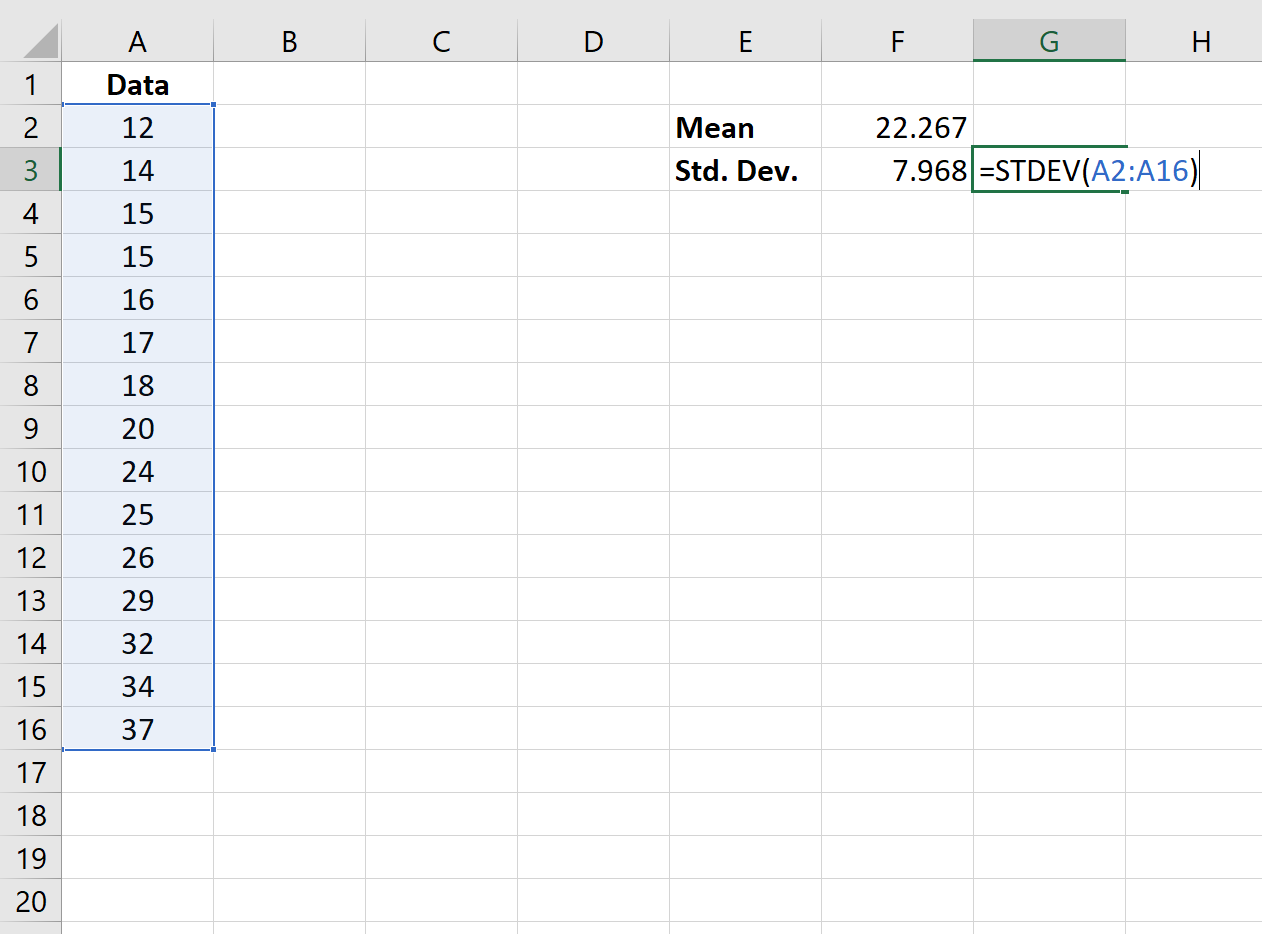
Étape 3 : Normalisez les valeurs.

Enfin, nous utiliserons la fonction STANDARDIZE(x, Mean, standard_dev) pour normaliser chacune des valeurs de l’ensemble de données.

NOTE:

La fonction STANDARDIZE utilise la formule suivante pour normaliser une valeur de données donnée :

Valeur normalisée = (x – x ) / s

où:

• x = valeur des données
• x = moyenne de l’ensemble de données
• s = écart type de l’ensemble de données

L’image suivante montre la formule utilisée pour normaliser la première valeur de l’ensemble de données :

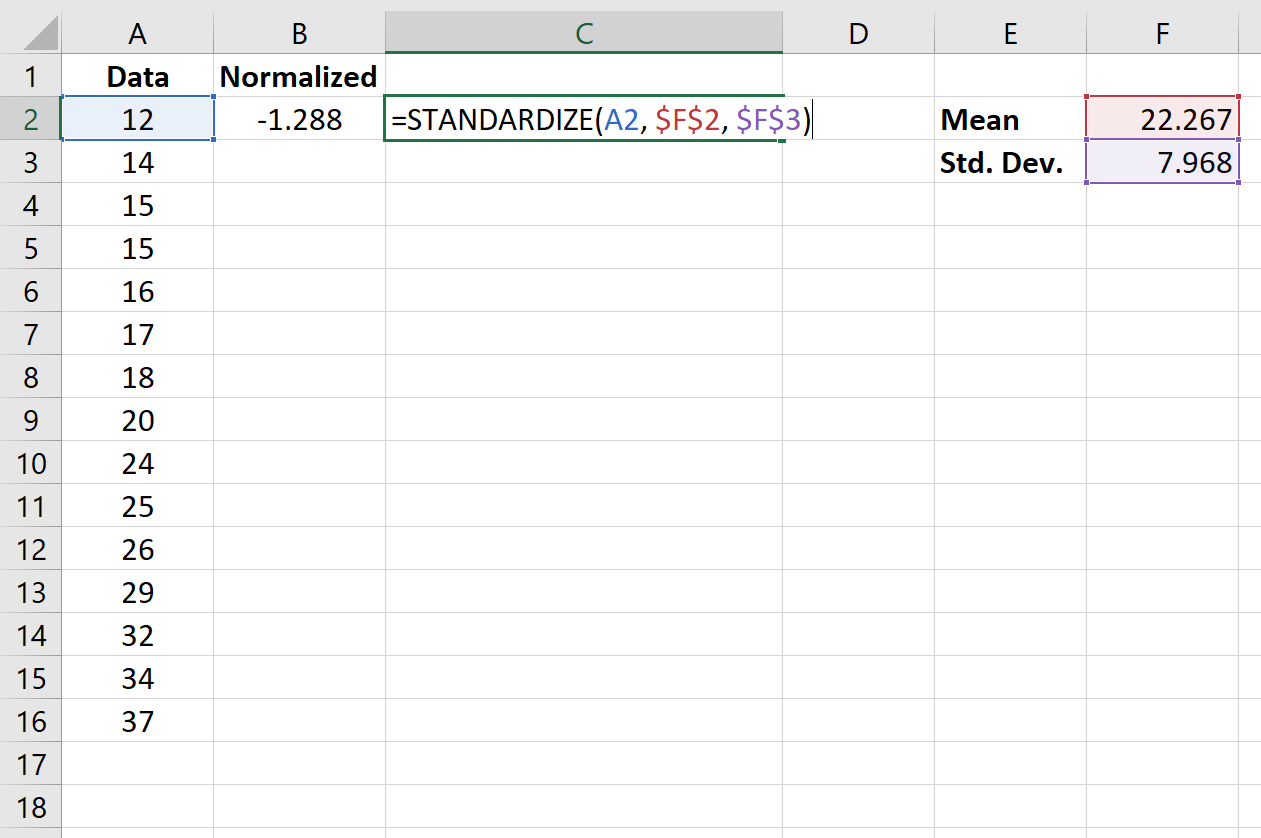
Une fois que nous avons normalisé la première valeur de la cellule B2, nous pouvons passer la souris sur le coin inférieur droit de la cellule B2 jusqu’à ce qu’un petit + apparaisse. Double-cliquez sur le + pour copier la formule dans les cellules restantes :

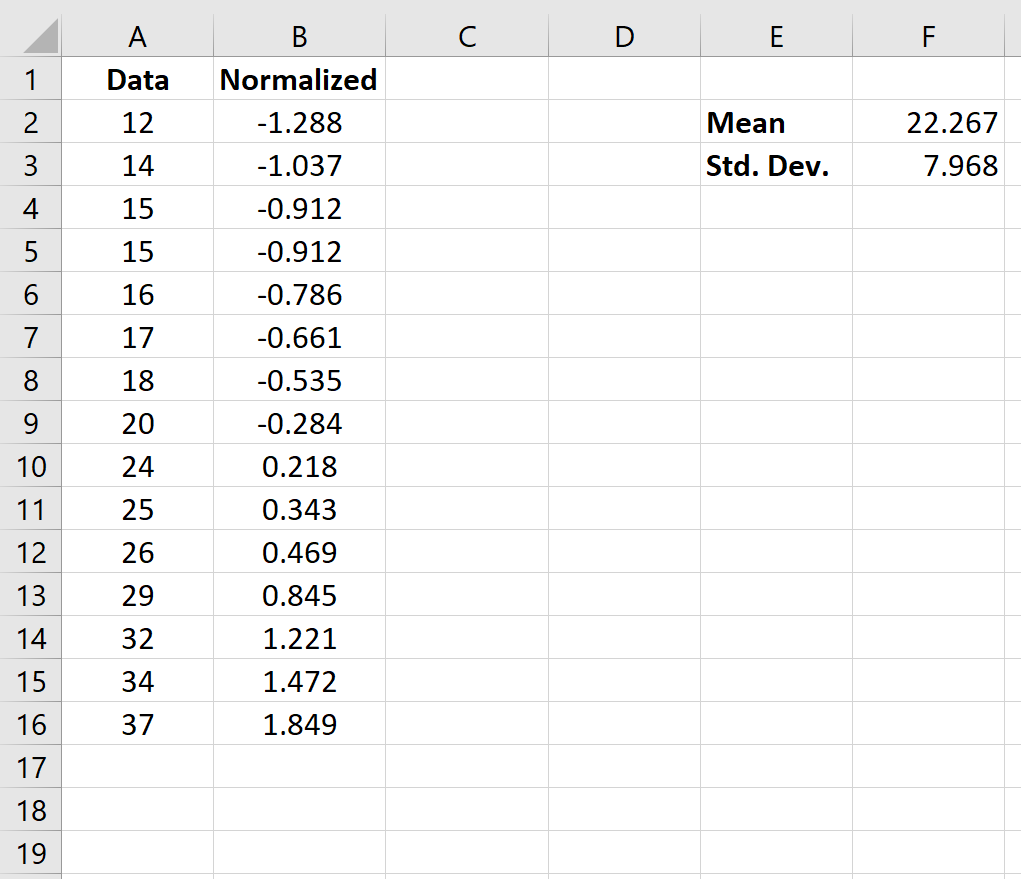
Désormais, chaque valeur de l’ensemble de données est normalisée.

Comment interpréter les données normalisées

La formule que nous avons utilisée pour normaliser une valeur de données donnée, x, était la suivante :

Valeur normalisée = (x – x ) / s

où:

• x = valeur des données
• x = moyenne de l’ensemble de données
• s = écart type de l’ensemble de données

Si un point de données particulier a une valeur normalisée supérieure à 0, cela indique que le point de données est supérieur à la moyenne. À l’inverse, une valeur normalisée inférieure à 0 indique que le point de données est inférieur à la moyenne.

En particulier, la valeur normalisée nous indique de combien d’écarts types se trouve le point de données d’origine par rapport à la moyenne. Par exemple, considérons le point de données « 12 » dans notre ensemble de données d’origine :

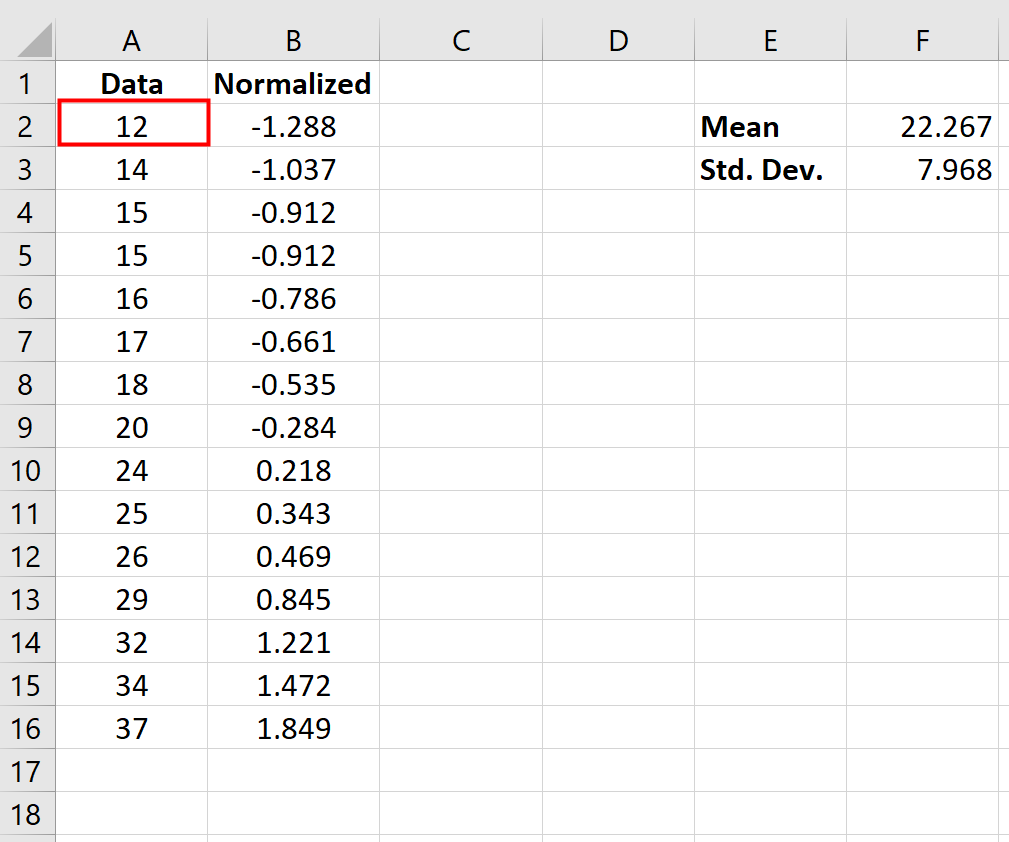
La valeur normalisée pour « 12 » s’est avérée être de -1,288, calculée comme suit :

Valeur normalisée = (x – x ) / s = (12 – 22,267) / 7,968 = -1,288

Cela nous indique que la valeur « 12 » est inférieure de 1,288 écarts-types à la moyenne de l’ensemble de données d’origine.

Chacune des valeurs normalisées de l’ensemble de données peut nous aider à comprendre à quel point une valeur de données particulière est proche ou éloignée de la moyenne. Une petite valeur normalisée indique qu’une valeur est proche de la moyenne tandis qu’une grande valeur normalisée indique qu’une valeur est éloignée de la moyenne.