Comment normaliser les données entre 0 et 100
Pour normaliser les valeurs d’un ensemble de données entre 0 et 100, vous pouvez utiliser la formule suivante :
z je = (x je – min(x)) / (max(x) – min(x)) * 100
où:
- z i : la ième valeur normalisée dans l’ensemble de données
- x i : la ième valeur de l’ensemble de données
- min(x) : La valeur minimale dans l’ensemble de données
- max(x) : La valeur maximale dans l’ensemble de données
Par exemple, supposons que nous ayons l’ensemble de données suivant :
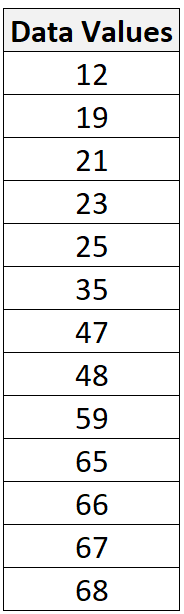
La valeur minimale dans l’ensemble de données est 12 et la valeur maximale est 68.
Pour normaliser la première valeur de 12 , nous appliquerions la formule partagée précédemment :
- z je = (x je – min(x)) / (max(x) – min(x)) * 100 = (12 – 12) / (68 – 12) * 100 = 0
Pour normaliser la deuxième valeur de 19 , nous utiliserions la même formule :
- z je = (x je – min(x)) / (max(x) – min(x)) * 100 = (19 – 12) / (68 – 12) * 100 = 12,5
Pour normaliser la troisième valeur de 21 , nous utiliserions la même formule :
- z je = (x je – min(x)) / (max(x) – min(x)) * 100 = (21 – 12) / (68 – 12) * 100 = 16,07
Nous pouvons utiliser exactement cette même formule pour normaliser chaque valeur de l’ensemble de données d’origine entre 0 et 100 :
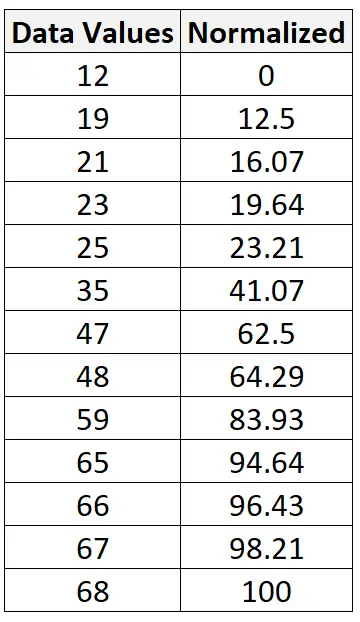
Comment normaliser les données entre n’importe quelle plage
Nous pouvons en fait utiliser cette formule pour normaliser un ensemble de données entre 0 et n’importe quel nombre :
z je = (x je – min(x)) / (max(x) – min(x)) * Q
où Q est le nombre maximum souhaité pour vos valeurs de données normalisées.
Dans l’exemple précédent, nous avons choisi Q comme étant égal à 100, mais nous pourrions facilement normaliser une plage de valeurs de données entre 0 et 1 000 en choisissant Q comme étant 1 000 :
Pour normaliser la première valeur de 12 , nous appliquerions la formule :
- z je = (x je – min(x)) / (max(x) – min(x)) * 1 000 = (12 – 12) / (68 – 12) * 100 = 0
Pour normaliser la deuxième valeur de 19 , nous utiliserions la même formule :
- z je = (x je – min(x)) / (max(x) – min(x)) * 1 000 = (19 – 12) / (68 – 12) * 100 = 125
Pour normaliser la troisième valeur de 21 , nous utiliserions la même formule :
- z je = (x je – min(x)) / (max(x) – min(x)) * 1 000 = (21 – 12) / (68 – 12) * 100 = 160,7
Nous pouvons utiliser exactement cette même formule pour normaliser chaque valeur de l’ensemble de données d’origine entre 0 et 1 000 :
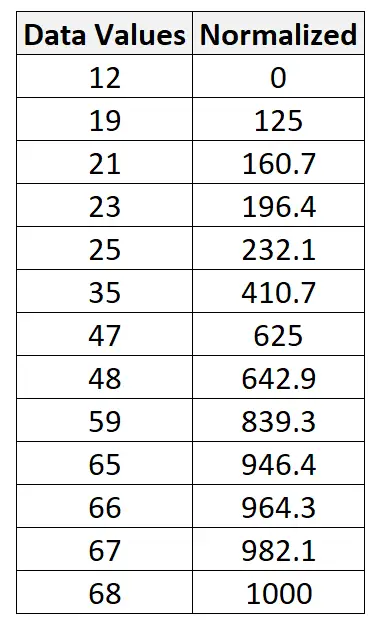
Quand normaliser les données
Parfois, nous normalisons les variables lorsque nous effectuons un certain type d’analyse dans laquelle nous avons plusieurs variables mesurées à différentes échelles et nous souhaitons que chacune des variables ait la même plage.
Cela évite qu’une variable ait une influence excessive, surtout si elle est mesurée dans des unités différentes (c’est-à-dire si une variable est mesurée en pouces et une autre en yards).
Il convient également de noter que nous avons utilisé une méthode connue sous le nom de normalisation min-max dans ce didacticiel pour normaliser les valeurs des données.
Les deux méthodes de normalisation les plus courantes sont les suivantes :
1. Normalisation Min-Max
- Objectif : Convertit chaque valeur de données en une valeur comprise entre 0 et 100.
- Formule : Nouvelle valeur = (valeur – min) / (max – min) * 100
2. Normalisation moyenne
- Objectif : met à l’échelle les valeurs de telle sorte que la moyenne de toutes les valeurs soit 0 et std. dév. est 1.
- Formule : Nouvelle valeur = (valeur – moyenne) / (écart type)
Ressources additionnelles
Comment normaliser les données entre 0 et 1
Comment normaliser les données dans Excel
Comment normaliser les données dans R
Comment normaliser les colonnes en Python
