Comment effectuer une régression OLS en Python (avec exemple)

La régression des moindres carrés ordinaires (OLS) est une méthode qui nous permet de trouver une droite qui décrit le mieux la relation entre une ou plusieurs variables prédictives et une variable de réponse .

Cette méthode nous permet de trouver l’équation suivante :

ŷ = b ₀ + b ₁ x

où:

• ŷ : La valeur de réponse estimée
• b ₀ : L’origine de la droite de régression
• b ₁ : La pente de la droite de régression

Cette équation peut nous aider à comprendre la relation entre le prédicteur et la variable de réponse, et elle peut être utilisée pour prédire la valeur d’une variable de réponse étant donné la valeur de la variable prédictive.

L’exemple étape par étape suivant montre comment effectuer une régression OLS en Python.

Étape 1 : Créer les données

Pour cet exemple, nous allons créer un ensemble de données contenant les deux variables suivantes pour 15 étudiants :

• Nombre total d’heures étudiées
• Résultat de l’examen

Nous effectuerons une régression OLS, en utilisant les heures comme variable prédictive et le score à l’examen comme variable de réponse.

Le code suivant montre comment créer ce faux ensemble de données dans les pandas :

import pandas as pd

#create DataFrame
df = pd.DataFrame({'hours': [1, 2, 4, 5, 5, 6, 6, 7, 8, 10, 11, 11, 12, 12, 14],
                   'score': [64, 66, 76, 73, 74, 81, 83, 82, 80, 88, 84, 82, 91, 93, 89]})

#view DataFrame
print(df)

    hours  score
0       1     64
1       2     66
2       4     76
3       5     73
4       5     74
5       6     81
6       6     83
7       7     82
8       8     80
9      10     88
10     11     84
11     11     82
12     12     91
13     12     93
14     14     89

Étape 2 : effectuer une régression OLS

Ensuite, nous pouvons utiliser les fonctions du module statsmodels pour effectuer une régression OLS, en utilisant les heures comme variable prédictive et le score comme variable de réponse :

import statsmodels.api as sm

#define predictor and response variables
y = df['score']
x = df['hours']

#add constant to predictor variables
x = sm.add_constant(x)

#fit linear regression model
model = sm.OLS(y, x).fit()

#view model summary
print(model.summary())

                            OLS Regression Results                            
==============================================================================
Dep. Variable:                  score   R-squared:                       0.831
Model:                            OLS   Adj. R-squared:                  0.818
Method:                 Least Squares   F-statistic:                     63.91
Date:                Fri, 26 Aug 2022   Prob (F-statistic):           2.25e-06
Time:                        10:42:24   Log-Likelihood:                -39.594
No. Observations:                  15   AIC:                             83.19
Df Residuals:                      13   BIC:                             84.60
Df Model:                           1                                         
Covariance Type:            nonrobust                                         
==============================================================================
                 coef    std err          t      P>|t|      [0.025      0.975]
------------------------------------------------------------------------------
const         65.3340      2.106     31.023      0.000      60.784      69.884
hours          1.9824      0.248      7.995      0.000       1.447       2.518
==============================================================================
Omnibus:                        4.351   Durbin-Watson:                   1.677
Prob(Omnibus):                  0.114   Jarque-Bera (JB):                1.329
Skew:                           0.092   Prob(JB):                        0.515
Kurtosis:                       1.554   Cond. No.                         19.2
==============================================================================

À partir de la colonne coef , nous pouvons voir les coefficients de régression et écrire l’équation de régression ajustée suivante :

Score = 65,334 + 1,9824*(heures)

Cela signifie que chaque heure supplémentaire étudiée est associée à une augmentation moyenne de la note à l’examen de 1,9824 points.

La valeur d’origine de 65,334 nous indique la note moyenne attendue à l’examen pour un étudiant qui étudie zéro heure.

Nous pouvons également utiliser cette équation pour trouver la note attendue à l’examen en fonction du nombre d’heures qu’un étudiant étudie.

Par exemple, un étudiant qui étudie pendant 10 heures devrait obtenir une note à l’examen de 85,158 :

Note = 65,334 + 1,9824*(10) = 85,158

Voici comment interpréter le reste du résumé du modèle :

• P(>|t|) : Il s’agit de la valeur p associée aux coefficients du modèle. Puisque la valeur p pour les heures (0,000) est inférieure à 0,05, nous pouvons dire qu’il existe une association statistiquement significative entre les heures et le score .
• R au carré : cela nous indique que le pourcentage de variation des résultats de l’examen peut s’expliquer par le nombre d’heures étudiées. Dans ce cas, 83,1 % de la variation des scores peut être expliquée par les heures étudiées.
• Statistique F et valeur p : La statistique F ( 63,91 ) et la valeur p correspondante ( 2,25e-06 ) nous indiquent la signification globale du modèle de régression, c’est-à-dire si les variables prédictives du modèle sont utiles pour expliquer la variation. dans la variable de réponse. Étant donné que la valeur p dans cet exemple est inférieure à 0,05, notre modèle est statistiquement significatif et les heures sont considérées comme utiles pour expliquer la variation du score .

Étape 3 : Visualisez la ligne la mieux adaptée

Enfin, nous pouvons utiliser le package de visualisation de données matplotlib pour visualiser la ligne de régression ajustée sur les points de données réels :

import matplotlib.pyplot as plt

#find line of best fit
a, b = np.polyfit(df['hours'], df['score'], 1)

#add points to plot
plt.scatter(df['hours'], df['score'], color='purple')

#add line of best fit to plot
plt.plot(df['hours'], a*df['hours']+b)

#add fitted regression equation to plot
plt.text(1, 90, 'y = ' + '{:.3f}'.format(b) + ' + {:.3f}'.format(a) + 'x', size=12)

#add axis labels
plt.xlabel('Hours Studied')
plt.ylabel('Exam Score')

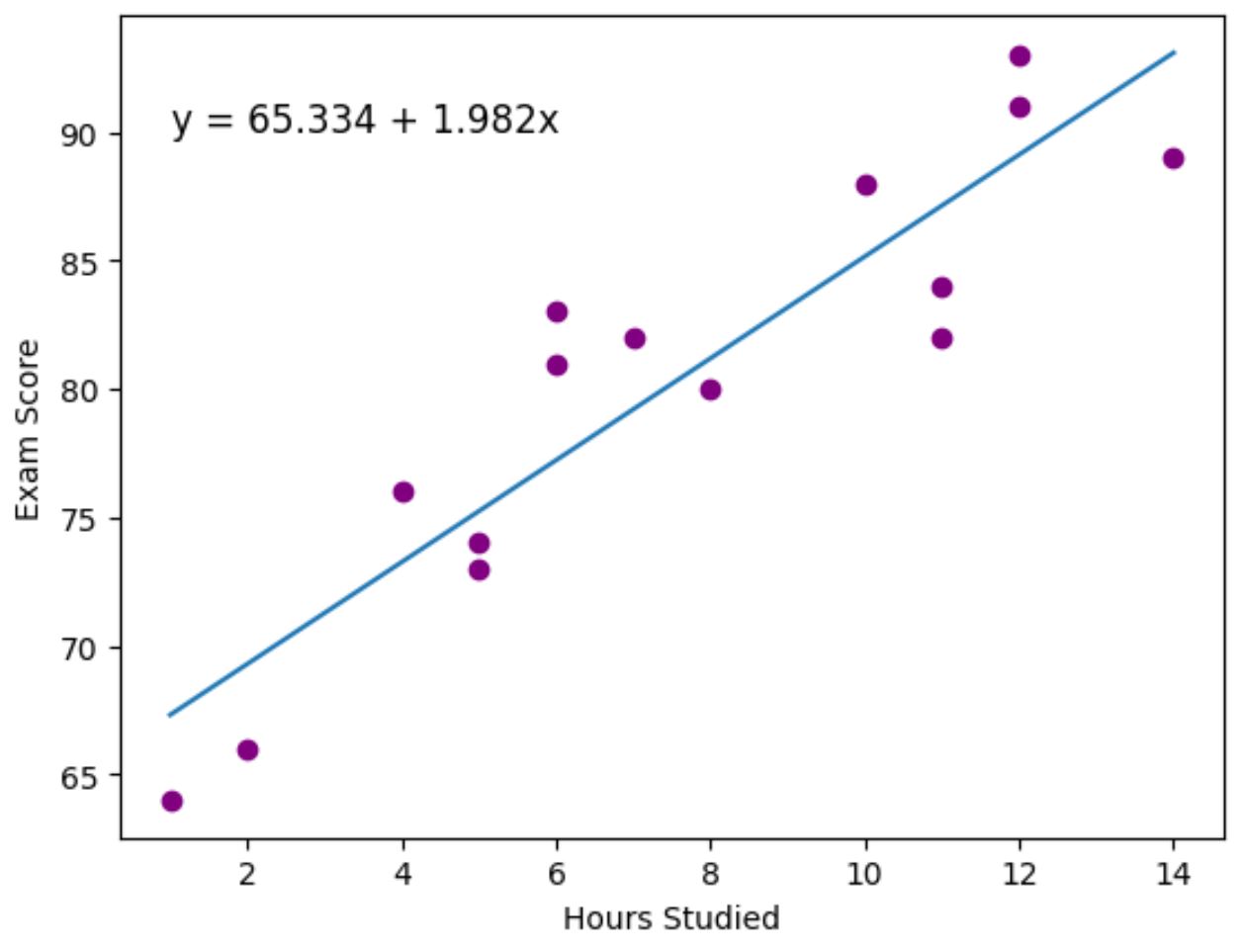
Les points violets représentent les points de données réels et la ligne bleue représente la ligne de régression ajustée.

Nous avons également utilisé la fonction plt.text() pour ajouter l’équation de régression ajustée dans le coin supérieur gauche du tracé.

En regardant le graphique, il semble que la droite de régression ajustée capture assez bien la relation entre la variable des heures et la variable du score .

Ressources additionnelles

Les didacticiels suivants expliquent comment effectuer d’autres tâches courantes en Python :

Comment effectuer une régression logistique en Python
Comment effectuer une régression exponentielle en Python
Comment calculer l’AIC des modèles de régression en Python