Comment effectuer une ANOVA unidirectionnelle dans Excel

Une ANOVA unidirectionnelle (« analyse de variance ») est utilisée pour déterminer s’il existe ou non une différence statistiquement significative entre les moyennes de trois groupes indépendants ou plus.

Ce didacticiel explique comment effectuer une ANOVA unidirectionnelle dans Excel.

Exemple : ANOVA unidirectionnelle dans Excel

Supposons qu’un chercheur recrute 30 étudiants pour participer à une étude. Les étudiants sont assignés au hasard à utiliser l’une des trois techniques d’étude au cours des trois semaines suivantes pour se préparer à un examen. A la fin des trois semaines, tous les étudiants passent le même test.

Les résultats des tests des étudiants sont indiqués ci-dessous :

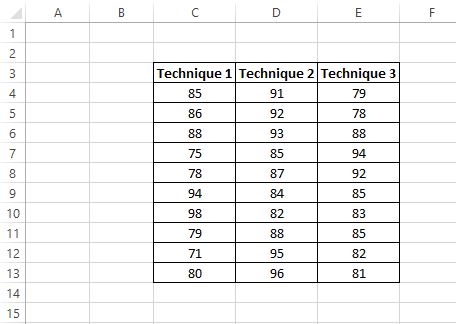
Le chercheur souhaite effectuer une ANOVA unidirectionnelle pour déterminer si les scores moyens sont les mêmes dans les trois groupes.

Pour effectuer une ANOVA unidirectionnelle dans Excel, accédez à l’onglet Données , puis cliquez sur l’option Analyse des données dans le groupe Analyse .

Si vous ne voyez pas l’option Data Analysis , vous devez d’abord charger le logiciel gratuit Analysis ToolPak .

Une fois que vous avez cliqué dessus, une fenêtre apparaîtra avec différentes options d’outils d’analyse. Sélectionnez Anova : facteur unique , puis cliquez sur OK .

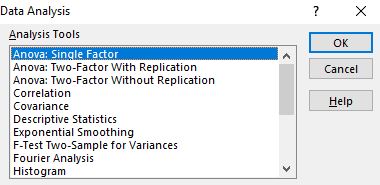
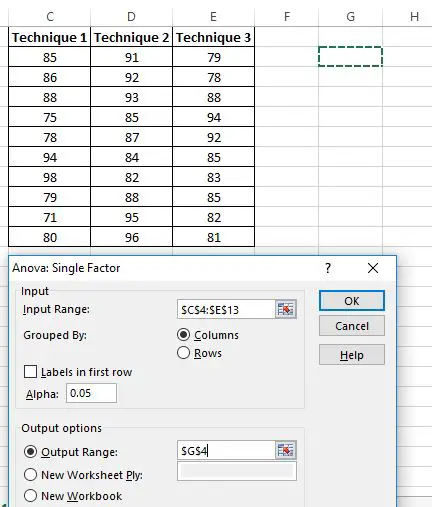
Une nouvelle fenêtre apparaît demandant une plage d’entrée . Vous pouvez soit faire glisser un cadre autour de vos données, soit saisir manuellement la plage de données. Dans ce cas, nos données se trouvent dans les cellules C4:E13 .

Ensuite, choisissez un niveau Alpha pour le test. Par défaut, ce nombre est 0,05. Dans ce cas, je le laisserai à 0,05.

Enfin, choisissez une cellule pour la plage de sortie , où apparaîtront les résultats de l’ANOVA unidirectionnelle. Dans ce cas, je choisis la cellule G4 .

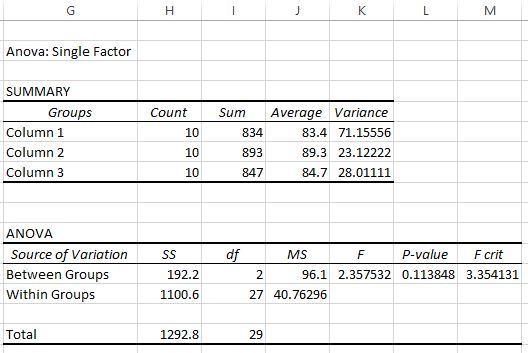
Une fois que vous avez cliqué sur OK , le résultat de l’ANOVA unidirectionnelle apparaîtra :

Interprétation du résultat

Deux tableaux sont affichés dans la sortie. Le premier est un tableau récapitulatif qui montre le nombre de résultats aux tests dans chaque groupe, la somme des résultats aux tests, la moyenne des résultats aux tests et la variance des résultats aux tests.

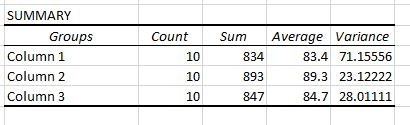
Rappelons qu’une ANOVA unidirectionnelle est utilisée pour déterminer s’il existe ou non une différence statistiquement significative entre les moyennes de trois groupes ou plus.

À partir de ce premier tableau, nous pouvons voir que le score moyen pour chacun des trois groupes est différent, mais pour savoir si ces différences sont statistiquement significatives, il faut regarder le deuxième tableau.

Le deuxième tableau montre la statistique du test F, la valeur critique F et la valeur p :

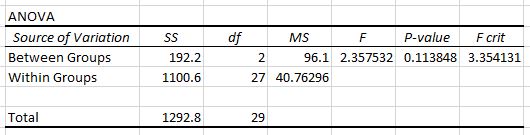
Dans ce cas, la statistique du test F est de 2,3575 et la valeur critique de F est de 3,3541 . Étant donné que la statistique du test F est inférieure à la valeur critique de F, nous ne disposons pas de preuves suffisantes pour rejeter l’hypothèse nulle selon laquelle les moyennes des trois groupes sont égales.

Cela signifie que nous ne disposons pas de preuves suffisantes pour affirmer qu’il existe une différence dans les résultats des tests entre les trois techniques d’étude.

Nous pourrions également utiliser la valeur p pour parvenir à la même conclusion. Dans ce cas, la valeur p est de 0,1138 , ce qui est supérieur au niveau alpha de 0,05 .

Cela signifie que nous ne disposons pas de preuves suffisantes pour rejeter l’hypothèse nulle selon laquelle les moyennes des trois groupes sont égales.

Remarque : Dans les cas où vous rejetez l’hypothèse nulle, vous pouvez effectuer un test post hoc de Tukey-Kramer pour déterminer exactement quelles moyennes de groupe sont différentes.